一类超前型泛函微分方程振动性的比较定理

双瑞涛，秦宏立

(延安大学 数学与计算机科学学院，陕西 延安 716000)

1 引言

众所周知，在现代生物学、经济学和人工神经网络动力学中，泛函微分方程的振动理论是不可或缺的，广泛的应用背景引起了许多学者对其进行探索研究，从而得到了一些重要的结果。例如，在文献［1］中Ladas和Stavoulakis证明了若方程

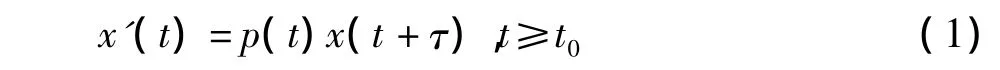
(其中 p(t)∈C(R+to，R+)，τ＞0 为常数，R+to:=［t0，+∞)，R+:=［0，+∞)满足条件

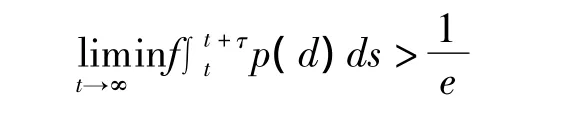
则方程(1)式的所有解振动;当p(t)≡p∈(0，+∞)时，Kusano在文献［2］中得出

是方程(1)式只有振动解的充要条件。文献［3］的作者运用构造函数序列{pn(t)}、{qn(t)}的方法，得到方程(1)式振动的“sharp”条件，即如果存在t1＞t0+τ及正整数k使得

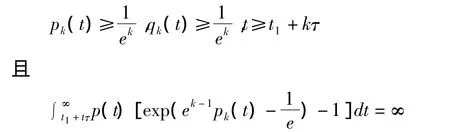
那么，方程(1)式是解振动的;并通过具体例子验证所给结果的有效性。

本文讨论一类变滞量的超前型泛函微分方程

(其中 p(t)，τ(t)∈C(R+，R+))的振动性问题。首先建立关于方程(2)式的振动性比较定理，然后应用比较定理得到了方程(2)式振动的充分性条件，并且当p(t)，τ(t)为常数时，这些条件也是必要的。

如通常定义，如果方程(2)的一个非零解x(t)有任意大的零点，则称解x(t)为振动的;若它最终为正或最终为负，则称其为非振动的。若方程(2)的所有解都是振动的，则称方程(2)是振动的;否则，称其为非振动的。

2 主要结果

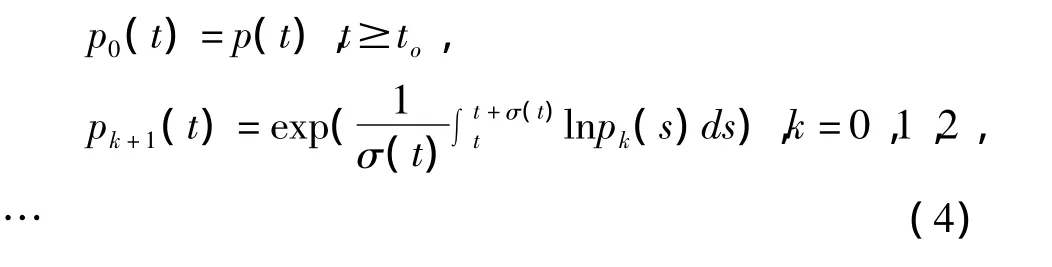
首先，建立方程(2)式与方程

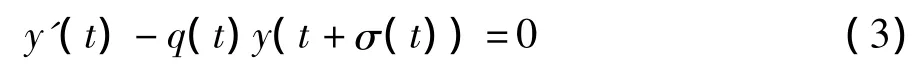
(其中q(t)σ(t)∈C(R+，R+))之间的振动性比较定理。

设t0≥0为一给定的实数，令

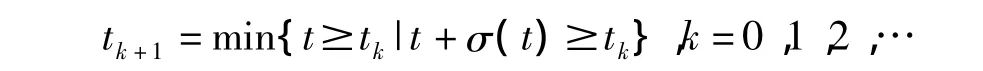
显然，tk+1≥tk≥t0，k=0，1，2…．

假设 t≥t0时 p(t)＞0，σ(t)＞0，并定义

易知，函数pk(t)在［tk，+∞)上有定义、连续且pk(t)＞0，t≥tk，k=0，1，2，…．

定理1 设存在某个实数t0≥0及正整数n＞0，使得

(ⅰ)σ(t)在［t0，+∞)上非减;

(ⅱ)当 t≥t0时，σ(t)≤τ(t);

(ⅲ)当 t≥t0时，q(t)≤pn(t)．

那么，若方程(3)式振动，则方程(2)式也振动．

证明:采用反证法．假设方程(2)式有最终正解x(t)，取充分大的 T0≥t0，使 t≥T0时

x(t)＞0，x(t+τ(t))＞0

则有 x'(t)＞0，t≥T0记

TK+1=min{t≥Tk|t+σ(t)≥Tk}，k=0，1，2…显然，0≤T0≤T1≤…≤Tk≤Tk+1→∞ (t→∞ )，且 Tk≥tk，k=0，1，2，…．令

由于，函数λk(t)在［Tk，+∞)上有定义、连续且 λk＞0，t≥Tk，k=0，1，2，…．从而，利用积分的定义及平均不等式［4］，即

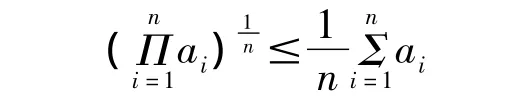
(其中 ai＞0，i=1，2，…，n)，当 t≥Tk时，由(6)式得

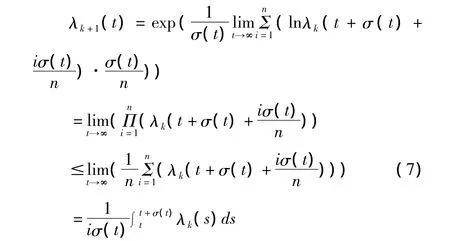
对于一切 k=0，1，2，…成立。

取 T*1=min{t≥T0|t+ τ(t)≥To}，易见 T*1≥T1．设 t≥T*1，则 t+ τ(t)≥T0．将(5)式两边同时从 t到 t+τ(t)积分，得

将(5)与(8)式代入方程(2)式，整理得

注意到 p(t)=p(t)，t≥t 及条件(ⅱ)，则有

上式两端同时取对数，有

再由(7)式知

利用(4)式和(6)式，上式可写为

其中n如命题条件中所示。定义函数集

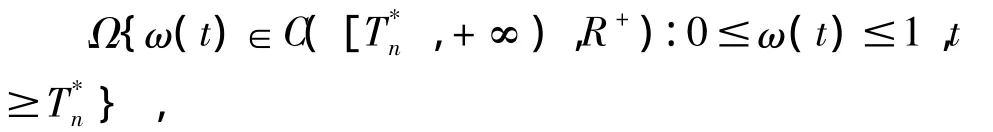
并在Ω上定义映射

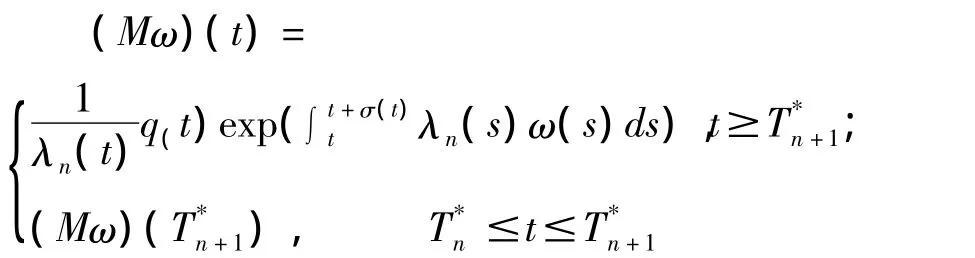
则对任何ω(t)∈Ω及t≥T*n+1，由条件(ⅲ)和(10)式知

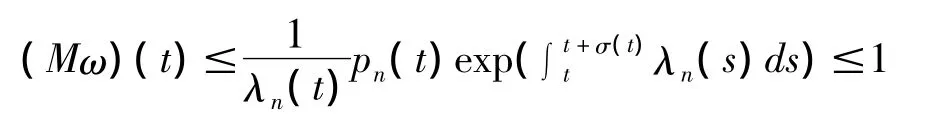
这意味着M映入Ω其自身。现在Ω中作函数列{ω (t)}如下:

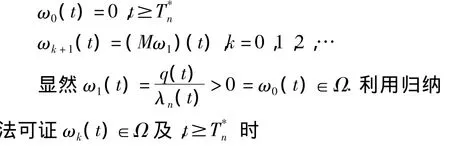
对一切成立。于是存在极限

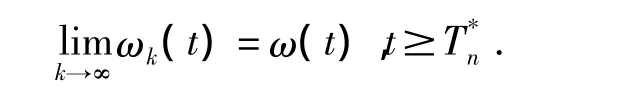
由Lebesgue控制收敛定理［5］知，ω是在Ω中的一个不动点，(Mω)(t)=ω(t)，即

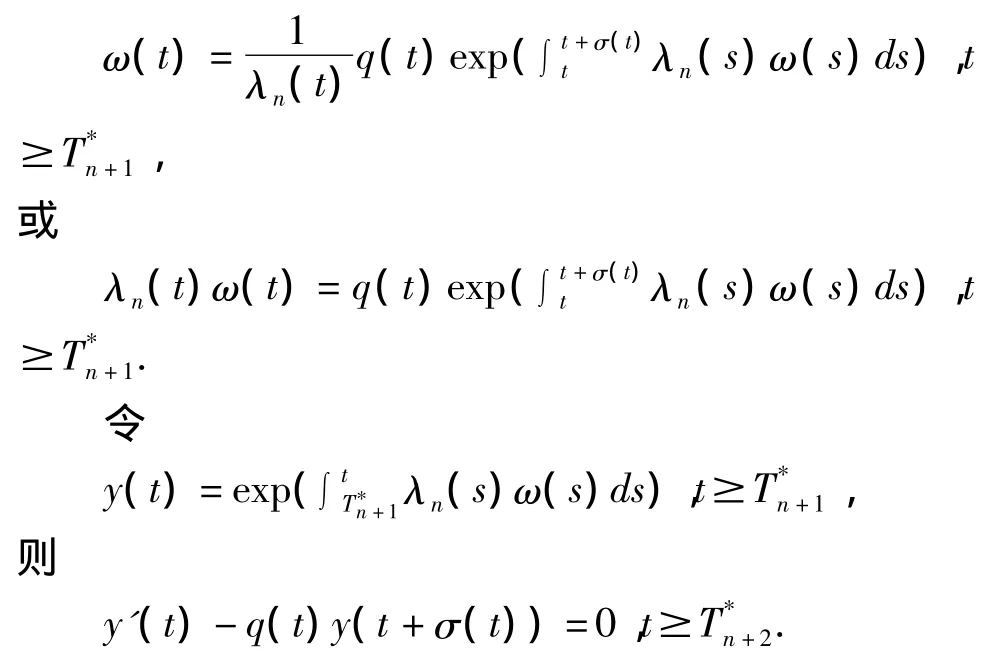
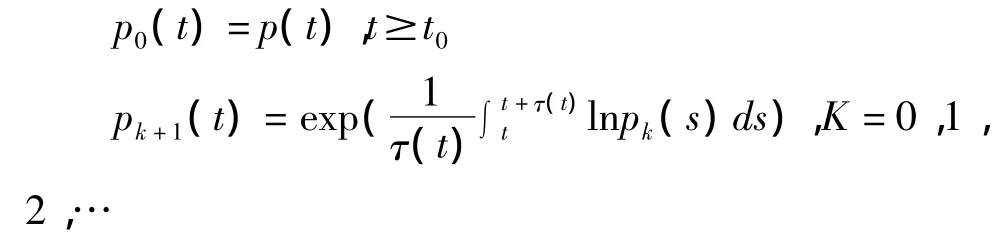
即y(t)是方程(3)式的一个正解，这与方程(3)式振动矛盾，因此假设不成立。故方程(2)式是振动的。证毕

在下面的讨论中，我们总假设当t≥t0≥0时，p(t)＞0，τ(t)＞0。令

则由定理1我们有下面两个推论，即

推论1 若τ(t)非减，且对某个正整数n＞0，方程振动，则方程(2)也振动。

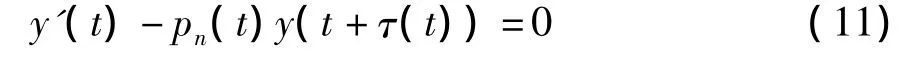
推论2 若τ(t)非减，且对某个正整数n＞0，使得

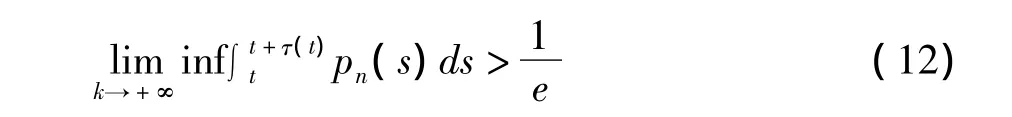
则方程(2)振动。

注:当p(t)=p，τ(t)= τ都是正常数时，(12)式退化为 pτ＞，这是大家熟知的使方程(1)(或

(2))振动的充要条件。

［1］Ladas G，Stavroulakis I P．Oscillations caused by several retarded and advanced arguments［J］．J Diff Eqs，1982，44:134－152．

［2］Kusano T．On even order functional differential equation with advanced and retarded arguments［J］．J Diff Eqs，1982，45:75－84．

［3］秦宏立．一类AFDE的振动性及其应用［J］．西南民族大学学报，2010，36(6):885 －889．

［4］魏俊杰．一阶偏差变元微分方程振动的充要条件及应用［J］．数学学报，1989，32(5):632 －638．

［5］Huang Q G．Comparison theorems for first order retarded functions［J］．J Diff Integal Eqs，1991(4):1101 － 1112．