游程理论下生灭过程的构造

吕 芳， 王 燕

(洛阳师范学院 数学科学学院 河南 洛阳 471022)

0 引言

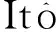
1 基本假定及记号

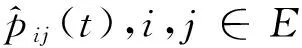
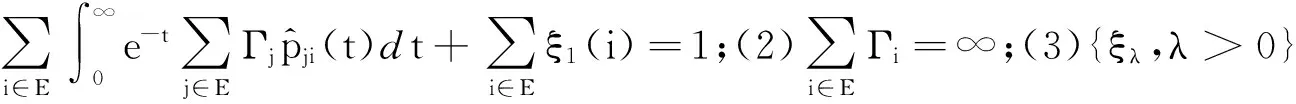
从而，对任意的λ>0,ξλ满足方程组ξλ(λI-Q)=0(其中I为单位矩阵).

令EΔ=E∪{∞}为E的一点紧化. 令U={w:(0,∞)→EΔ;且∃s>0,使得w(s)∈E;若w(u)=∞,则对任意v>u,w(v)=∞}.U上的坐标过程记作{c(t)}t>0，由坐标过程产生的σ代数σ{c(t),t>0}记作U0，σ{c(s),s≤t}记作Ut.令σ∞=inf{t>0,c(t)=∞}表示游程的生存时间.

2 过程的构造

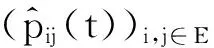
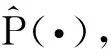
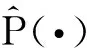
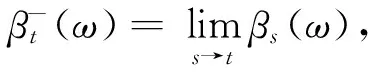
对于任意的λ>0,x∈EΔ，有

从而，对于任意的λ>0,x∈EΔ,有

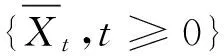
则{Xt,t≥0}是一个取值于EΔ的过程，且它的所有轨道右连续.

3 确定过程的游程系

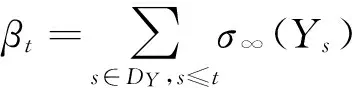
定理2对于任意的λ>0,i,j∈E，有

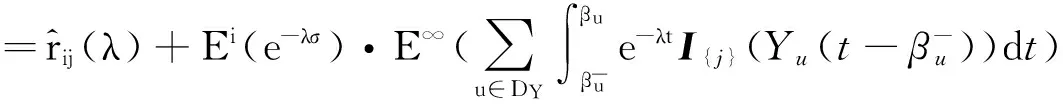
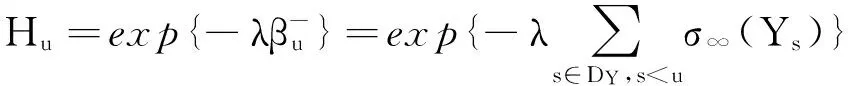
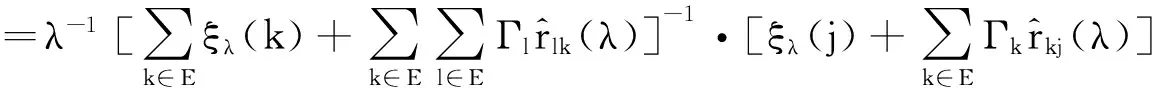
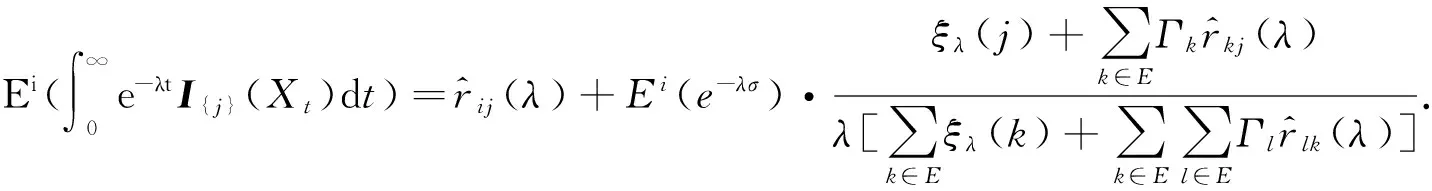
定理3{rij(λ);i,j∈E}是一个预解式.即{rij(λ);i,j∈E}满足

证明1)由于

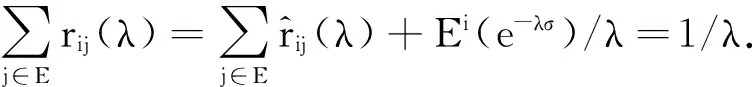
3)由于

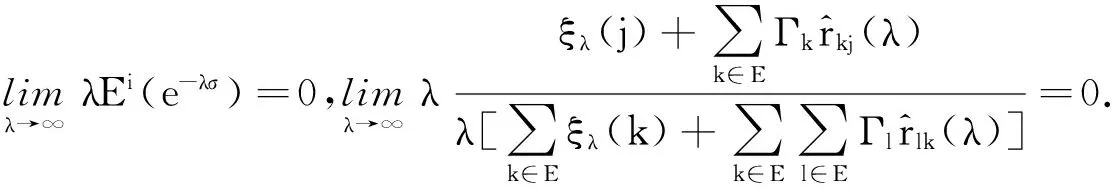
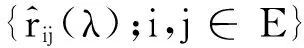
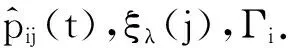
参考文献：

[1] 王梓坤.随机过程通论[M]. 北京：北京师范大学出版社,1996.

[2] 朱全新,舒小保.两类生灭过程的特征数及其概率意义[J].高校应用数学学报,2006,21(3):311-320.

[3] 朱全新,戴永隆.以0为飞射壁的生灭过程爆发前的若干性质[J].数学物理学报,2007,27(A)(3):456-469.

[4] 吴群英,林亮.全稳定广义生-灭最小Q过程的构造[J].广西科学,2005,12(1):10-13.

[5] 朱全新,杨向群.以0为反射壁和拟飞射壁的生灭过程爆发前的向下性质[J].应用概率统计, 2005,21(2) :188-196.

[7] 王梓坤,杨向群.生灭过程与马尔可夫链[M]. 北京：科学出版社,1980.

[8] Nobuyuki, Shinzo W. Stochastic Differential Equations and Diffusion Processes[M]. New York :North-Holland Publish Company,1989.

[9] J Bertoin J. Levy Processes[M]. Cambridge:Cambridge University Press,1996.