介质中的电磁能量密度及其损耗
2012-05-22韩光泽朱小华
韩光泽 朱小华
(华南理工大学 物理系 广东 广州 510640)
0 引言
频率在300 MHz~300 GHz之间的微波段电磁波广泛用于无线通信、材料处理、微波加热、化工过程强化和医疗诊断等领域.电磁技术的进一步广泛应用需要对电磁场与物质相互规律的深入了解,尤其是物质对电磁波的吸收与消耗.例如,用于通信的电磁波应尽可能避免被介质吸收,用于材料处理和加热时应使物质尽可能多的吸收电磁波,而在强化质量传递过程时需要使某一特定的组分尽可能多的吸收电磁波[1-3].由于电磁场与物质相互作用的特殊性和复杂性,这种作用的某些物理机制仍然不是很清楚.在电磁场与物质相互作用的基础理论方面,电磁场能量被物质的吸收与消耗显得尤为重要.但是,目前关于物质中的电磁能量形式以及物质对电磁场能量的储存与吸收消耗等方面物理机理的认识不太明确,能量的数学表述形式也不太确切.本文将以电磁场理论为基础,基于电磁介质在电磁场中的极化和磁化特性,分析电磁介质中的电磁能量特征,导出极化能量密度和磁化能量密度表达式;并进一步研究电磁介质对电磁能量消耗的机理,导出介质吸收电磁能量的数学表达式.
1 介质中的电场能量密度和磁场能量密度
1.1 电磁能量密度
电磁场的能量特性通常采用能量密度w和能流密度S来描述.电磁场的能量平衡方程是[4]
-
(1)
设介质中的电荷密度是ρe,电荷的运动速度是v,单位体积介质受到的电磁作用力(洛伦兹力)密度是fe=ρeE+ρev×B,其中E和B分别是电场强度和磁感应强度.电磁场对运动电荷做的功率密度为
fe·v=ρev·E=Je·E,
(2)
其中Je=ρev是电流密度.
电场对电介质的作用效果是产生极化电荷和极化电流,极化电荷密度是ρp=-·P,极化电流密度是Jp=∂P/∂t,P是极化强度,即单位体积介质中的电偶极矩.磁场对磁介质的磁化效果是产生磁化电流,磁化电流密度是Jm=×M,M是磁化强度,即单位体积介质中的磁偶极矩.在定义了两个辅助量,电位移D=ε0E+P和磁场强度H=B/μ0-M后,麦克斯韦方程中只出现自由电荷和自由电流.式(2)中的Je可视为自由电荷流密度Jf,利用介质中的麦克斯韦方程组将Jf·E表示为场量,再与平衡方程(1)式比较,可分别定出能流密度S=E×H和能量密度的表达式[4]
(3)
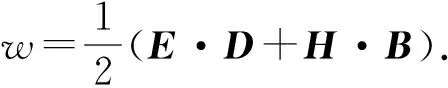
1.2 极化能量密度和磁化能量密度
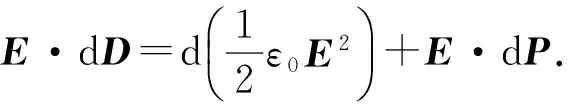
dwp=E·dP,
(4)
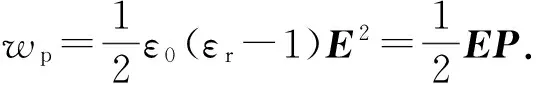
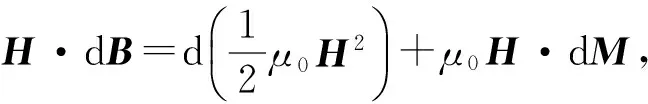
dwm=μ0H·dM.
(5)
在各向同性非铁磁物质中有M=(μr-1)H,可得dwm=μ0HdM,μ0和μr分别是真空中的磁导率和表示磁介质性质的相对磁导率.2种分解只相差一个全微分,因此这2种表达式在热力学分析中是等价的[6].
1.3 极化能和磁化能的物理意义
在导出式(3)的过程中,将介质与电磁场合并在一起作为研究的系统,而将自由电荷和自由电流作为外界,通过外界与系统之间的能量交换导出能量密度和能流密度.也可以从另一方面考虑,即将电磁场作为研究的系统,通过电磁场与介质、自由电荷和自由电流之间相互作用引起的能量交换来导出能量密度.如果只选取电磁场作为研究的系统,在电磁场与外界的作用中,功率密度式(2)中的电流密度应该包括自由电流密度、极化电流密度和磁化电流密度
Je·E=Jf·E+Jp·E+Jm·E,
(6)
由于电磁场与介质之间的相互作用而储存在介质中的能量可以通过式(6)的右侧分别导出.当介质中存在自由电荷时,Jf·E表示电磁场对自由电荷做功,通过做功电磁场的能量转换为自由电荷的动能.由于介质电阻的作用,由欧姆定律Jf=σE得
Jf·E=σE2,
(7)
这就是焦耳定律,即由于电阻的作用,电磁场对自由电荷做的功转换为焦耳热.式(7)就是这种发热功率密度,其中的σ表示介质的电导率.式(6)右侧的第2项表示电场使介质极化时所做的功率密度,通过这个功,电磁场的能量转化为介质中的极化能.利用极化电流密度表达式Jp=∂P/∂t,可得极化能量密度Jp·Edt=E·dP,这正是式(4).式(6)右侧的第3项表示电磁场使介质磁化时所做的功率密度,通过这个功,电磁场的能量转化为介质中的磁化能.利用磁化电流密度的表达式,也可得到磁化能量密度式(5).
储存在介质中的电磁能量密度来自电场做的极化功和磁场做的磁化功,因此也可以从微观的角度,利用电磁场对电偶极子和磁偶极子做功导出式(4)和式(5).电场对电介质的极化分为有极分子的取向极化和无极分子的位移极化.以位移极化为例,利用电偶极子的定义p=ql,电场极化单个分子做的功是F·dl=qE·dl=E·dp.将该式对单位体积介质内所有的电偶极子求和,并利用极化强度的定义P=∑pi,即得单位体积内电场做的总极化功E·dP.磁场对非铁磁介质的磁化也分为2类,顺磁质分子固有磁矩沿外场方向的排列和抗磁质分子产生感生磁矩.以顺磁质分子的磁化为例,设分子的固有磁矩是m,分子在磁场中受到的力矩是μ0Hmsinθ,则根据功能原理,磁化能量的增加等于磁场迫使磁偶极子转动过程中磁力矩做的负功,-μ0Hmsinθdθ=μ0Hd(mcosθ)=μ0H·dm,式中的θ表示m与H之间的夹角.在单位体积内对该式求和,并利用磁化强度的定义M=∑mi,即得磁化功μ0H·dM.
2 交变外场作用下的电磁能量损耗
在交变外场中,储存在介质中的极(磁)化能量可以还原为电(磁)场能量,也就是说,场能与介质中的极(磁)化能可以发生相互转换.依据介质的性质,这些转换有些是可逆的,有些是不可逆的,即在某一些介质中电磁能量被不可逆地转化为介质的热能.电磁波的传播损失、微波能的利用等都与电磁能量损耗相关,它同时也是电磁介质非平衡态热力学分析的基础.
2.1 各向同性单值介质
在各向同性的介质中,E、D和P具有相同的方向,B、H和M具有相同的方向(反磁质相反,由μr的取值决定),可以不考虑这些物理量的方向.如果在某种介质中P与E、M与H之间有单值对应关系,称这种介质为单值介质.线性介质就是单值对应关系的一个特例.
分别对式(4)和式(5)积分,可得介质中的极化能量密度和磁化能量密度
(8)
(9)
这2个积分式表明,如果以外场E(或H)为自变量,P(或M)为函数画一坐标曲线P(E)(或M(H)),则介质中的能量密度等于曲线与P轴(或M轴)所包围的面积.
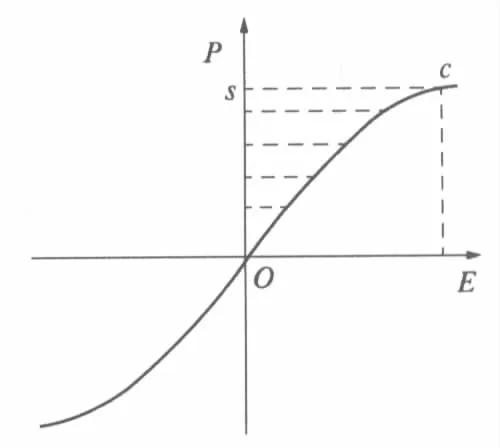
图1 单值电介质中极化强度随交变电场的变化关系Fig.1 Relationship between polarization of single-value dielectric and electric field
设P与E之间有简单的单值对应关系,P=ε0(εr-1)E,如图1所示.当场强正向(E>0)增加时,沿曲线从O点到c点,介质的极化强度随之增加dP>0,EdP>0;表示电场对介质做功,电场能量转换为介质中的极化能量,极化能量密度增加,增加的能量密度等于图形OcsO包围的面积.当场强从正向(E>0)减小时,沿曲线从c点回到O点,极化强度也减小dP<0,EdP<0;表示介质对电场做功,介质中的极化能转换为电场能,减少的能量密度也等于图形OcsO的面积.场强在反方向(E<0)由增大到减小的变化中,能量的变化关系与正向类似.因此在电场的一个变化周期内,电场对介质做的功等于介质对电场做的功,储存在介质中的极化能与电场能等量地相互转换,介质没有消耗电场能量.在电场的一个变化周期内,式(8)的积分等于零∮EdP=0.
设电场按简谐规律变化E=E0cosωt,则在线性介质中极化强度可写为P=P0cosωt,E0和P0表示场强和极化强度的峰值,ω=2π/T表示角频率,T是周期.场强和极化强度随时间变化的曲线如图2所示.在第1个1/4周期内(Ⅰ区),E>0,dP<0,因此EdP<0,表示介质对电场做功,极化能转换为电场能,介质中的极化能量密度减少.在第2个1/4周期内(Ⅱ区),E<0,dP<0,EdP>0,表示电场对介质做功,介质中的极化能量密度增加.在Ⅲ区有EdP<0,Ⅳ区有EdP>0.即在Ⅰ区和Ⅲ区介质对电场做功,介质中的极化能转化为电场能;在Ⅱ区和Ⅳ区电场对电介质做功,电场能转化为介质中的极化能.由图线的对称性可知,在电场的一个变化周期内,介质对电场做的功等于电场对介质做的功.虽然介质和电场不断交换能量,但介质从电场中吸收的能量等于交还给电场的能量,介质中没有出现极化能量的损耗.
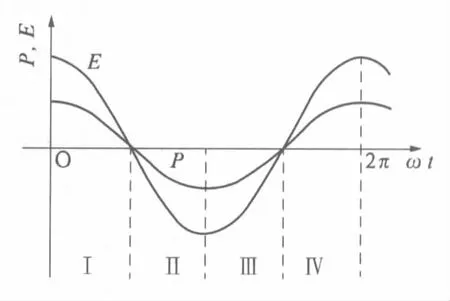
图2 线性电介质中简谐电场和极化强度随时间的变化关系Fig.2 Relationships of polarization oflinear dielectric and electric field with time
磁介质通常可分为顺磁质、抗磁质和铁磁质3类.顺磁质和抗磁质属于各向同性的线性弱磁质.多数磁介质是顺磁质,相对磁导率在10-4~10-5之间;少数磁介质是抗磁质,相对磁导率在负的10-5~10-6之间.在弱磁质中有M=(μr-1)H,与电介质相同的分析方法可以得出相同的结论,即在变化的外场中,单值磁介质中不会出现磁化能量耗散.因此可以得出这样的结论:单值(线性)介质中不会出现极化和磁化能量损耗.
2.2 各向同性非单值介质
在非单值电介质中,当外电场变化时,由于存在阻碍电偶极矩运动的各种阻尼作用,极化强度的变化跟不上电场的变化,称为弛豫现象.描写介质性质的相对介电常数εr不仅随电场变化,而且还与极化历史有关,极化强度P与场强E之间没有简单的函数关系.在交变电场中P随E的变化稳态时如图3所示,当E沿正向增大时,P沿曲线abc随之增大,但当E减小时,P沿曲线cde减小.在E沿正向增大的过程中,E>0,dP>0,EdP>0,表示电场对电介质做功,电场能转换为介质中的极化能,电场对单位体积介质做的功等于闭合曲线abcsa包围的面积.但在E减小的过程中,E>0,dP<0,EdP<0,表示电介质对电场做功,只有数量等于闭合曲线csdc包围的面积的极化能转换为电场能.因此,在电场E从正向增大到减小的过程中,将有数量等于闭合曲线abcda包围面积的能量被电介质不可逆的消耗,这部分能量被转换为电介质的热能.电场沿反向变化,能量转化关系与正向变化相同.如果电场做周期性变化,一个变化周期内被单位体积电介质消耗的能量等于闭合曲线abcdefa包围的面积,也就是积分值∮EdP.闭合曲线abcdefa可以称为电滞曲线,该曲线包围的面积决定了单位体积电介质消耗电磁能量的多少.
如果外场为简谐电场E=E0cosωt,在非线性介质中极化强度P落后场强一个相位角φ,P=P0·cos(ωt-φ);相应电位移矢量D落后场强一个相位角δe,D=D0cos(ωt-δe).利用D=ε0E+P容易证明,如果φ是一个正数,δe也是一个正数.场强和极化强度随时间的变化如图4所示.与线性介质中的变化曲线图2相比,非线性介质中的变化曲线有两个明显的特点,一是增加了一个区域(最左侧i区),在该区域EdP>0,表示电场对电介质做功,电场能量转换为介质中的极化能;二是介质对电场做功的区域(Ⅰ和Ⅲ)被压缩,而电场对电介质做功的区域(Ⅱ和Ⅳ)被扩展,这意味着极化能转化为电场能减少,而电场能量转化为介质中的极化能增加.因此在电场的一个变化周期内,电场能转换为介质中极化能要多于极化能转换为电场能,有一部分能量被介质吸收消耗,转化为介质中的热能.
(10)
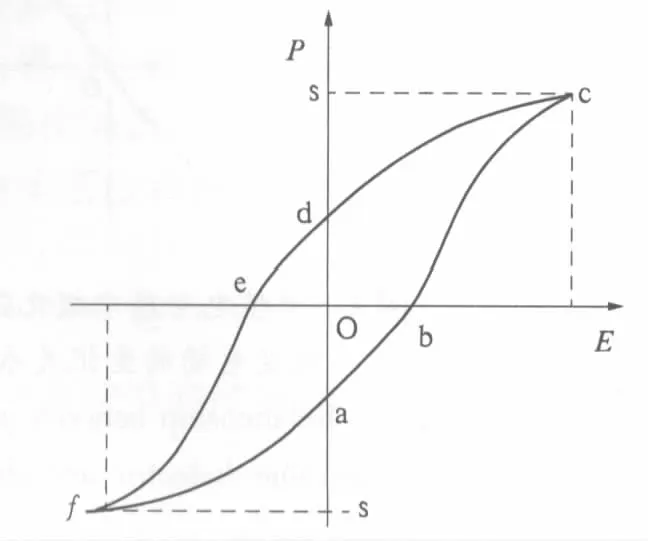
图3 非单值电介质中极化强度随交变电场的变化Fig.3 Relationship between polarization of non-single-value dielectric and electric field
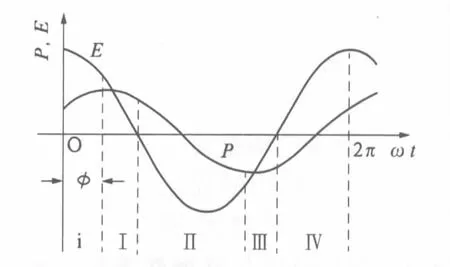
图4 非线性电介质中简谐电场和极化强度随时间的变化关系Fig.4 Relationships of polarization of nonlinear dielectric and electric field with time
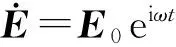
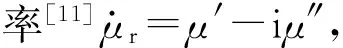
3 电磁能量损耗的瞬时值
式(3)右侧第1项表示介质空间中电场能量密度的变化率,将该项改写为
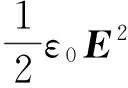
(11)
就是电介质中消耗的电场能量功率密度的瞬时值(转变为热).将式(3)右侧第2项作分解,
右侧第1项和第2项分别表示磁场能量密度和存储在介质空间中的磁化能量密度的瞬时值,而后2项
(12)
就是磁介质中消耗的磁场能量功率密度的瞬时值.式(11)和(12)清楚地表明,产生电磁能量损耗的原因是,极化强度P的变化跟不上外电场E的变化,磁化强度M的变化跟不上外磁场H的变化.导电损耗的瞬时功率密度由式(7)给出.
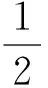
4 结论
介质中的电磁能量被分为电(磁)场能量和极(磁)化能量.利用电场对运动电荷做功导出了介质中的能量密度,极化能量密度的微分(极化功)等于电场强度与极化强度微分的乘积,磁化能量密度的微分(磁化功)等于磁场强度与磁化强度微分的乘积.在交变电磁场作用下,线性介质中的极(磁)化能与电(磁)场能量进行可逆的相互转换,没有电磁能量损耗.在非线性(非单值)介质中,由于各种阻尼作用,电(磁)偶极子的转动跟不上外场的变化,出现弛豫损耗,部分电磁能量被不可逆地转换为热能.电磁能量损耗功率密度决定于介质相对介电常数(相对磁导率)的虚部、电导率、外场频率和外场强度.电磁场能量密度变化的瞬时值可以分解为电磁场能量密度、极(磁)化能量密度和电磁损耗功率密度3部分.
参考文献:
[1] 韩光泽,陈明东. 液态物质的微波峰值吸收频率[J]. 中国科学(G辑),2008,38(7):859-866.
[2] 韩光泽,陈明东,郭平生,等. 微波辅助萃取的微波吸收系数与吸收功率密度[J]. 华南理工大学学报:自然科学版,2007,35(4):52-57.
[3] 陈明东,韩光泽,郭平生,等. 微波场作用下的溶质扩散通量[J]. 工程热物理学报,2008,29(11):1950-1952.
[4] 郭硕鸿. 电动力学[M].第3版. 北京:高等教育出版社,2008.
[5] 韩光泽. 电(磁)场作用下的平衡态热力学[J]. 华北电力大学学报,2010,37(2):104-108.
[6] 胡友秋,程福臻. 电磁学与电动力学(下册)[M]. 北京:科学出版社,2008.
[7] Mansuripur M. Electromagnetic force and torque in ponderable media[J]. Optics Express, 2008, 16(19):14821-14835.
[8] Hermann A H, James R M.电磁场与电磁能[M]. 江家麟,译. 北京:高等教育出版社,1992.
[9] Leonard M M.电磁场电磁能和电磁波[M]. 何国瑜,译. 北京:高等教育出版社,1982.
[10] 殷之文. 电介质物理学[M]. 第2版.北京:科学出版社,2003.
[11] 廖绍彬. 铁磁学(下册)[M]. 北京:科学出版社,2000.
