超导量子电路诱导规范势的条件分析

董新平， 闫润瑛， 赵正印， 杨佳俊， 武义娜, 冯志波

(许昌学院 电气信息工程学院 河南 许昌 461000)

0 引言

超导约瑟夫森纳米电路作为人工原子体系，呈现出良好的量子特性，为人们相干地调控这一量子体系并研究基本的物理规律提供了极佳的平台[1-3]．对超导约瑟夫森纳米电路施加电压和磁通偏置，可以获得各种预期的能级结构[4-5]，这为人们利用外场和超导量子体系的相互作用来诱导非阿贝尔和阿贝尔规范势提供了潜在的可能性[6]．近年来已有相关文献报道[7]，利用不同的量子化的腔模与原子相互作用分别诱导了非阿贝尔和阿贝尔规范势．最近，在同一个超导量子电路装置中，仅通过调节外部施加的磁通偏置就可以得到所需要的超导三能级结构，并通过与一维传输线谐振子的相互作用诱导非阿贝尔和阿贝尔规范势[8]．

如果按照文献[8]中提出的方案仅选取一组特定的参量进行实验检验，将会对实验条件提出较高的要求．因而建立一个更加宽泛而合理的取值范围，将会对实验操作提供有力的帮助和指导．本文对超导量子电路的三能级结构特性进行了系统的分析研究，并结合诱导非阿贝尔和阿贝尔规范势的条件，给出了更加宽泛而合理的耦合能取值范围．本文的相关结果能够对工作[8]涉及的方案进行有益的补充和完善，同时更有利于实验参数的选取，为物理上操作超导量子电路研究规范势的基本性质提供直接的理论依据．

1 超导量子电路与有效规范势

文献[8]研究的超导量子电路如图1所示．该电路包含一个具有n个库珀对的半环型超导盒子，通过两个对称的约瑟夫森结与另外一个半环型的超导环相连，从而构成一个闭合的超导环路．两个相同的约瑟夫森结的电容和耦合能均为CJ和EJ0．在闭合环路中施加磁通偏置Φe，可以调制约瑟夫森结的有效耦合能EJ．通过两个门电容C1和C2，体系分别与两个一维传输线谐振子(TLR1和TLR2)耦合[8-9]，这里的TLR1和TLR2分别具有单模频率ω1和ω2．在库珀对基矢│n〉,│n+1〉下，系统的静态哈密顿量可表示为[10-11]

(1)

其中,Ec=2e2/(C1+C2+2CJ)为系统的静电能，nd=(V1dC1+V2dC2)/2e为静态门电压V1d和V2d产生的门电荷．EJ=2EJ0cos(πΦe/Φ0)为有效的约瑟夫森结耦合能，Φ0=ћ/2e为磁通量子的基本单位．由方程(1)可知，通过调节门电压和偏置磁通量，可以分别改变超导量子电路的门电荷和耦合能，进而影响系统的能级结构．如文献[8]所述，在工作点nd=0.45，分别取EJ=1.46Ec和EJ=0.75Ec得到体系3个最低的能级│s1〉、│s2〉和│s3〉．

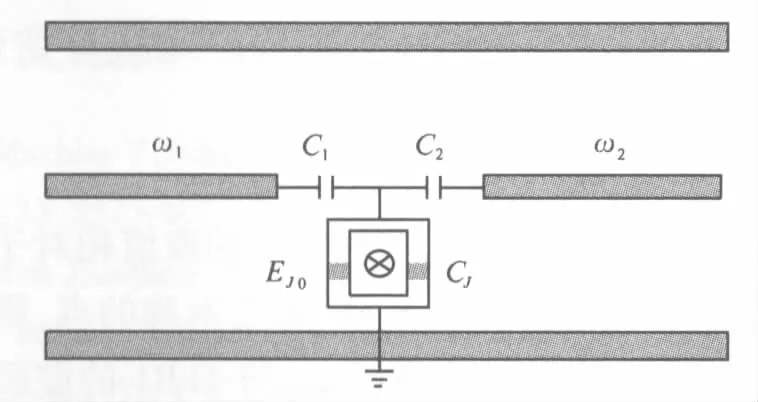
图1 超导量子电路通过C1 和C2耦合到具有单模频率ω1 和ω2的一维传输线谐振子TLR1和TLR2Fig.1 The superconducting quantum circuit coupled to TLR1 and TLR2 with respective single-mode frequencies ω1andω2 through the gate capacitors C1 and C2.

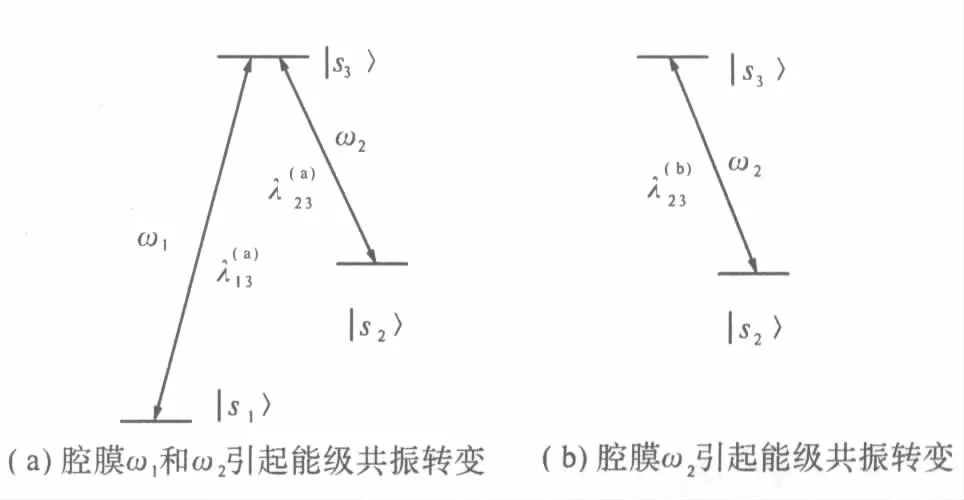
图2 能级与外场的耦合Fig.2 The couplings between energy levels and external fields

由以上方案可知，选定静态门电压工作点后，只需要调节系统的一个参数即偏置磁通量就可以改变系统的耦合能，进而改变系统的能级结构，在量子化外场的作用下即可诱导有效的非阿贝尔和阿贝尔规范势．如果期望通过实验对以上方案进行验证，本文希望对整个可能的能级结构而不是仅对一组特定的能级结构进行检验，为此需要确定系统耦合能EJ的合理取值范围，为有效地进行实验验证提供有益的指导．

2 产生可调控规范势的能级结构分析

根据以上分析，本文将对利用超导量子电路诱导有效规范势的条件进行系统分析，并为利用实验验证以上方案所需的物理参数进行细致地分析，并确定其合理的取值范围．利用超导量子电路装置诱导规范势，需要调节系统的能级结构使其与TLR的频率ω1和ω2耦合．选定工作点nd= 0.45，由方程(1)可以求出系统最低的3个能级E1、E2和E3的数值解．根据数值结果，以耦合能EJ为参数，3个能级间的转变频率ωji=(Ej-Ei)/ћ(i,j=1,2,3)与EJ的对应关系如图3所示,式中Ei和Ej为系统最低的3个能级，ωji表示系统在2个不同的能级Ei和Ej之间跃迁时相应的转变频率．转变频率ωji以及耦合能EJ均以Ec作为基本单位．由于TLR1和TLR2只有2个单模频率，本文期望利用系统的能级结构分别构建2个或1个共振模式与其耦合，从而分别诱导非阿贝尔和阿贝尔规范势．

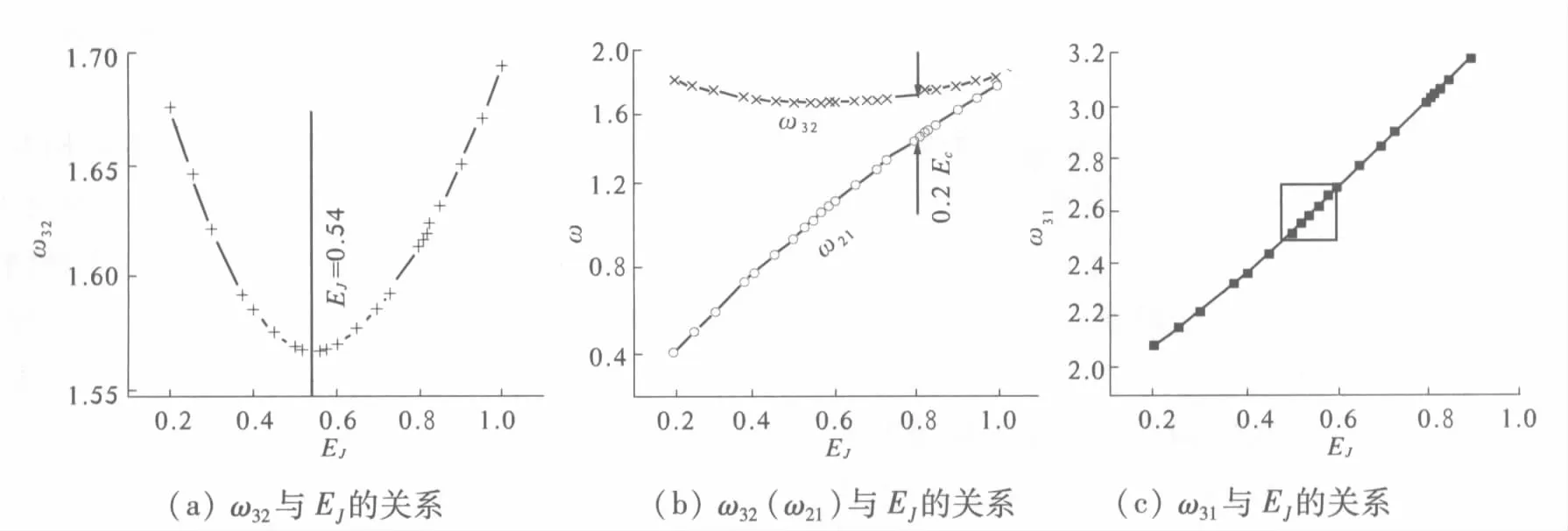
(a)ω32与EJ的关系 (b)ω32(ω21)与EJ的关系 (c)ω31与EJ的关系

图3各能级间转变频率ωji与耦合能EJ的关系
Fig.3The transition frequenciesωjias functions of coupling energyEJ．

首先，若适当地调节偏置磁通量转变频率ω32的数值，使其与TLR2的单模频率ω2匹配，如图3所示．对图3(a)中数据进行线性拟合得到的结果为

ω32=1.860 1-1.187 2EJ+1.405 7EJ2-0.383 1EJ3.

(2)

从图3(a)以及拟合结果(2)可以发现，在0.3Ec≤EJ≤1.0Ec范围内，转变频率ω32的取值相对于直线EJ= 0.54Ec对称．如果在图3(a)中0.3Ec≤EJ≤1.0Ec区间内取一对关于EJ= 0.54Ec对称的点，则相应点的转变频率ω32相等．如果在此区间内能找到这样一些对称点，使相应的转变频率ω31与TLR1的腔膜频率ω1分别相等或满足大失谐状态，同时转变频率ω21与TLR1和TLR2的腔膜频率ω1和ω2都处于较大失谐状态，那么就能根据图2相应的方案，利用一个相同的超导量子电路同时诱导2种不同的规范势．由于EJ=2Eccos(πΦe/Φ0)，显然只需调节一个参数Φe能够通过对耦合能EJ的连续调节调控系统的能级结构．因此，在工作点nd= 0.45时耦合能EJ的取值范围应限制在0.3Ec≤EJ≤1.0Ec内．

其次，从图3可以看到为使系统的转变频率ωji只与TLR1和TLR2的2个单模频率ω1和ω2匹配，要求转变频率ω21远大于TLR2的腔膜频率ω2引起的耦合强度λ12(约等于0.2Ec)．根据数值计算结果，ω21与ω31相差较多，不会引起与腔膜频率ω1的耦合．但是从图3(b)可以看出，在0.8Ec≤EJ≤1.0Ec范围内,ω21与ω32的差值小于0.2Ec，接近耦合强度λ12，这样可能出现ω21与ω32均与ω2匹配的情况．为了避免产生这种现象，要求EJ≤0.8Ec．综合对图3(a)的分析结果，得到0.3Ec≤EJ≤0.8Ec．从图2以及文献[8]的方案可以明确看出,此条件限制对于产生等效非阿贝尔和阿贝尔规范势都是必要的．

最后，为了产生非阿贝尔规范势，要求ω31能够与TLR1的腔膜频率ω1匹配．在图3(c)中，区间0.3Ec≤EJ≤0.8Ec内ω31均能够与TLR1的腔膜频率ω1匹配，因此在此范围内所有EJ的取值都可以诱导非阿贝尔规范势．为了能通过改变耦合能EJ同时达到诱导阿贝尔规范势的目的，希望转变频率ω31与TLR1的腔膜频率ω1的失谐程度远大于单模频率之间的耦合强度0.2Ec．但是根据图3(c)的数值结果以及线性拟合结果(2)，可以发现当0.48Ec≤EJ≤0.6Ec时，关于EJ= 0.54Ec对称的一些点的取值虽然与ω32相同，但是相应的ω31之间的差值却小于0.2Ec．这有可能会导致这些对称点之间的转变频率ω31都与TLR1之间的腔膜频率ω1发生耦合，从而不能诱导非阿贝尔规范势．因此，若要求通过改变耦合能EJ同时可靠地诱导2种不同的规范势，EJ不能取0.48Ec≤EJ≤0.6Ec之间的数值．

综上所述，取工作点nd= 0.45时，若0.48Ec≤EJ≤0.6Ec只能诱导等效阿贝尔规范势；而在0.3Ec≤EJ≤0.48Ec和0.6Ec≤EJ≤0.8Ec两个区间内，可以找到关于EJ= 0.54Ec对称的一个取值点.当EJ分别取这些对应的取值时，分别能够诱导阿贝尔和非阿贝尔规范势．根据EJ=2Eccos(πΦe/Φ0)，可以分别诱导阿贝尔和非阿贝尔规范势的合理的偏置磁通量的取值范围为

0.15≤cos(πΦe1/Φ0)≤0.24;0.3≤cos(πΦe2/Φ0)≤0.4.

(3)

由以上分析，在上述区间内能够诱导不同规范势的EJ的取值关于EJ= 0.54Ec对称，

cos(πΦe1/Φ0)+cos(πΦe2/Φ0)=0.54.

(4)

由式(4)，对于固定的TLR1和TIR2的腔膜频率ω1和ω2，若在满足条件(3)的一个区间内取定了一个偏置磁通量Φe1能够诱导非阿贝尔规范势，则在另一个区间内相应的偏置磁通量为Φe2=Φ0cos-1[0.54-cos(πΦe1/Φ0)]/π时可以诱导阿贝尔规范势．

3 结论

根据超导量子电路的能级结构的数值解以及外场诱导有效规范势的条件，针对外场作用下的一个超导量子体系，本文通过改变体系的约瑟夫森耦合能进而改变体系的能级结构，来调控地产生非阿贝尔和阿贝尔规范势.研究表明，在静态门电压工作点nd= 0.45处，对于固定的腔膜频率ω1和ω2而言，当EJ满足取值范围0.48Ec≤EJ≤0.6Ec时，由此决定的能级结构使得腔模只能诱导阿贝尔规范势，而不能诱导非阿贝尔规范势；若EJ的取值在0.3Ec≤EJ≤0.48Ec和0.6Ec≤EJ≤0.8Ec两个区间内，可以通过改变超导量子电路装置的偏置磁通量分别诱导非阿贝尔和阿贝尔规范势.研究结果对诱导规范势的条件给出了更为完整的分析，相关结论为将来通过实验利用同一个超导量子电路装置诱导规范势提供了有益的帮助和指导．

参考文献：

[2] You Jianqiang，Nori F. Superconducting circuits and quantum circuits[J]. Phys Today，2005，58(11)：42-47．

[3] Clarke J，Wilhelm F K. Superconducting quantum bits[J]. Nature，2008，453(7198)：1031-1042.

[4] Koch J，Yu T M，Gambetta J，et al．Charge-insensitive qubit design derived from the Cooper pair box[J]. Phys Rev A，2007，76(4)：042319．

[5] Feng Zhibo，Zhang Xinding． Holonomic quantum computation with superconducting charge-phase qubits in a cavity[J]. Phys Lett A，2008，372(10)：1589-1594．

[6] Faoro L，Siewert J，Fazio R. Non-Abelian holonomies, charge pumping, and quantum computation with Josephson junctions[J]. Phys Rev Lett，2003，90(2)：028301．

[7] Larson J，Levin S. Effective Abelian and non-Abelian gauge potentials in cavity QED[J]. Phys Rev Lett，2009，103(1)：013602．

[8] Feng Zhibo，Wang A M，Yan R Y. Effective gauge potentials induced by superconducting quantum circuits[J]. Phys Lett A，2011，375(4)：808-811．

[9] Liao Jieqiao，Huang Jinfeng，Liu Yuxi，et al．Quantum switch for single-photon transport in a coupled superconducting transmission line resonator array[J]. Phys Rev A，2009，80(1)：014301．

[10] Siewert J，Brades T，Falci G.Adiabatic passage with superconducting nanocircuits[J]. Opt Commun，2006，264(2)：435-440．

[11] Feng Zhibo. Coupling charge qubits via Raman transitions in circuit QED[J]. Phys Rev A，2008，78(3)：032325．