物理教育专业《高等数学》课程内容体系研究
2012-05-18穆洪华淄博师范高等专科学校数理科学系山东淄博255130
穆洪华(淄博师范高等专科学校 数理科学系,山东 淄博 255130)
一、引言
国家教育部高教司在“面向 21世纪教学内容和课程体系改革”的计划中特别指出,要重点解决大学数学课程体系和内容更新的问题。近年来,关于高等数学应用能力培养及课程内容体系的研究越来越多。鉴于已有的研究成果和我校的物理教育专业的培养计划,为使得《高等数学》更好地服务于我校物理教育专业的教育教学,我们针对物理教育专业所开设的《高等数学》进行了课程内容与体系的教育教学改革研究。
目前,我校物理教育专业开设的《高等数学》[1],涵盖的内容比较全面,但是所涵盖的内容以及内容的深度在一定程度上不适合物理教育专业的教学。为此,本课题以物理教育专业课程的实际需要为出发点,围绕培养、培训一批基础知识扎实、基本素质过硬的初中、小学物理教师这一目标,基于现在所采用的《高等数学》,增加《高等代数》[2]《概率论与数理统计》[3]《常微分方程》[4]等与解决物理问题相关的专业知识点,切实服务于物理教育专业的教育教学。
二、相关研究存在的主要问题
对于大学数学课程体系和内容的研究,在课程设置、教材选编与应用能力的培养等方面都取得了一定的研究成果,但是偏重理论探讨的居多,侧重实践应用的较少,尤其是知识的选编不够专业化。具体来讲,相关研究的问题主要集中在以下两个方面:
第一 ,关于教材选编问题的研究不够专业化。教材中关于应用的内容,尤其是与学生专业紧密相关的课程内容设置涉及甚少;特别就我校学生来说,如何将大学内容和中小学相关内容进行衔接对比,如何体现出能够进一步提高我校物理教育专业学生将来的教育教学水平,也是教材内容所欠缺的一个主要部分。
第二,研究深度不够。各地区所采用的教材版本不统一,高校的图书馆又不可能完全拥有各个版本的整套教材,从而使得研究无可避免的存在缺憾,具有一定的局限性。另外,从 CNKI来看,针对高等数学应用能力培养的理论研究比较少,尤其是在针对专业内容设置方面,成果不多。
根据我校生源的具体情况与我校物理教育专业所采用的《高等数学》,本课题侧重于第一个问题的研究。希望通过这次的探讨,能够找到一个更加适应我校物理教育这一专业特色的《高等数学》教学内容体系。
三、研究方法
为使研究具有更强的实效性和针对性,我们的研究透视建国以来尤其是20世纪以来我国高等数学的发展趋向,着眼于最近十年关于高等数学教育科研成果,立足于对目前我校数学教育的课程内容体系进行研究探析。为此,该课题采用以下四种方法进行研究:
文献资料法:一方面,多阅读一些关于高数教育教学的时政要闻,多订阅一些关于教育的期刊,如《中国教育学刊》《数学教育学报》《创新教育》等,以便了解目前高数教育所存在的问题、成果和最新动向。
文案调研法:通过网络平台和学校的图书馆电子资源,定期研读一些文章,不断更新、巩固和加深自己对高数教育教学的认知。
深度访谈法:深入到课堂,多与学生沟通交流;深入到教研室,多与相关领导和数学任课教师交流,探讨切实适合我校物理教育专业需求的高师类小教高数的教学课程内容体系。
推断统计法:对物理班的高数和相关专业课成绩进行数据分析,运用统计分析软件进行推断统计,从而对改革后的高数课程内容体系进行定量的描述。
四、研究成果
(一)高数的课程内容体系
鉴于以上两个问题,根据该课题的研究方法,课题小组研究了目前我校物理教育专业所采用的教材,依据《高等数学》原有的课程内容体系和研究的需要,将课程内容加入简单的线性代数学、几何学、概率论与数理统计基础知识,新的课程内容体系主要由以下四个板块构成:
1.微积分学[5]:级数、极限、导数、积分;
2.向量代数:向量、矩阵;
3.常微分方程:微分方程,简单高、低次微分方程的求解方法;
4.概率统计初步知识:概率的思想、常用的简单的统计方法。
通过对《高等数学》内容体系的改革,使得新的内容体系能够基本满足我校物理教育专业的需求,具有一定的专业特色。例如,在导数相关问题的处理上,我们始终围绕着与物理相关的问题展开内容编排,以达到让学生在解决相关的物理问题中体会和理解导数的定义、性质与求解的基本思想和方法。
在关于导数概念这一个问题的引入上,我们以学生非常熟悉的直线运动逐步引入,如下图所示:

在匀速直线运动中:
在变速直线运动中,我们只看一段很小的时间间隔从t0→t,则这一段时间可以看作匀速直线运动,这段时间的位移是:
f(t)-f(t0)
从而这段时间的平均速度为:
接着引入极限的思想,设想t无限的靠近t0,我们就会有以下求极限的表达:
如果这个极限存在,我们记为v,即:
这个极限值v我们称为动点在时刻t0的瞬时速度。关于这个极限,表达式比较麻烦,且这种变化可以继续改写成以下形式:
令:△S=f(t0+△t)-f(t0),则:
由于字母符号具有一般的意义,我们可以引入一个更具一般意义的字母符号,令: △S=△y,△t=△x,v=y′,则:
则A式就是这里要介绍的一个新的数学概念——导数,然后逐步展开讲解,并且学完导数的定义后,再将导数回扣到物理的相关应用上。这样不仅使得物理教育专业的学生能够理解导数的基本概念,也能够使得物理教育专业的学生很好地理解导数的应用,从而达到我们课题研究的目的。
由于物理教育专业所用的数学知识以微积分为重点,所以对于极限这部分内容的设置,要求学生了解极限的含义,掌握求极限常用的几种方法为主要目标,弱化对于极限相关基本理论的推导求证;对于导数和微积分这部分内容的设置,要加强力度,不仅要讲清楚基本的知识理论,还要让学生弄清楚概念的出处和意义,帮助学生掌握求解技巧及应用方法;对于其它部分的教学内容体系,贯穿如下原则:围绕物理教育专业的特点,讲清楚基础知识,让学生做到明其理,知其用。
总之,该课题研究的重点是探讨《高等数学》的课程内容体系,使之更具有物理教育的专业特色,从而能够更好地服务于物理教育专业内其他专业课程的教学。
(二)高数对物理教育专业后续课程影响的实证研究
根据课程内容体系的重新设置,该课题对改革后的教材内容体系所取得的一些成效进行了数据分析,用数据给出一个比较直观的显示。数据主要来源于物理教育专业所开设的《高等数学》与其后续课程《大学物理》[6]《光学》[7]《力学》[8]与《电磁学》[9]的期末考试成绩,通过EXCEL的统计分析工具对这些数据进行方差因素分析[10](在对课程成绩这一方差分析中,每个学生的应试能力可以看作可控因素,而每次考试能力的发挥的程度可以看作不可控因素。据此,我们可以对物理教育专业开设的《高等数学》对其后续专业课是否存在影响进行研究),具体结论如下:
1.高数与大学物理
H0:《高等数学》与《大学物理》成绩等专业课成绩没有影响。
H1:《高等数学》与《大学物理》成绩等专业课成绩存在一定影响。
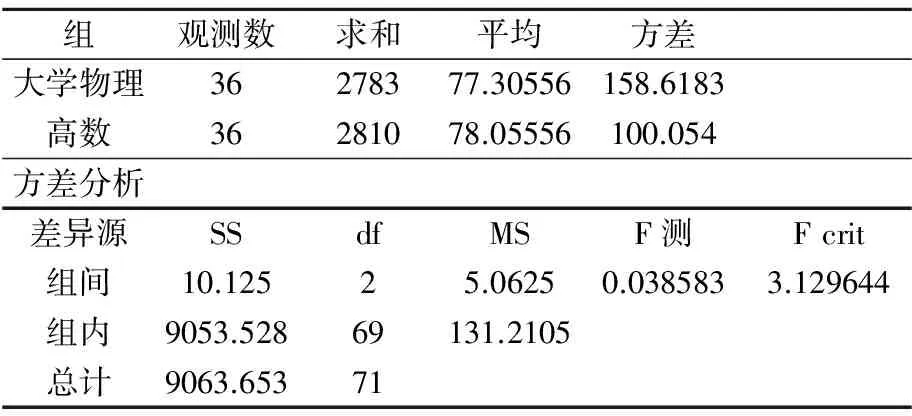
表一 物理班高数成绩与大学物理的单因素方差分析
通过该表我们不难得出,《高等数学》与《大学物理》的成绩存在显著差异。事实上,大量的教学经验和对部分学生以及任课教师的访谈调查也得出现同样的结论。在访谈中,我们还发现大学物理成绩偏低的一个主要原因:《高等数学》与《大学物理》在大一上学期同时开课,高数内容的学习滞后于大学物理的学习,这无疑给教师的教和学生的学带来了一定的困难。鉴于以上原因,我们建议学校相关部门在开课安排上,将《大学物理》晚于《高等数学》半个学期开课。
《高等数学》这一专业基础课程基础的好坏,直接影响到物理教育专业后续课程《大学物理》的教育教学。在课程的发展史上,《高等数学》中的很多内容毕竟是在解决物理问题的过程中应运而生的。因此,任课教师和学生一定要认识到高数与物理的渊源和高数对物理专业后续课程学习的重要作用。
2.高数与力学
H0:《高等数学》与《力学》成绩等专业课成绩没有影响;
H1:《高数》与《力学》成绩等专业课成绩有一定影响。
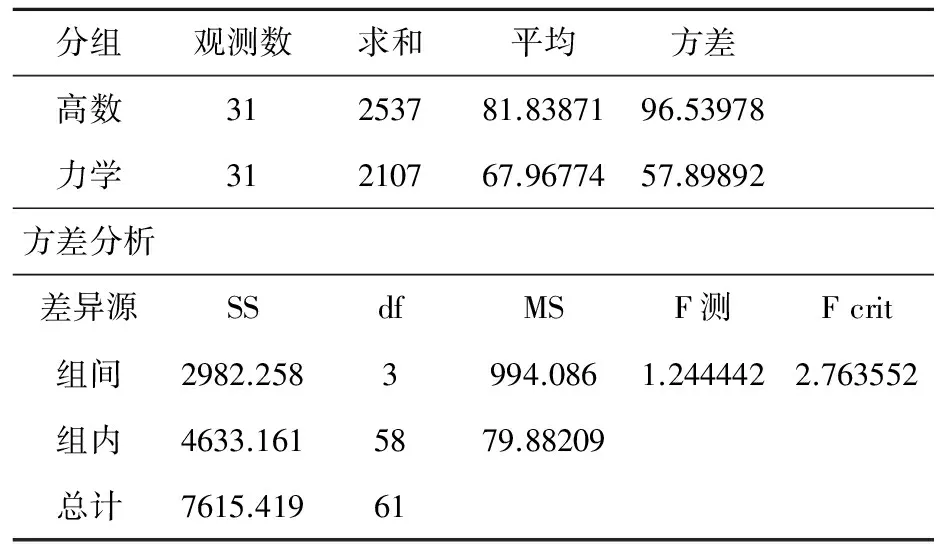
表二 物理班高数成绩与力学的单因素方差分析
通过表二,可以得出这样的结论:高数成绩对力学成绩具有一定的影响。力学的学习对于导数和微机分的要求比较高,运用的也比较多,任课老师只有将抽象的高数知识点与该部分知识在物理上的应用进行巧妙的结合,才能收到良好的教学效果。
3.高数与热学、电磁学
用同样的方法,对物理教育专业的后续课程《热学》和《电磁学》进行数据分析,得出以下结论:高数对热学和电磁学都有存在不同程度的影响,尤其对电磁学的影响最大。为此,我们还对影响比较大的电磁学做了线性回归分析[11],其结果如下:
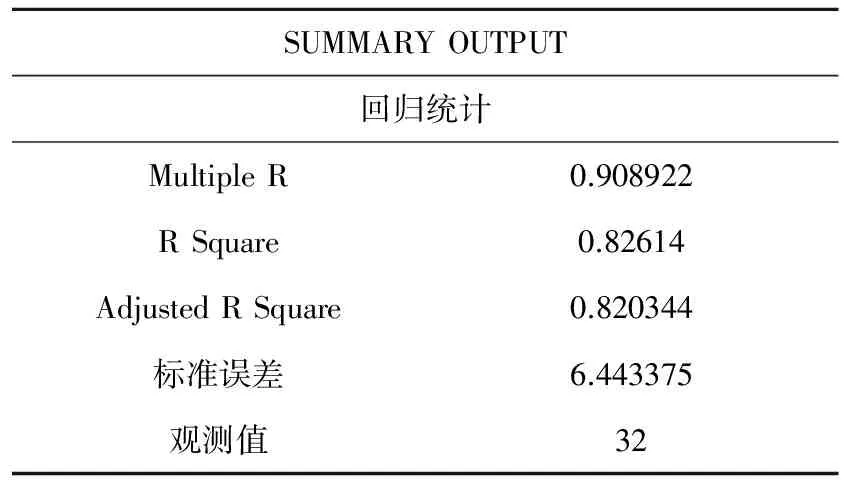
表三
其中,高数成绩为因变量x,电磁学成绩为自变量y,该结果显示《高等数学》和《电磁学》的线性回归方程为:
y=0.79x+4.98
高数与电磁学有很强的相关性,高数成绩的好坏,直接关系到电磁学的学习。
通过以上数据分析,我们得出:高数对物理教育专业其他后续课程的学习具有很重要的作用。为更好地发挥好高数在物理教育专业课中的作用,一方面,相关的任课教师要以提高教育教学质量为目标,做好教育科研工作;另一方面,相关的任课教师要充分调动物理教育专业的学生学习高数的积极性和迫切性,理解高等数学在物理教育中的重要作用,帮助物理教育专业学生打好坚实的专业基础。
五、问题与讨论
21世纪,对中国师范教育而言,面临着大发展、大转折、大提高的改革前景和发展趋势,我们需要实践探索、勇于创新。作为一线老师,我们应该理解教育所面临的问题,在当代教育改革实践中,教师的工作职能出现了深刻的变化,这种变化极大地提高了教师劳动的复杂程度和创造性质。教师不是单纯的任务执行者,而是教育的思想者、研究者、实践者和创新者[12]。
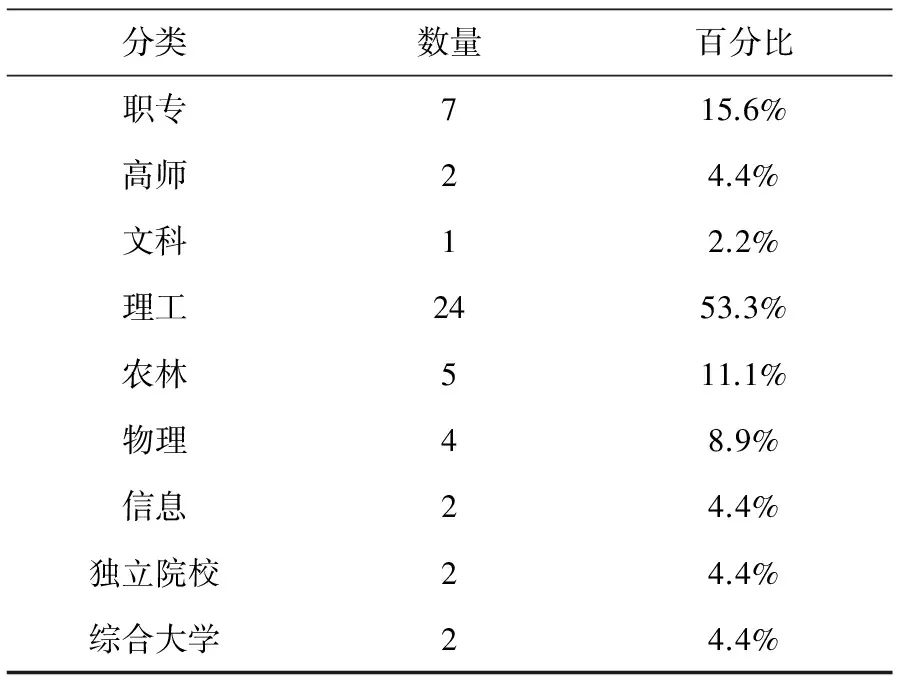
为了研究当前市场上销售的《高等数学》教材的内容性质,我们重点对当当网上现在销售的《高等数学》按照出版时间和购买数量排序进行了分层抽样,一共选取了45门课程,部分调查结果如下:
表五
根据调查的资料及数据,我们得出以下结论:
第一,目前《高等数学》主要为一些高等院校的理工类学生设计的,这一类教材占调查总数的53.3%。由此可以推断现行的《高等数学》教材内容的性质适合理工类的居多,最为畅销的版本是由同济大学数学系编、高等教育出版社出版的《高等数学》。
第二,物理类的《高等数学》教材很少,仅占调查总数的8.9%,为师范类设计的物理类的《高数》几乎没有。
第三,为高师类设计的《高等数学》仅占调查总数的4.4%,其中说明为师范类小教专业设计的《高等数学》教材,由刘效丽主编、首都师范大学出版社出版,仅占调查总数的2.2%。
第四,为独立院校和高职高专设计的教材,虽然占总数的比重较小,但是从出版时间上看,这类教材都比较年轻,且大都有这些院校的教研组编制,具有他们本校的教育特色。仅2011年和2012年出版的这一类独特的《高等数学》教材占总出版的80%以上。由此可见,近年来,在大学数学课程体系和内容更新的问题上,我们取得了可喜的成果。
鉴于以上调查结论,为了建设富有物理教育专业特色的《高等数学》,为了教育事业更好的发展,为了适应社会发展的需求,以下两个问题有待于我们进一步讨论解决:
第一,选编一套适合高师类富有物理教育专业特色的《高等数学》,是我们作为教育者必须直面的一个课题。对于本课题的研究,如何将原有的《高等数学》的内容体系进一步的简化、规整而又不失其系统性,如何将其整理成适合我校物理教育专业特色的教材,是该课题研究值得进一步探讨的问题。
第二,如何更好地把《高等数学》的基本理论知识,尤其是思想方法、技能技巧传授给学生,由简入深,由点到面,让学生系统地理解知识,把所学的知识融会贯通、运用自如,更是本课题有待于进一步研究的问题。
由于高职教育的发展,适合职专教育的《高等数学》已得到了一定的发展。但是针对高等数学应用能力培养的理论研究比较少,针对专业内容设置富有师范类教育特色的研究成果更少。按照Freudenthal的观点[13],教学的最佳途径是让学生把理论和实际联系起来。师范院校对未来教育者基础文化的形成、所教学科专业文化的掌握、教育理论的理解、教育理论前沿的把握等基本素养的培养等都具有非常重要的作用。所以,面向学校教育的问题与前景,师范院校的教师和学生必须与中小学教师和学生紧密联系,一起探索,共同努力,不断创造出充满生机的、新的富有专业特色的课程内容体系。
参考文献:
[1]《高等数学》编写组.高等数学(上,下)(第6版)[M].北京:高等教育出版社,2009.
[2]丘维声.高等代数(上,下) [M].北京:高等教育出版社,2002.
[3]于义良,王玉津.概率论与数理统计基础教程[M]. 北京:中国人民大学出版社,2004.
[4]丁同仁,李承治.常微分方程教程[M].北京:高等教育出版社,2006.
[5]刘玉莲,傅沛仁.数学分析讲义(上,下)(第4版) [M].北京:高等教育出版社,2003.
[6]向义和.大学物理导论[M].北京:清华大学出版社,1999.
[7]姚启钧. 光学教程(第4版)[M].北京:高等教育出版社,2008.
[8]漆安慎,杜婵英.力学(第2版)[M].北京:高等教育出版社,2005.
[9]张玉民,戚伯云.电磁学(第2版)[M].北京:科学出版社,2007.
[10]李朋.Excel统计分析实例精讲(第1版)[M].北京:科学出版社,2006.
[11]张梅琳.应用统计学(第2版)[M].上海:复旦大学出版社,2008.
[12]张美君..在教师专业化发展中提升教师职业生命的价值[J].时代教育,2012,(9).
[13]李俊.中小学概率的教与学[M].上海:华东师范大学出版社,2003.
