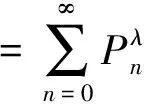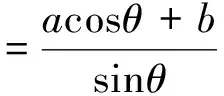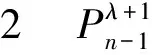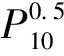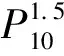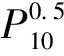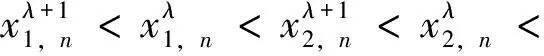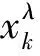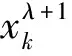关于Pollaczek多项式零点的两点性质*
2012-05-10王红勇周建荣
王红勇,周建荣
(1.南华大学数理学院,湖南 衡阳 421001;2.佛山科学技术学院理学院数学系,广东 佛山 528000)
多项式pn(x)与pn-1(x)的零点交叉是指: 若x1 x1 Pollaczek多项式是Pollaczek本人在考察法国电话系统的一个随机模型时首次提出来的,它本质上与排队论有关。 近年来,对于Pollaczek多项式及其零点渐近性质的研究引起了国内外许多专家学者的极大兴趣[1-2],但是当参数λ,a,b变动时,关于其零点的交叉性和单调性的结果却不多。而多项式的零点交叉性质在诸如 approximation of finite Hilbert Transform[3], approximation of zeros by fixed point iteration techniques[4],existence of positive numerical quadrature formulae[5]等各种物理、工程问题和理论中都有广泛的应用。 (x;a,b)=2[(n+a+λ)x+b]· (1) 其初始条件为 (x;a,b)=1,(x;a,b)=2(λ+a)x+b 当λ>0,a>|b|时,Pollaczek 多项式满足如下的正交关系式 ;a,(x;a,b)wλ(x;a,b)dx= 其中 w(x;a,b,λ)=(1-x2)λ-1/2exp[(2θ-π)Φ(θ)]· F(x,t)=(1-teiθ)-λ+iΦ(θ)(1-te-iθ)-λ-iΦ(θ) (2) 其中 对式(2)做变换λ→λ+1,化简得 (x;a,b)tn= (1-teiθ)-(λ+1)+iΦ(θ)(1-te-iθ)-(λ+1)-iΦ(θ)= (3) (1-teiθ)(1-te-iθ)=1-t(eiθ+e-iθ)+t2 并匹配tn(n=0,1,2,…)前的系数,则有 ;a,;a,(x;a,b)= (4) 在式(1)中用n-1替换n,λ+1替换λ,并化简可得 ;a,(x;a,b)+ (5) 结合式(4)和式(5)得 (6) 注1 据我们所知式(4)和式(6)是新的结果。 本文的结果需要用到下面的结论([7],Theorem 3)。 引理1 设Rn(x)=Pn(x)+anPn-1(x),n=1,2,…,an为非零实数,{Pn(x)}为一族正交多项式,其权函数为w(x)>0,x∈[c,d],其最高次系数大于零,记c (i)an<0⟺x1,n (ii)an>0⟺y1 为了让引理1的结论也适用于本文所考虑的情形,我们对其做如下的一个推广。 (i)cnan(x)<0,x∈(c,d)⟹ x1,n (7) (ii)cnan(x)>0,x∈(c,d)⟹x1,n y1 (8) x1,n xn-1,n (9) 因此pn-1(xi,n)pn(xi,n-1)<0,i=1,2,…,n-1。 所以 Rn(xi,n)Rn(xi,n-1)= cnan(xi,n)Pn-1(xi,n)Pn(xi,n-1)<0 由零点定理可知,在(xi,n,xi,n-1)内至少有Rn(x)的一个实零点。 结合式(9),知Rn(x)至少有n-1个零点y1 所以结论成立。 证毕。 {-0.734 9;-0.593 3;-0.451 7;-0.313 2;-0.147 6;0.033 8;0.206 2;0.370 0;0.532 6;0.688 3}。 {-0.749 6;-0.615 3;-0.473 6;-0.317 8;-0.135 7;0.058 7;0.242 4;0.407 0;0.561 4;0.707 2}。 定理3 如果参数λ,a,b满足λ>0,a>|b|,及以下两个条件当中之一: (i)当λ>a时,λ+b-a<0或a+b-λ>0; (ii)当λ 证明如果用定理1条件中的记号,那么这里 由定理1知,若(I)或(II)成立,则 (10) 总而言之,我们有 …< 用类似的方法可证,当λ>a,a+b-λ>0,或λ …< (11) 定理4 若参数λ,a,b满足λ>0,a>|b|,且 证明经典Pollaczek 正交多项式的权函数为 w(x;a,b,λ)=(1-x2)λ-1/2 x=cosθ∈(-1,1)。 关于x∈(-1,1)是单调递减函数,再由Markoff 在文[8,p116,Theorem 6.12.2]中的结论知, ≤,k=1,2,…,n ≤,k=1,2,…,n 证毕。 参考文献: [1]BO R,WONG R.Asymptotic behavior of the Pollaczek polynomials and their zeros [J].Stud Appl Math,1996,96: 307-338. [2]ZHOU J R,ZHAO Y Q.An infinite asymptotic expansion for the extreme zeros of the Pollaczek polynomials [J].Stud Appl Math,2007,118(2): 255-279. [3]MASTROIANNI G,OCCORSIO D.Interlacing properties of the zeros of the orthogonal polynomials and approximation of the Hilbert transform [J].Computers and Mathematics with Applications,1995,30 (3) : 155-168. [4]SEGURA J.The zeros of special functions from a fixed point method [J].SIAM Journal of Numerical Analysis,2002,40(1): 114-133. [5]PEHERSTORFER F.Linear combination of orthogonal polynomials generating positive quadrature formulas [J].Mathematics of Computation,1990,55 (191): 231-241. [6]WANG H Y,ZHAO Y Q.Uniform asymptotics and zeros of a system of orthogonal polynomials defined via a difference equation [J].Journal of Mathematical Analysis and Applications,2010,369 (2): 453-472. [7]BREZINSKI C,DRIVER K A,REDIVO-ZAGLIAC M.Quasi-orthogonality with applications to some families of classical orthogonal polynomials[J].Applied Numerical Mathematics,2004,48(2): 157-168. [8]SZEG G.Orthogonal polynomials[M].New York:American Mathematical Society,1959.
1 Pollaczek 多项式
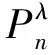

2 主要结果及其证明