基于总体耦合矩阵法的滚动联轴器动态特性研究*

徐海良，林良程，曾义聪，陈 奇

(中南大学机电工程学院∥高性能复杂制造国家重点试验室，湖南 长沙 410083)

随着生产和科学技术的发展，旋转机械向高速、重载、轻型化和自动化发展，转子与定子之间的间隙日趋减小，系统对联轴器的性能要求也越来越高[1-3]。滚动联轴器是在国家科技攻关项目研究中发明的一种专利产品[4-5]，具有传递转矩能力强，维修方便，使用寿命长的优点，对设备之间的连接轴在环境恶劣和温度变化大的条件下工作而发生的小量轴向位移、径向位移和角偏差具有较强的补偿能力，其性能超过齿轮联轴器，是代替齿轮联轴器的一种理想产品[6-9]。

滚动联轴器由左半联轴器1、右半联轴器2、滚动体3、 滚道4和防尘盖5组成，如图1所示。其工作原理：左联轴器通过挤压滚动体把转矩的传递给右半联轴器实现传动；当左、右半联轴器存在轴向位移、径向位移和角度偏差时，滚动体会在滚道内滚动以实现不对中补偿，从而有效防止轴系不对中而产生附加载荷及振动；同时传动中由于滚动体只受挤压力，具有较大的承载能力。可广泛应用于冶金机械、矿山机械、石油机械、起重运输机械、工程机械、化工机械、建材机械、船舶、水泵、风机等行业。因此，对该种联轴器的动态特性进行理论研究，具有十分重要的意义。

1.左半联轴器;2.右半联轴器;3.滚动体;4.滚道;5.防尘盖

2 滚动联轴器啮合数学模型

滚动联轴器通过挤压滚动体实现力矩的传递，因此滚动体的受力状态直接影响联轴器的传动性能，对滚动体进行受力分析，得到其受力模型如图2。

图2 滚动体受力分析

联轴器在传动过程中，只有两个滚动体受到挤压起到传递转矩的作用，由受力分析图2可知：

滚动体所受压力

(1)

式中：T为转矩，N·m；RD为滚动体啮合所处半径，mm；φ为因径向不对中引起的啮合角度差，φ≈tanφ=ex/(2(RO-RC))；ex为径向不对中量，mm；RC为滚动体的半径，mm；RO为滚道的半径，mm。

根据Hz接触理论，得到滚动体受压的最大应变量[10-11]:

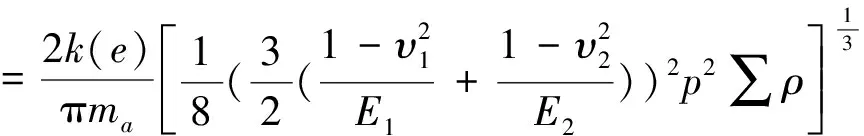
(2)

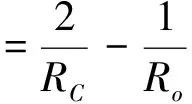
k(e)为第一类椭圆积分 ；ma为接触椭圆偏心系数；E1为滚动体材料的弹性模量；E2为滚道材料的弹性模量；υ1为滚动体材料的泊松比；υ2为滚道材料的泊松比；Ro为滚道的半径，mm。

由(1)(2)求得，联轴器的等效啮合刚度：

·

(3)

2.1 径向刚度系数

设在Y方向上给一小位移Δy，则在滚动体挤压力Y方向上的弹性位移为dy=Δy|cos(θ+φ)|,滚动体产生的弹性力Fs=KTdy。见图3。

图3 径向力分析

由此得联轴器的Y向等效刚度kyy和Y向位移引起的交叉等效刚度kxy分别为：

(θ+φ)

(4)

式中：θi为第i个滚动体滚道所在位置与x轴的夹角

(θ+φ)sin(θ+φ)

(5)

同理，设在X方向上给一小位移Δx，得dx=Δx|sin(θ-φ)|，产生的弹性力Fs1=KTdx，则

(θ-φ)

(6)

(7)

联轴器在转动过程中θ是个时变量，令θ=ωt,并将(3)代入(4)(5)(6)(7)得

(8)

2.2 角向刚度

滚动联轴器在发生角偏差时，滚动体在滚道中滚动，产生的滚动摩擦阻力矩Mθ很小可忽略不计，因此:

kθxx=kθyy=kθxy=kθyx= 0

(9)

2.3 径向阻尼

滚动联轴器的阻尼主要产生于半联轴器与滚动体的滚动摩擦。转子动力学中，摩擦产生的阻尼通常采用等效粘性阻尼来计算，即旋转一周摩擦力耗损的能量等于粘性阻尼一周耗损的能量[12-13]。

当联轴器发生径向位移时，滚动体在滚道上的滚动实现补偿，其滚动摩擦阻力[14]：

(10)

式中：μk为滚动摩擦系数，μk=0.01；d为滚动体的直径，mm；RD为滚动体啮合处所在的半径，mm

假设两半联轴器在x轴方向存在初始振幅e0，由图4可知，任意位置的偏移量可近似的表达为ex=e0cosωt， 则滚动体在滚道上滚动的相对运动速度:

ωe0sin(ωt)

(11)

图4 径向不对中运动轨迹

因此，一个滚动体在联轴器运转一周所耗损的能量

(ωt)=

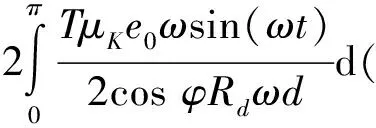
(12)

所以可求得阻尼

(13)

2.4 转角阻尼系数

由参考文献[14]，滚动体旋转一圈所耗损的能量：

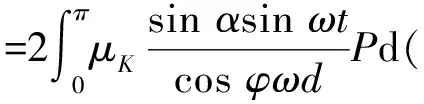
(14)

式中：P为传递功率，P=Tω;α为角振幅

则转角阻尼为

(15)

3 滚动联轴器-转子耦合系统振动方程

根据整体耦合矩阵法[15]，将联轴器的耦合作用力转化为通过刚度和阻尼来实现，其在xoz平面内的受力分析如图5所示，径向作用通过径向耦合刚度径向刚度kxx、径向交叉刚度kxy、径向阻尼dr实现; 角向作用通过角向刚度kθxx、角向交叉刚度kθxy、角向阻尼dθ实现。Fxc,Fxd分别表示联轴器作用在c，d节点x向上的力;Nyc,Nyd表示联轴器作用在c,d节点y向上的力矩。

图5 联轴器在xoz平面内的耦合力分析

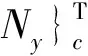
(16)

(17)

式中:Kcou和Ccou是滚动联轴器的刚度耦合矩阵和阻尼耦合矩阵

，

对于联轴器耦合的双转子系统，两转子之间联轴器的耦合力是内力,但对单个转子来说是外力。假设联轴器两边的节点编号c和d分别在1转子上和2转子上。根据集总参数模型，可获得1转子和2转子的双转子振动方程[15-17]。

′U=Fe-Fp

(18)

将(16)和(17)代入(18)得

(19)

其中：

，

将(18)代入(17)得耦合系统总振动响应微分方程：

′′+Kcc)U=Fe

(20)

求解式(19)可得系统的不平衡响应。

4 数值计算与结果分析

取某厂一小型涡轮燃气机进行计算，该小型涡轮燃气机转子系统的等效计算模型如图6所示。其结构参数和支撑轴承动力特性系数分别如表1、表2所示[15]。 滚动联轴器选用GDQ3型，滚动体直径d=10 mm，滚动体啮合所处的半径RD=70 mm,设计径向振幅e0=0.1 mm,角振幅α=0.5,其他具体参数如表3所示。

图6 滚动联轴器耦合双转子系统计算模型

表1 滚动联轴器耦合双转子系统结构参数1)

表2 支撑轴承动力学系数

由所求得的滚动联轴器的刚度系数和阻尼系数的表达式(8)、(9)、(13)、(15)可知，它们是关于系统转矩T的函数。因此，在3节点处施加一不平衡量5.1×10-5kg·m,转速ω=1 000 rad/s，取传递转矩T分别为1 N·m、100 N·m、1 000 N·m、1 800 N·m,联轴器c,d节点的轴心轨迹曲线和不平衡响应分别进行计算，计算结果如图7-8所示。

表3 联轴器参数

图7为左、右半联轴器在不同转矩下的轴心轨迹图，由图可知，滚动联轴器在ω=1 000 rad/s高速场合传递低转矩时，由于联轴器的刚度和阻尼很小，联轴器耦合力很弱，联轴器刚度和阻尼的非线性引发不平衡扰动力使系统稳定性降低，轴心轨迹混乱，而随着传递转矩的增大，联轴器的刚度和阻尼增大，联轴器耦合力增强，增加了系统的约束，联轴器传动趋于稳定。

由图8(a)可知，在当力矩从1 N·m增大到100 N·m时，左半滚动联轴器节点5的振动幅值随转矩增大而急剧降低，节点幅值由7.5×10-6m降到2.3×10-6m，这有利于联轴器从最初的不稳定传动状态快速调整到相对稳定的传动状态；继续增大转矩，振幅变化不明显，最后趋于稳定，说明其能较好的适应非稳定转矩的重载系统。

通过对比分析图8(a)和图8(b)可知，随着转矩的增大，节点6(d)的振动响应幅值并非像节点5(c)的振动响应幅值那样先大幅度降低再趋于相对稳定，而是其响应幅值一直维持在相对稳定的状态，由此可知，滚动联轴器能较好地隔离不利振动在轴系间的传递,有利于多跨度系统的稳定运行。

图7 轴心轨迹图

图8 时域响应

5 结 论

本文根据滚动联轴器啮合数学模型，推导了滚动联轴器的刚度系数和阻尼系数的数学表达式，并采用总体耦合矩阵法，建立了滚动联轴器-转子耦合系统的振动方程。结合实例，计算分析了不同转矩情况下联轴器—转子耦合系统中联轴器的动态特性规律，得到了如下结论：

1)在低转矩高速传动中，滚动联轴器耦合力弱，对转矩大小敏感，其传动性能不佳，但随转矩增大，联轴器耦合力增强，其振幅急剧降低，能快速地调整到稳定传动状态；

2)在大转矩高速工况下传动时，滚动联轴器的振幅变化幅度较小，表现良好的传动稳定性，并且随着转矩的增大，幅值变化也逐渐减少，最后趋于稳定，能较好的适应非稳定转矩的重载系统；

3)滚动联轴器的左、右半联轴器相互间的振动幅值影响很小，能较好的隔离不利振动的传递，有利于多跨度系统的稳定运行。

参考文献：

[1]刘占生,赵广,龙鑫.转子系统联轴器不对中研究综述[J].汽轮机技术,2007,49( 5 ) : 321-325.

[2]BROMM U E,KRMER E.Instability and self-excitation caused by a gear coupling in a simple rotor system [J].Forsch Ingenieurwes,2006,70: 25-37.

[3]HUSSAIN A K M.Dynamic stability of two rigid rotors connected by a flexible coupling with angular misalignment[J] .Journal of Sound and Vibration,2003,266: 217-234.

[4]徐海良.滚动联轴器:中国,200410047030.4 [P].2005-06-08.

[5]徐海良,何清华.轴向可移动联轴器:中国,200420036073.8[P].2006-06-28.

[6]徐海良,何清华.滚动联轴器研究[J].中南工业大学学报，2000,5 (31)：454-457．

[7]XU HAILIANG,HE QINGHUA.Design and application of a new kind of rolling coupling[J].J Cent South Univ Technol,2005,12(3)：335-339.

[8]徐绍军,徐海良.齿轮联轴器与滚动联轴器对比研究[J].机械设计与研究,2007,23 (3)：87-90.

[9]LI M,YU L.Analysis of the coupled lateral torsional vibration of arotor-bearing system with amisaligned gear coupling[J] .Journal of Sound and Vibration,2001,243( 2) : 283-300.

[10]徐海良，龚姚腾.滚动联轴器设计理论及方法[J].南方冶金学院学报,2001,22 (4)：264-267.

[11]JOHNSON K L.Contact mechanics[M].England:The Press Syndicate of the University of Cambridge,1985.

[12]虞烈,刘恒.轴承—转子系统动力学[M].西安: 西安交通大学出版社,2004.

[13]CALISTRAT M M.Friction between high speed gear coupling teeth[J].ASME Journal of Mechanical Design,1981,103(1):54-60.

[14]赵海呜,徐海良.滚动联轴器与滚珠联轴器的摩擦性能分析[J].凿岩机械气动工具.2006,3：28-34.

[15]范叶森,王三民,杨振.挠性联轴器耦合多转子系统振动分析的总体耦合矩阵法[J].机械科学与技术,2010,5(29)：584-588.

[16]张海燕，段元明.参数激励电磁轴承-转子系统的混沌特性研究[J].中山大学学报:自然科学版,2003,42(2):127-129.

[17]XU M,MAZANGONI R D.Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance[J].Theoretical Model and Analysis,Journal of Sound and Vibration,1994,176:663-679.