基于白化权函数的改进区间灰数预测模型

丁婳婳

(华北水利水电大学 数学与统计学院，河南 郑州 450046)

0 引言

灰数及其运算是灰色系统理论的基础。灰数是指仅知道取值范围但不知其确切值的数，用记号“⊗”表示[1]。

文献[2]根据区间灰数的已有分布信息发掘其几何意义，并把灰数序列转换为实数序列完成建模预测，但仅能解决典型白化权函数类型。文献[3-4]从区间灰数的“核”“信息域”以及“认知程度”等特征出发实现预测；文献[5]利用文献[3-4]定义的信息域和认知程度，构建了改进的区间灰数预测模型；区间灰数的标准化形式在文献[6]中给出，文中把区间灰数分为“白部”和“灰部”两个实数序列；文献[7]中对文献[6]所定义的两个实数序列分别进行预测，进而完成区间灰数的预测；文献[8]在文献[7]的基础上又运用函数的面积和重心给出白化权函数预测模型；文献[9]基于核与测度完成了区间灰数的预测；文献[10]为了保证灰度在建模过程中不减，利用准灰度因子对区间灰数取值范围进行灰度最大化处理；文献[11]在“灰度不减”公理条件下，定义两组含上下限信息的核序列的预测模型降低误差;文献[12]和文献[13]分别提出了基于白化权函数的灰数的核与灰度的定义。

本文将利用文献[12-13]给出的定义，完成基于白化权函数的区间灰数的预测。根据已有信息，本文通过充分利用白化权函数端点值与区间灰数的边界值之间的关系，建立预测模型。最后将模型应用于已有文献的算例分析中，验证了模型的有效性和实用性。

1 基本概念

定义1[2]既有下界ak，又有上界bk的灰数称为区间灰数，记为⊗k∈[ak,bk]，其中ak≤bk，k=1,2,…。由区间灰数构成的序列记为X(⊗)=(⊗1,⊗2,…,⊗n)。

定义2[1]对于区间灰数⊗k∈[ak,bk],ak≤bk，k=1,2,…，在缺乏灰数取值信息分布情况下称

(1)

为区间灰数的核。

定义3[4]对于区间灰数⊗k∈[ak,bk],ak≤bk，k=1,2,…，称区间长度

d(⊗k)=bk-ak

(2)

为区间灰数的信息域。X(⊗)中所有区间灰数的信息域构成的序列称作信息域序列，记为

Xd=(d1,d2,…,dn)。

定义4[3]对于区间灰数⊗k∈[ak,bk],ak≤bk，k=1,2,…，称

(3)

Xp=(p1,p2,…,pn)。

定义5[13]用来描述一个灰数⊗k∈[ak,bk]在其取值范围[ak,bk]内对不同数值的偏好程度的函数，称作区间灰数⊗k的白化权函数，记为f⊗k(x)；起点、终点确定的左升、右降连续函数称为典型白化权函数，如图1所示。

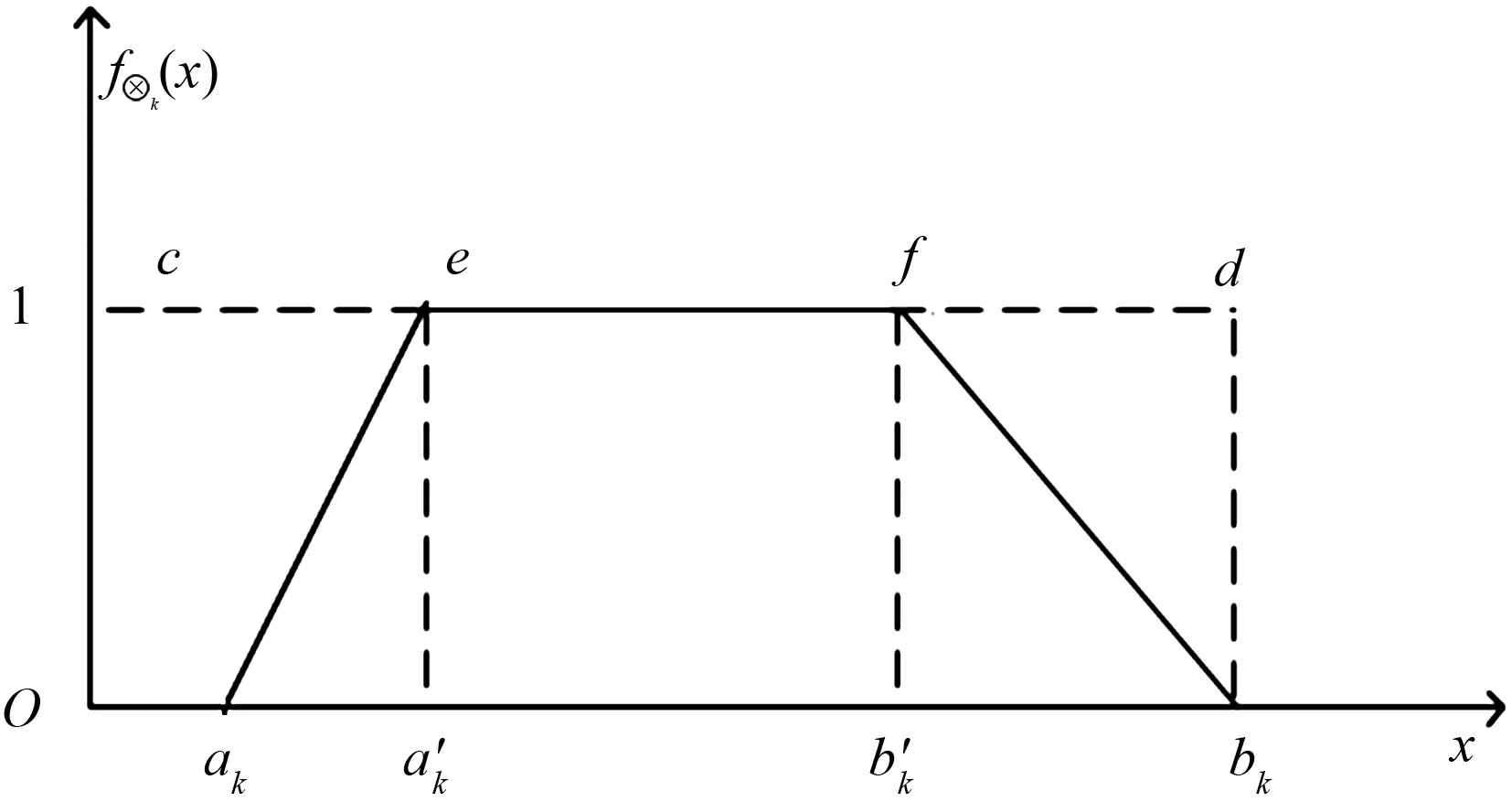
图1 典型白化权函数Fig.1 Typical whitening weight function

定义6[13]图1中，当a′k=b′k时，则称函数为三角白化权函数，如图2所示。

图2 三角白化权函数Fig.2 Triangular whitening weight function

定义7[12]论域Ω∈[a,b]，区间灰数⊗k∈[ak,bk]⊂Ω，k=1,2,…，f⊗k(x)为灰数⊗k的白化权函数，且0≤f⊗k(x)≤1，则区间灰数的核为

(4)

定义8[13]一种基于灰色白化权函数的灰数灰度定义(如图1)

(5)

2 基于白化权函数的改进区间灰数预测模型的构造

基于白化权函数的改进区间灰数预测模型的建模流程：首先根据已有的信息内容，计算出区间灰数的信息域和认知程度序列，对两序列依次建立DGM(1,1)模型，经由推导还原，完成区间灰数上下界值的预测；因为已知各区间灰数的白化权函数，就已知其在取值区间内的偏好信息，故在计算认知程度时，用文献[12]给出的核来作为白化值。然后根据核与灰度，建立白化权函数端点值与区间灰数的上下界信息之间的关系，通过对核与灰度序列建立GM(1,1)模型再推导，完成白化权函数端点值的预测。

2.1 白化权函数已知的区间灰数上下界预测

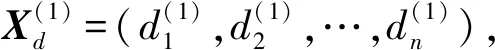
其中k=1,2,…,n，

且

其还原值为

(6)

其中k=1,2,…，n。

同理建立认知程度序列的DGM(1,1)模型，还原值为

(7)

其中k=1,2,…,n。

由于此时缺乏预测值的取值分布信息，故用式(1)给出的核作为认知程度中的白化值。有

(8)

且

(9)

联立式(8)和式(9)可得

(10)

将式(6)和式(7)的预测结果代入式(10)中即可得区间灰数上下界的预测值。

2.2 白化权函数端点值预测

基于白化权函数的区间灰数预测模型，在预测完区间灰数的取值范围基础上，完成白化权函数端点值的预测。本文研究了两种白化权函数类型。

1)白化权函数为典型白化权函数。

当f⊗k(x)为典型白化权函数时，如图1所示，其具体表达式为

由式(4)可求得区间灰数的核为

(11)

由式(5)可得区间灰数的灰度

(12)

对核与灰度序列分别建立GM(1,1)模型，其还原值为

(13)

(14)

已知区间灰数的核与灰度的预测值，联立式(11)和式(12)，将式(13)和式(14)的结果代入即可得典型白化权函数端点预测值的表达式，为

(15)

(16)

由式(15)和(16)即可得典型白化权函数的端点预测值。

归纳建模步骤：

步骤1通过式(2)式(3)计算出区间灰数的信息域和认知程度，形成信息域序列和认知程度序列,认知程度中的白化值由式(4)给出；

步骤2通过式(6)和(7)对两个实数序列建立DGM(1,1)模型；

步骤3通过式(10)可还原得区间灰数预测值的上下界；

步骤4通过式(11)和(12)求出各灰数的核与灰度，形成核与灰度序列；

步骤5通过式(13)和(14)对核序列与灰度序列建立GM(1,1)模型；

步骤6通过式(15)和(16)可得典型白化权函数端点预测值；

步骤7模型精度分析。

2)白化权函数为三角白化权函数。

当f⊗k(x)是三角白化权函数时，如图2所示，其具体表达式为

由式(4)可得区间灰数的核为

(17)

由式(17)可得三角白化权函数端点值的表达式为

(18)

通过式(17)求出核，并形成核序列。通过式(13)可得区间灰数的核预测值。将上下界预测值和核预测值代入式(18)即可得三角白化权函数的端点预测值。

归纳建模步骤：

步骤1-3同1)；

步骤4通过式(17)求出所有灰数的核；

步骤5通过式(13)对核序列建立GM(1,1)模型；

步骤6通过式(18)得到三角白化权函数端点预测值；

步骤7模型精度分析。

3 算例分析

为了便于比较模型精度，本文引用文献[8]的数据进行建模，并将结果进行对比分析。文献[8]收集了黄河巴彦高勒站2008—2013年在凌期12月09日到第二年3月15日的日均流量，原数据见表1。可转化为基于三角白化权函数的区间灰数，如表2。

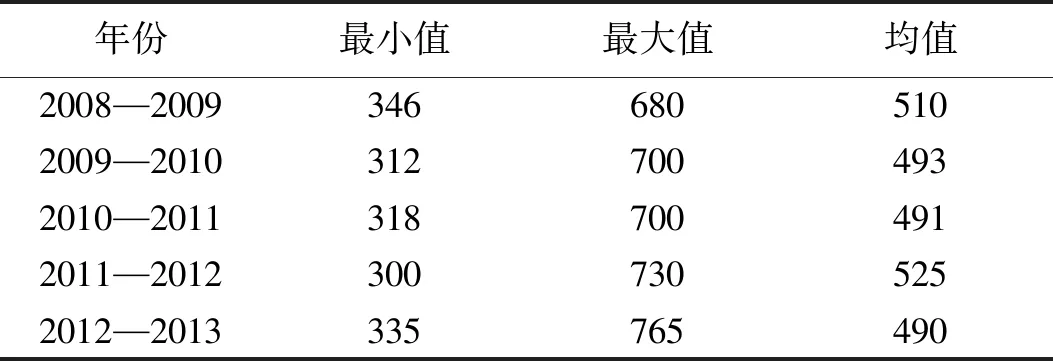
表1 巴彦高勒站2008—2013年凌期日均流量/m3·s-1Tab.1 Daily average flow rate of Bayangola Station during ice age from 2008 to 2013/m3·s-1

表2 巴彦高勒站2008—2013年凌期日均流量/m3·s-1Tab.2 Daily average flow rate of Bayangola station during ice age from 2008 to 2013/m3·s-1

根据2008—2012年的数据，建立模型预测2012—2013年的日均流量，步骤如下：

步骤1通过式(2)式(3)计算出区间灰数的信息域和认知程度，得到信息域序列和认知程度序列

步骤2通过式(6)和(7)对两个实数序列建立DGM(1,1)模型得

步骤3通过式(10)可得区间灰数预测值的取值区间为[312.41,780.9]；

步骤4通过式(17)求出的核序列为

步骤5通过式(13)对核序列建立GM(1,1)模型为

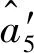
步骤7模型精度分析,将本文模型预测结果与文献[8]方法的预测结果对比见表3。

表3 两种方法模拟预测值对比分析

4 结论

本文通过区间灰数的已有信息计算出各特征值，先计算出信息域与认知程度序列，对两序列建立DGM(1,1)模型，经由推导还原得区间灰数预测值的上下界；再根据核与灰度，建立白化权函数端点值与上下界信息之间的关系，通过推导还原，来完成白化权函数端点值的预测，研究了两种白化权函数类型。 并将本文模型应用到已有文献的算例分析中，结果表明本文所提出的预测模型模拟精度较好。但本文的白化权函数都是线性函数，当白化权函数为非线性函数时要做出怎样的改进，这是接下来研究的重点。