一种探测和修复周跳的新组合方法＊

赵庆志，张书毕

（1.中国矿业大学 环境与测绘学院，江苏 徐州221008；2.江苏省资源环境信息工程重点实验室，江苏 徐州221008）

0 引 言

在GPS载波相位测量中，周跳的探测修复和整周模糊度的确定始终是两个核心问题。载波相位实际观测值由不足一周的小数部分和整周部分组成。不足一周的小数部分可以精确地获得，整周部分由多普勒计数器累计。在整个观测时段，如果整周计数不产生错误，则相位观测值初始模糊度保持不变。因此从数据处理角度来看，即使解算不出模糊度，仍可用实数解和三差解，只是精度不如固定解高而已。如果无法探测出周跳，观测值中就会含有偏差，也就无法获得正确的结果［1］。

卫星在空间的运行轨迹是一条平滑的曲线，因而卫星至接收机的距离观测值的变化也是平缓而有规律的。周跳将破坏这种规律性，使观测值产生一种系统性的粗差。周跳的探测及修复本质上讲就是如何从载波相位观测值的时间序列中寻找出可能存在的这种系统性的粗差并加以改正［1］。

目前常用的周跳探测方法有许多［2－11］，但都有自己的优缺点。例如电离层残差法根据伪距相位检测量判断周跳是否存在，不足之处在于没有解决周跳解的多值性问题；多项式拟合法一般只能发现较大的（一般大于5周）周跳。每种方法都有自己的不足之处，在提高GPS定位精度方面存在一定的局限性。因此在充分利用电离层残差法和相位减伪距法优点的基础上提出了一种新的探测和修复周跳的方法。

1 电离层残差法

电离层残差法由Goad提出，基本思想是使用双频载波相位测量的电离层残差组成电离层残差检测量，并根据检测量在历元间的变化探测是否存在周跳。

L1和L2的载波相位观测方程分别为

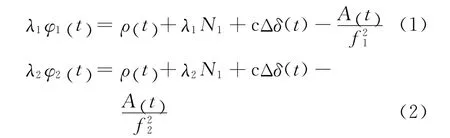
式中：λ1、λ2分别代表L1、L2的波长；N1、N2分别代表L1、L2的模糊度；φ1（t）、φ2（t）分别代表L1、L2的相位观测值；f1、f2分别代表L1、L2的频率；c代表光速；Δδ（t）代表t时刻的接收机钟差；ρ代表卫星至接收机间的真正距离。

构造电离层残差检测量Φ（t）［2］

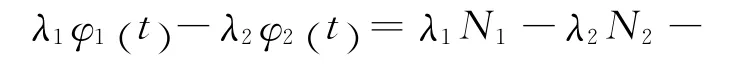
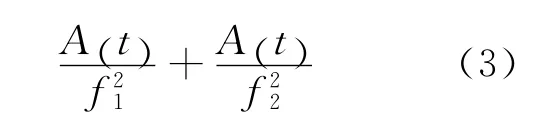
上式两边同除以λ1并利用关系式得

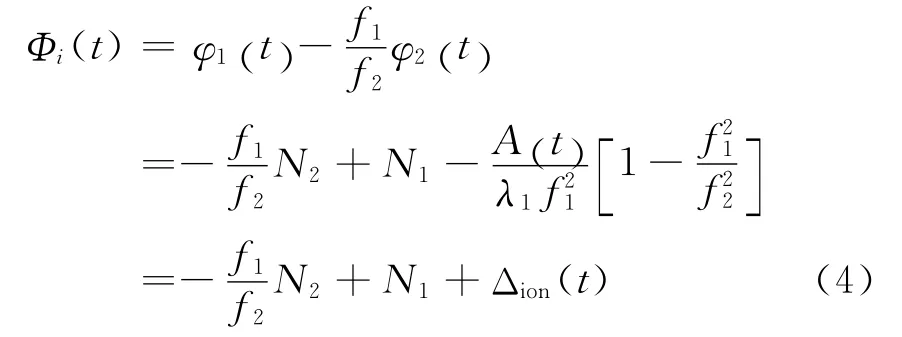
若不存在周跳，历元间的Φi（t）之差为

若L1和L2的周跳分别为ΔN1和ΔN2，则有

A （t） 为电离层延迟的变化量，当电离层比较稳定，采样率高且没有周跳存在的情况下，历元间电离层残差检测量的变化值Φi（t，t＋1）在零附近波动。但当有周跳存在时，Φi（t，t＋1）的值就会有跳变。

对式（6）应用误差传播定律可得

假设L1和L2的测量误差均为：mφ＝±0.01周，则有：mΔΦ＝±0.023周，按三倍中误差为限差，可知限差为±0.07周，也就是当两个载波上的周跳引起的历元间电离层残差检测量变化值大于0.07周时，才能将L1和L2上的周跳分离开［3］。

2 相位减伪距法

伪距观测值不含整周模糊度，一般认为它不受周跳影响。基本思想是根据伪距和载波相位观测方程，在相位观测值和伪距观测方程之间作差，消除卫星钟和接收机钟差的影响。

伪距观测方程和载波相位观测方程分别为

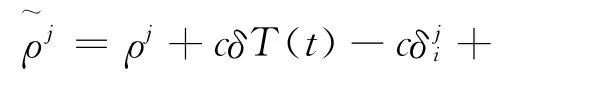
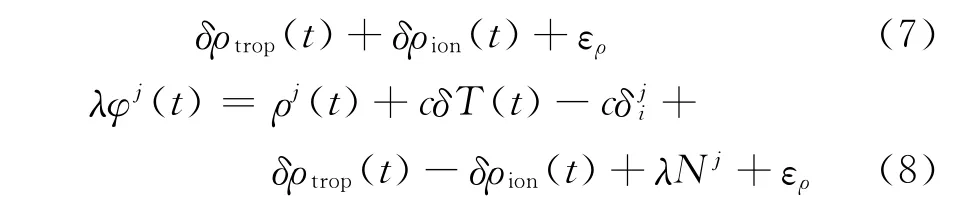
式中，δρtrop、δρion分别表示对流层、电离层误差。

由观测方程（7）和（8）可知，测码伪距观测方程不含模糊度项，因此，可认为它不受周跳的影响；对于载波相位观测值和测码伪距观测值而言，除电离层延迟影响、多路径效应和测量误差外，其他误差影响相同。将式（7）减去式（8）得

将式（9）在历元间求差，可得相位减伪距法的检测量［4］：

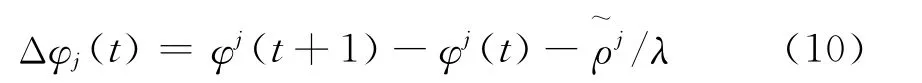
检测量Δφj（t）与载体的运动状态无关，可用于静态或动态测量中非差、单差或双差载波相位观测值的周跳检测，且只能探测和修复大的周跳。

3 联合利用电离层残差法和相位减伪距法探测和修复周跳的原理

基于相位减伪距法能够探测大周跳和电离层残差法对小周跳异常敏感这种特点，我们联合应用电离层残差法和相位减伪距法，将这两种方法进行合理组合，使之互相弥补，并结合实际数据，对其算法进行实现。

具体步骤：

1）利用相位减伪距法探测出观测值中的大周跳（通常大于7周）；

2）利用电离层残差法对小周跳异常敏感这种特点，探测出产生周跳的历元，并将其标记，计算出可能存在的周跳值；

3）将标记了的历元的载波的周跳值回代加上上一步计算出的周跳值，在利用相位减伪距法来判断是否真的产生了周跳，从而将小周跳分离出来。

4 实例分析

为检验利用电离层残差法和相位减伪距法这种组合方法探测和修复周跳的效果，对采集的观测数据进行分析和处理。

图1为由干净的实测1s采样率数组组成的无周跳电离层残差图。

在50历元处分别在L1载波和L2载波上加上5和－3周跳，组成电离层检验量输出，如图2所示。

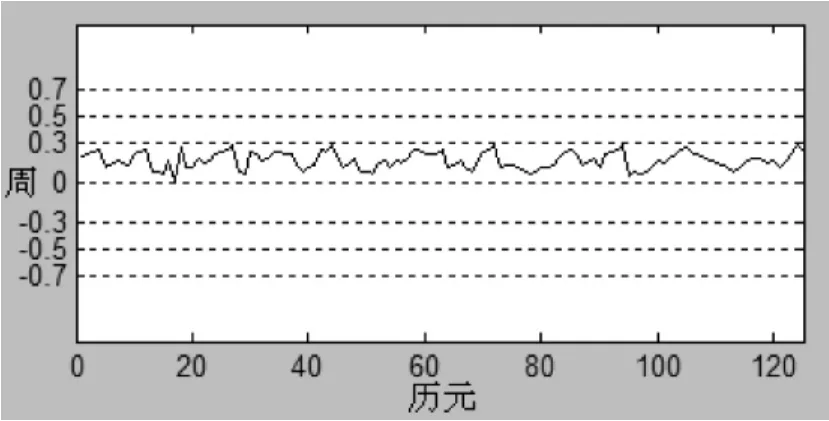
图1 无周跳电离层残差图

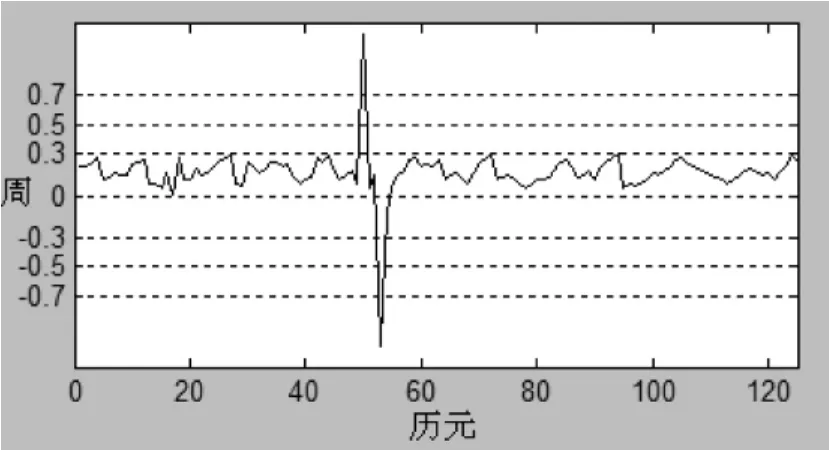
图2 有周跳的电离层残差图

电离层残差法对小周跳异常敏感，但是不能判断出是否真的存在周跳。而伪距观测值不含整周模糊度，一般认为它不受周跳影响。所以可以利用相位减伪距法检验所选取的周跳值是否是真正的周跳值。此时可以把ΔN1＝5和ΔN2＝－3回代到相位减伪距的检验量中，其结果如图3和图4所示。由以上实例可以证明ΔN2＝－3是正确的周跳值，而ΔN1＝5不是。组合使用这两种方法可以实现周跳的唯一分离。

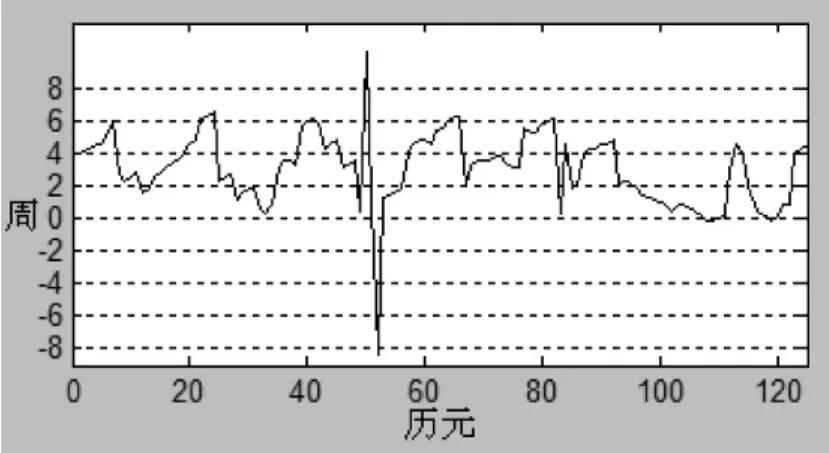
图3 ΔN1＝5回代到相位减伪距的检测量有周跳

图4 ΔN2＝－3回代到相位减伪距的检测量无周跳

5 结 论

1）联合利用电离层残差法和相位减伪距法探测与修复周跳的方法充分利用了这两种方法的优点，互相补充，将电离层残差法的分辨能力从4周提高到了8周，有效地解决了周跳解多值性的问题；

2）利用电离层残差法和相位减伪距法探测周跳不需要测站、卫星轨道等信息，基线长度对其也没有影响，能探测出1周以上的周跳，且能唯一分离出不同频率的周跳。不足之处在于这种方法依赖于单个接收机的双频相位和伪距观测数据，因此该方法只适合于双频接收机。

此外，该方法原理简单，计算速度快，是一种较好的探测和修复周跳的方法。

［1］ 李征航，黄劲松.GPS测量与数据处理［M］.武昌：武汉大学出版社，2005

［2］ 韩绍伟.GPS组合观测值理论及应用［J］.测绘学报，1995，24（2）：8－13

［3］ 刘根友，朱才连，任 超.GPS相位与伪距联合实时定位算法［J］.测绘通报，2001（10）：10－11.

［4］ 何海波.高精度GPS动态测量及质量控制 ［D］.郑州：解放军信息工程大学，2002：36－42.

［5］ 阳仁贵，欧吉坤，袁运斌.一种GPS相位周跳分段平均组合的自动修复方法［J］.大地测量与地球动力学，2009（5）：76－80.

［6］ 王 威，隋立芬，符 养，等.综合利用双频观测值进行周跳的探测与修复［J］.海洋测绘，2006，26（5）：24－27.

［7］ 生仁军.GPS载波相位定位中周跳探测方法的研究［D］.南京：东南大学，2006.

［8］ 刘伟平，郝金明，汪 平，等.Kalman滤波在周跳探测与修复中的应用［J］.大地测量与地球动力学，2009（6）：101－103.

［9］ 伍 岳.第二代导航卫星系统多频数据处理理论及应用［D］.武昌：武汉大学，2005.

［10］ ALTMAYER C.Ehancing the integrity of integrated GPS／INS system by cycle slip detection and correction［C］／／Proceedings of the IEEE Intelligent Vehicles Symposium Dearborn，Miami，October 3－5，2000.

［11］ DEDES G.Effects of the ionosphere and cycle slips in long baseline dynamic positioning［C］／／Proceedings of Mobile Mapping Symposium，Columbus，O－hio，May 44－26，1995.