载波相位测量技术研究＊

2012-04-26李炜

全球定位系统 2012年3期

李炜

（61081部队，北京100094）

0 引言

载波相位测量技术是目前高精度定位的主要方法［1］。载波相位测量可以达到毫米级的精度，但测量值受到与码测量同样的误差源的影响：卫星钟差和星历误差、传播媒介、接收机噪声和多路径。码测量和载波相位测量的主要差别在于接收机噪声和多路径的影响，载波相位一般在厘米级而码相位在米级，另外，载波相位测量存在整周模糊度。如果所有的误差项都被减小，整周模糊度能被解出来，载波相位测量将转化为精确的伪距测量值并形成精确定位估算。

利用载波相位测量的厘米级相位定位现已在测绘、大地测量、地球物理和很多工业应用领域得到了广泛的应用，载波相位测量中难点在于实时的、快速而准确的整周模糊度［2］。将对载波相位测量技术做一详细的研究，主要从实现原理和方法进行详细的论述。

1 载波测量接收机工作原理

载波测量是在接收机的载波跟踪环中实现，其中载波预检测积分器，载波环检相器和载波环滤波器的可编程的方案确定了接收机载波环的特性。它确定了接收机载波环方案的两个最主要的性能特性：载波环的热噪声误差和最大视距动态应力门限［3］。载波环电路如图1所示。

图1 接收机载波环工作原理图

载波环在工作时考虑到接收机最大视距动态应力等情况，往往由FLL（锁频环）和PLL（锁相环）组成，在PLL上输出相位误差，在FLL上输出频率误差。在实际工作中，FLL与PLL设计上有一定的冲突，如为提高接收机的动态应力，预检测积分时间应尽可能短，采用FLL，并将载波环滤波器的带宽设计宽些。为了使载波测量精度提高，预检测积分时间应长，鉴别器采用PLL，且载波环路滤波器的带宽取窄。为解决这个矛盾必须采用折中的方案。在实际接收机工作时，由FLL（锁频环）首先完成对接收信号载波的快速频率捕获，再由PLL（锁相环）完成对载波相位的精确跟踪，同时完成对载波相位的精确测量［3－4］。

环路滤波器的作用是降低噪声以便在其输出端对原始信号误差进行精确的估计，其设计的阶数和噪声带宽也决定了环路滤波器对信号的动态响应，如图2所示。

图2 载波环滤波器原理图

图2示出了1个2阶FLL和3阶PLL构成载波环滤波器，采用该方式构成的环路滤波器可以对存在的加速度等动态应力有很好的适应能力，在实际设计中经常被采用，通过调整滤波器内的各系数完成对滤波器指标的调整［5－7］。

2 载波测量原理

设卫星上某一时刻的载波相位为φ0，经过距离L后到达接收机时相位为φ1，那么载波所经历过的载波相位变化为（φ1－φ0），其中，包括整周数和不足一周的小数部分。

其测距公式为

式中：l为卫星到接收机的距离；λ为已知载波的波长；n0为载波相位（φ1－φ0）中的整周期数部分；φ为载波相位（φ1－φ0）中不足一周的小数部分；n0不能直接测量得到，即为载波测量中的整周模糊度，Δφ可以精确测量。如果从公式（1）中能确定n0，那么测距误差是很小。将其分别代入卫星时钟、接收机时钟和其它误差进行展开变换，可以得到载波相位测量的线性化方程

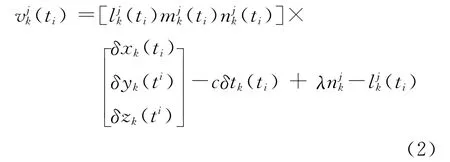
3 测量数据应用

载波测量的精度主要受PLL所测量出的载波相位的影响，反映到实际中为测量伪距的变化率。通过测量固定时间间隔内的载波相位变化量得到，其距离变化为

式中λ为载波波长。

在载波环和码环测量的分辨率相同情况下，由于载波频率远高于伪码频率，所以通过载波测量可以得到很高精度的测量量。一般可以得到微米级。载波测量定位技术中存在两个问题：整周模糊和整周跳变。根据式（2），公式中有3个位置未知量，1个时钟未知量和1个整周模糊量。由于在GPS系统中只有两个载波频率点，观测方程不能通过一次测量多颗卫星来求解，需要对多颗卫星进行多次测量。解决该问题的方法经历了从整周模糊数作为参数求解利用三差法和“停—走”法、两次设站求解法、快速模糊解算法等过程，仍然需要多次测量和计算实现。

在正在建设的伽利略系统中，由于采用3个以上的载波频率，可以很好地解决整周模糊问题。根据欧洲航天局提出的使用3个载波解决整周模糊的TCAR方案，利用3个载波上的伪距观测方程和相位观测方程可以直接求出任意一个载波上的整周模糊度。并由此经过一次测量多个卫星来计算得到用户的位置信息。虽然载波相位的变化可以精确测量出来，但需要消除载波整周模糊情况，一般采用伪码观测量，将相应的载波相位观测量的中心定在以码的观测量的平均值上，再通过利用补充卡尔曼滤波器，最终完成载波测量数据的提取。

4 载波测量技术应用

差分定位技术是使用差分载波通过在两个地方使用两台接收机，其中一台位置精确已知，通过已知精确位置的接收机求得另一台在需要测量位置的接收机的较高精度位置数据。通过差分技术可以基本消除电离层的影响，至少在使用差分GPS的相对地理区域较小的情况下，例如，在机场和港湾中使用。也可以利用广域差分技术实现在一个较大地区完成差分定位服务，以提高该地区的定位精度。

同时产生载波相位和伪距码双差是测定两个天线之间的基线矢量的关键，但卫星星历必须作一定的处理，以保证在两个接收机位置上所作的载波相位和码测量相对GPS系统时调到一个共同测量时基上。双差的形成具有极大的好处，因为这样能最终对消掉接收机和卫星时钟的偏差极大部分的电离层传播延迟。如果两个天线位于同一高度，对流层延迟也会大部分对消掉。

如图3所示利用GPS干涉仪对一颗卫星进行载波测量，其干涉测量量，即单差（SD）现在通过两条载波周传播路径长度（卫星p分别到干涉接收机k和m）之差来产生

通过上式可以得到，在形成单差量度中产生了一些好处，主要是：消除了卫星发射信号相位和时钟偏差，并形成一个合并的整数多项式，该项表示从m到k在mp视线上的投影点的载波整周数。合并的相位噪声值以及合并的接收机时钟偏差项也已建立。

如果把GPS干涉仪扩展到两颗星，则可完成第2个单差测量度

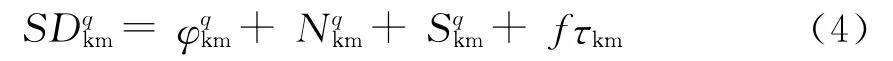
将（3）与（4）相差得

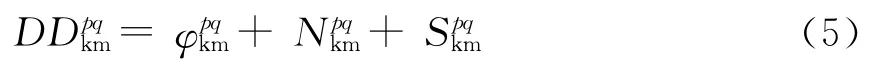
图3 双差测量原理图

当形成双差时，接收机时钟偏差抵消掉了，剩余的是相位项、整数项和系统相位噪声项，相位项表示由接收机在k和m处用卫星p和q所作的合并载波相位测量，整数项由合并的未知整数多值性组成，而系统相位噪声项主要由合并的多径和接收机影响组成。将余下的误差与存在于两个接收机天线之间的未知基线b相关联起来，可以得到以下方程

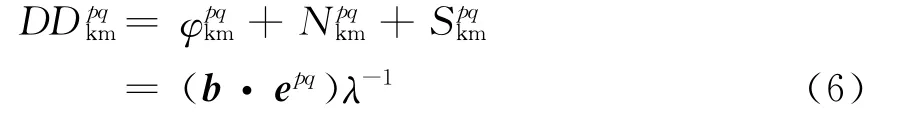
式中：b·epq是未知基线矢量和至卫星p和q的单位矢量之间的内积。

如果继续增加观测卫星的数量，其它噪声也可以对消掉，利用5颗以上的卫星可以产生4个独立的双差方程，由方程（6）对4个双差作变换和展开如下

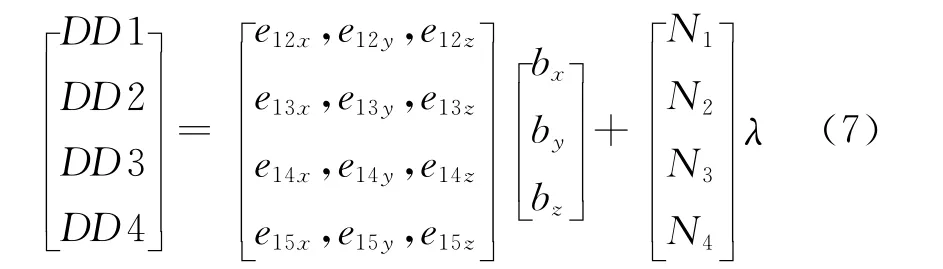
式中：DD为4个独立双差；e是考虑两颗卫星之间的单位矢量之差；b是基线矢量；N是相关联的载波整周模糊性；λ为所用载波波长。

通过以上介绍的方法可以得到载波测量的双差，提高了载波伪距测量精度，由于还可能存在多值性，所以需要与码的双差测量同时使用（码的双差测量与载波双差测量相似）来产生平滑的码双差测量值，采用卡尔曼滤波器等技术手段完成高精度测量任务，使测量精度达到厘米级甚至毫米级，以满足不同用户的精度要求。

为了验证载波相位的高精度定位性能，在北京地区做了载波相位测量实验，在距离37km的两个已知点上，分别架设双频GPS接收机，采集载波相位观测值约4h，采样间隔1s.

两个已知点坐标精确已知，利用其中一个已知点作为基准站，另一个已知点作为流动站，利用载波相位测量值和上述差分定位算法，单历元解算流动站坐标，并与已知点精确坐标进行比对，转化为站心坐标系，定位误差如图4～6所示。

图4 载波相位测量N方向误差

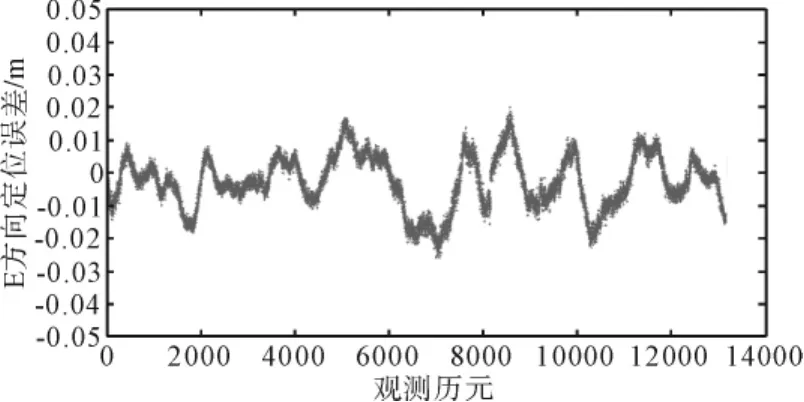
图5 载波相位测量E方向误差

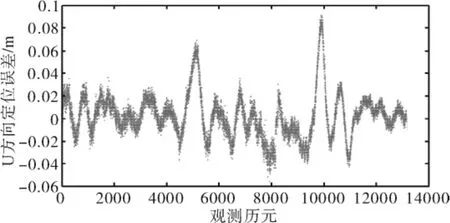
图6 载波相位测量U方向误差

经统计，N方向误差最小值为－0.041m，最大值为0.032m，平均值为0.001m，标准差为0.012m；E方向误差最小值为－0.026m，最大值为0.02m，平均值为－0.001m，标准差为0.008m；U方向误差最小值为－0.056m，最大值为0.091m，平均值为0.003m，标准差为0.02m.

统计结果表明：载波相位差分定位单历元能够达到厘米级精度。