GPS卫星轨道精度对定位结果的影响＊

杜 娟，刘 星，陈正阁

（63883部队，河南 洛阳471000）

0 引 言

GPS信号能够高精度、全天候的测量运动载体的七维状态参数和三维姿态参数，为测控设备的高精度鉴定提供了一种新技术。GPS精度鉴定系统可以在大空域范围内提供高精度的标准比对数据，不受天气影响、易于实施、经济实效。卫星导航系统中卫星作为动态基准，星历误差作为起算数据误差，严重影响单点定位的精度，也是精密相对定位中的重要误差源［1］。

目前高、中精度无线电外测设备的GPS精度鉴定，是通过飞行试验或专门的鉴定试验，评定测控设备的精度及数据的不准确性，检验测控设备是否达到预期的设计指标并给出置信度，确定测控设备的随机误差和系统误差，为改善、提高测量系统精度提供依据，测控设备的精度鉴定，是确保和提高测控设备精度的基础，具有重要的作用和意义。

在轨道精度、表示方式和实时性等方面对广播星历、超快速星历、快速星历和精密星历进行了比较分析，并研究了不同星历对定位精度的影响。

1 卫星星历

1.1 广播星历

根据美国GPS控制中心跟踪站观测数据进行拟合外推得到广播星历，由GPS卫星发布、用户接收机可实时获取的一种预报星历。GPS广播星历的轨道参数由16个元素组成，每一颗卫星的广播星历每天更新一次，或者在用户距离误差（URE）超过规定的限值时更新。由于人造地球卫星绕地球运行时，除了受地球重力场的引力作用外，还受到太阳、月亮和其他天体引力影响，以及太阳光压、大气阻力和地球潮汐力等因素的影响，目前还不能充分了解作用在卫星上各种摄动因素的大小及其变化规律，预报星历存在较大的误差［2］。

1.2 IGS服务及轨道产品

国际大地测量协会为支持大地测量和地球动力学研究于1993年组建了国际GPS服务组织（IGS）。IGS由七个数据分析中心（AS）和分布在世界各地的数百个跟踪站组成，数据分析中心分别采用不同的定轨软件和方法确定卫星精密星历、保持地面参考框架、研究电离层的变化和确定地球自转参数，将各自的结果按加权平均的方法得到最终结果并发布［3］。

目前，IGS向全球用户提供各跟踪站GPS观测资料和IGS的各种产品，就星历而言IGS产品包括：预报星历、超快速星历、快速星历和精密星历，数据格式为SP3，卫星轨道属于ITRF参考框架［4］。

从2000年3月10日开始，IGS中央局推出了一种新的轨道产品IGU轨道。每个IGU星历文件轨道弧长48h，前24h是基于实测GPS数据的精密轨道，后24h则是预报轨道。由各分析中心独立产生各自的IGU轨道，数据中心确定各分析中心轨道的权，最后形成综合IGU轨道。IGU轨道每天发播两次，分别在UTC时3：00和15：00发布，因此用户只需在3h之后即可获取。同时，由于该轨道有24h的预推轨道，也可作为实时使用［5］。IGR星历是由IGS提供的快速星历，各分析中心在收集全球IGS监测站数据时，由于各监测站通讯的影响，采用的观测数据比计算精密星历时少，在17h之后即能获取，可用于后处理。IGS精密星历是为满足大地测量、地球动力学研究等精密应用领域的需要而研制、生产的一种高精度的事后星历。IGS精密轨道综合了7个分析中心的解，给出15min等间隔点上的卫星位置，在13天之后才能获取，精度约3～5cm.IGS精密星历可作为“真值”用以分析其他星历精度。

2 卫星轨道计算

广播星历采用开普勒根数和开普勒轨道摄动的调和系数及长期漂移项来描述，在GPS定位计算中，需要多次计算卫星位置和速度。如果用广播星历直接计算，需要占用较多的内存空间和计算时间。GPS卫星轨道是一个随时间连续变化的，可将卫星星历表示为时间的函数，即将一定时间间隔的卫星坐标用多项式进行拟合，以便在需要计算任意时刻卫星位置时，提高计算效率。IGS发布的星历产品直接提供规定时间间隔点上的卫星位置和速度，根据星历表，可借助插值公式，内插出任意时刻的卫星坐标。

2.1 切比雪夫轨道拟合［6］

对比各种多项式，切比雪夫多项式的逼近效果最佳，即使在时间段的两段近似性也很好。假设需要在时间间隔［t0，t0＋Δt］计算n阶切比雪夫多项式系数。其中t0为起始历元时刻，Δt为拟合时间区间长度。

将变量t∈［t0，t0＋Δt］变换成τ∈［－1，＋1］

则卫星坐标X，Y，Z的切比雪夫多项式为

式中CXi，CYi，CZi分别为X坐标分量、Y坐标分量、Z坐标分量的切比雪夫多项式系数。根据如下递推公式确定Ti（τ）

以X坐标分量为例，设Xk为观测值。则误差方程为

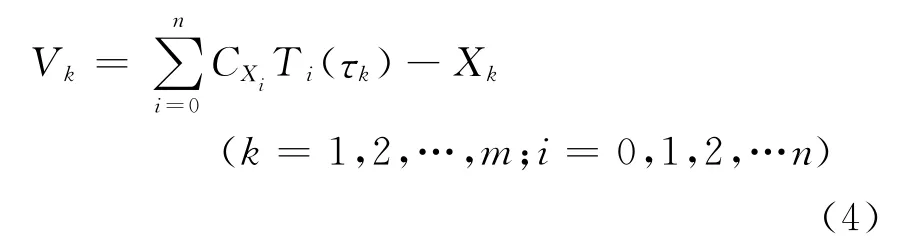
利用最小二乘原理求得关于某一GPS卫星在时间区间［t0，t0＋Δt］内各坐标分量的切比雪夫多项式拟合系数，利用式（1）、（2）、（3）即可计算时间区间内任意时刻卫星坐标。

2.2 拉格朗日插值

IGS提供的卫星轨道是固定时间间隔的卫星位置，根据这些离散点值，可借助格朗日插值公式，求出离散点之间任意时刻的卫星位置。

设在时间轴的n＋1个节点上的卫星钟差依次为x1（t1），x2（t2），…，xn＋1（tn＋1），则t时刻的函数值的插值公式为

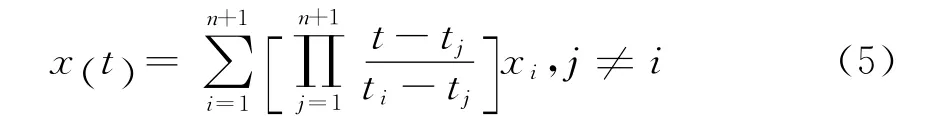
对于等间隔情形

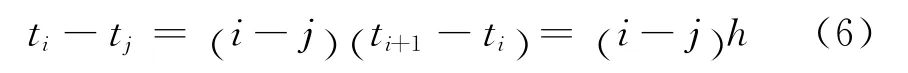
记

则式（5）为

式（8）对t求导数，可得速度

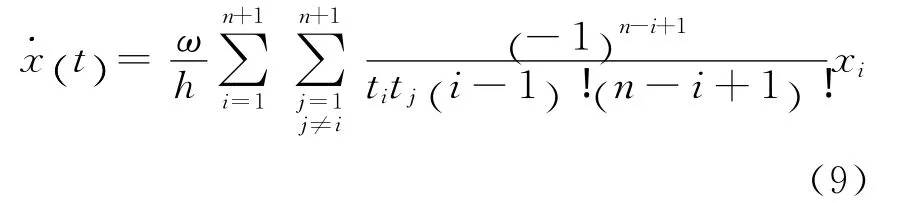
用拉格朗日内插公式插值的精度与插值点相对节点的位置有关，为得到较好的插值精度应依据插值点选择适当的节点。当插值点位于两端节点中央时精度最好［7］。

3 轨道精度比较

选取2008年11月12日所有在轨卫星的星历数据，分别将广播星历、超快速星历、快速星历的卫星轨道与精密星历的精密轨道进行比较，给出每一颗卫星在R、T、N方向上的轨道误差统计值。比较方法：

1）由广播星历计算卫星位置，利用12阶切比雪夫公式进行拟合；

2）利用8阶拉格朗日插值公式对IGU、IGR、IGS进行内插，内插出30s间隔星历列表；

3）广播星历采用的是1984年世界大地坐标系（WGS－84），而IGS提供的卫星星历是基于国际地球参考框架而产生的［8］，ITRF是一个考虑地球极移、章动和岁差年平均结果的动坐标系，二者之间存在的平移量和微小转动角的差异，可以利用相应的坐标变换参数进行相互转换。

以30号星为例，表1中计算了卫星在R、T、N方向上的rms统计值以及总的轨道误差，P为位置误差。图1～3显示了30号卫星广播星历、超快速星历、快速星历的卫星轨道与精密星历在R、T、N方向上的rms统计值变化，以及总的轨道误差。

表1 30号卫星轨道比较精度统计

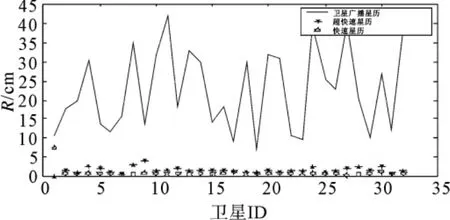
图1 R方向轨道误差变化

图2 T方向轨道误差变化

图3 N方向轨道误差变化

从以上图表可以看出，广播星历与精密星历所提供的卫星轨道相差较大，超快速星历居中，快速星历轨道与精密轨道非常接近。

4 轨道误差对定位精度的影响

GPS相对定位采用载波相位观测值为基本观测量，相对定位的结果是同步观测所得基线的三维坐标差。卫星轨道误差对相对定位的影响可按式（7）进行估算

其残余误差可求得

式中：ρ为观测站至所测卫星的距离；δρ为轨道相对误差；D为基线长；δD为由δρ引起的基线误差［9］。

例如，对于100km长的基线，取ρ＝22 000 km，δρ＝2m，相当于广播星历精度，则δD≈1 cm，对高精度的任务要求而言，这一误差不容忽视；所以，应综合考虑任务需求和成果提交的时间等情况，选择适当的卫星星历。

5 结 论

获得高精度定位结果是测控设备精度鉴定试验的前提，而卫星轨道误差是影响定位精度的重要误差源。它将直接影响绝对定位时所求用户接收机位置的精度，而在相对定位时，尽管卫星轨道误差的影响会减弱，但当基线较长、精度要求较高时，这种影响不容忽视。在测控设备高精度鉴定试验中，综合考虑试验精度要求、基线长短、成果提交时间等因素，选择最适合的GPS卫星星历，确保全航路高精度标准比对数据。

［1］ 李征航，黄劲松.GPS测量与数据处理［M］.武昌：武汉大学出版社，2005：47－53.

［2］ 刘基余.GPS卫星导航定位原理与方法［M］.北京：科学出版社，2006：319－329.

［3］ 常志巧.利用非差观测量确定GPS卫星轨道的方法研究［D］.郑州：解放军信息工程大学，2006（4）：1－3.

［4］ 吴显兵.星载GPS低轨卫星几何法定轨及动力学平滑方法研究［D］.郑州：解放军信息工程大学，2004（10）：14－20.

［5］ NEILA R E，MOORE A.International GPS service 2000：Life without SA［C］／／Proceedings of the 13th International Technology Meeting of the Satellite Division of the Institute of Navigation，Salt Lake，UT，2000：438－446.

［6］ 杨学锋，程鹏飞，方爱平，等.GPS卫星广播星历轨道误差突变分析［J］.全球定位系统，2008，33（4）：34－37.

［7］ 魏子卿，葛茂荣.GPS相对定位的数学模型［M］.北京：测绘出版社，1998：13－21.

［8］ 周忠谟，易杰军，周 琪.GPS卫星测量原理与应用［M］.北京：测绘出版社，1999：42－43.

［9］ HUGENTOBLER U，SCHAER S，FRIDEZ P.Bernese GPS software version 4.2［J］.Ed.Astronomical Institute／University of Bernese，2001：126.