分数阶积分微分方程三点边值问题解的存在性

朱彦，顾长超，吴婷，孙琳

（安徽大学数学科学学院，合肥 230039）

分数阶积分微分方程三点边值问题解的存在性

朱彦，顾长超，吴婷，孙琳

（安徽大学数学科学学院，合肥 230039）

利用Banach压缩映像原理和Krasnoselskii不动点定理，研究了一类分数阶积分微分方程三点边值问题解的存在性和唯一性.

分数阶积分微分方程；边值问题；存在性；唯一性；不动点定理

1 引言

近年来，分数阶微分方程初值问题和边值问题引起了广泛的关注.除了在数学领域的应用，还在光学和热学系统、流变学及材料和力学系统、信号处理和系统识别、控制和机器人等领域均有应用．随着分数阶微分方程理论知识的不断发展[[1-2]，关于分数阶微分方程解的相关性质的研究成果也层出不穷[3-8].但大多数仅仅是对分数阶微分方程的研究，随着分数阶微分方程在越来越多的科学领域里出现，从实际问题抽象出来的方程很有可能是较为复杂的含积分的分数阶微分方程，从而对分数阶积分微分方程的研究显得尤为迫切.

文献[3]和[4]讨论了分数阶积分微分方程边值问题解的存在性和唯一性.受其启发，本文研究了下面分数阶积分微分三点边值问题

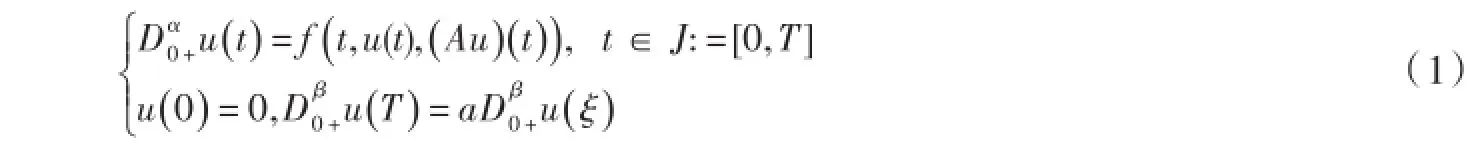
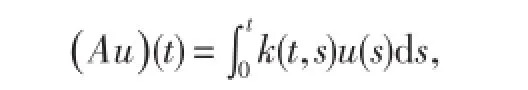
其中k∈(J×J,R+),另记

本文中我们首先给出有关分数阶微分方程的基本概念和准备知识；其次将边值问题（1）转化为等价的积分方程；最后，运用不动点定理得到解的存在性和唯一性的两个充分条件.

2 预备知识

定义2.1函数y:(0,+∞)→R的α阶Riemann-Liouville分数阶积分为

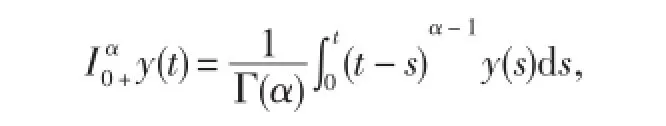
其中，α＞0，Γ(⋅)为gamma函数，右边在(0,∞)上是逐点定义的.

定义2.2函数y:(0,+∞)→R的α阶Riemann-Liouville分数阶微分为

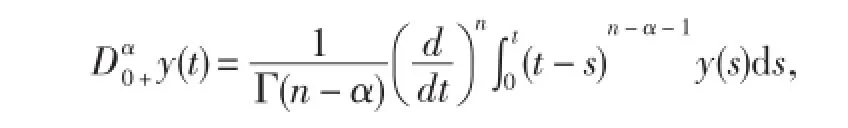
其中，n=[α]+1,[α]表示α取整，右边在(0,∞)上是逐点定义的.

引理2.3若u∈C(0,1)⋂L(0,1)有α阶导数属于C(0,1)⋂L(0,1)，则

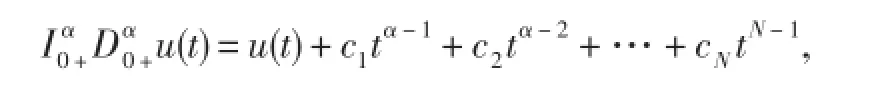
ci∈R,i=1,2,…,N,其中N=[α]+1.

引理2.4[6]假设函数h∈C(J,R),则函数u是分数阶积分方程

的解，当且仅当u是下述分数阶边值问题

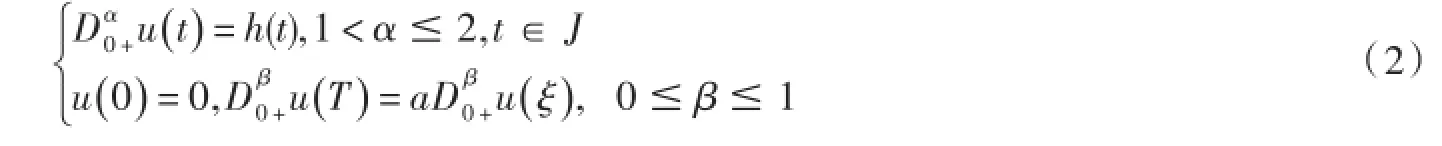
的解，其中d=(Tα-β-1-aξα-β-1)-1＞0.

对于可测函数m:J→R,定义其范数为

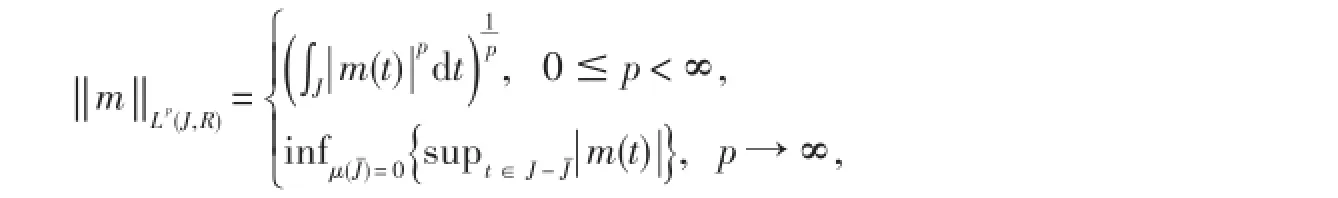
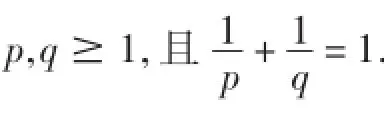
定理2.6（Krasnoselskii不动点定理）设D是Banach空间X的非空闭子集，映射A,B满足：

（ⅰ）当x,y∈D时，Ax+By∈D；

（ⅱ）A是连续且紧的；

（ⅲ）B是一个压缩映射；

则存在z∈D,使得z=Az+Bz.

3 主要结论

定义X=C(J,R),其范数‖u‖=supt∈J|u(t)|,显然X为一个Banach空间.

接下来，我们分别利用压缩映像原理和Krasnoselskii不动点定理给出了边值问题（1）解的存在性和唯一性的两个充分条件.

贯穿全文，给出下列条件：

（H1）f:J×R×R→R是连续的；

（H2）存在q1∈(0,1)和一个非负实值函数,使得对每一个t∈J和所有的u∈X,都有|f(t,u(t),(Au)(t))|≤h(t);

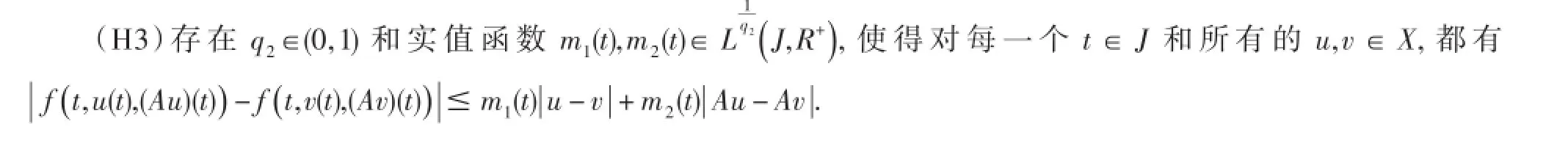
为了方便，引入下列记号

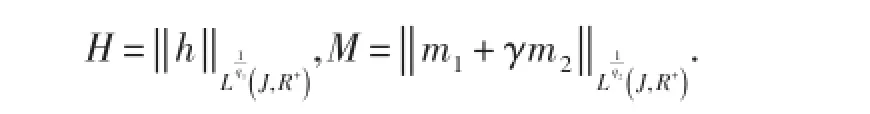
定理3.1假设条件（H1）-（H3）成立，如果

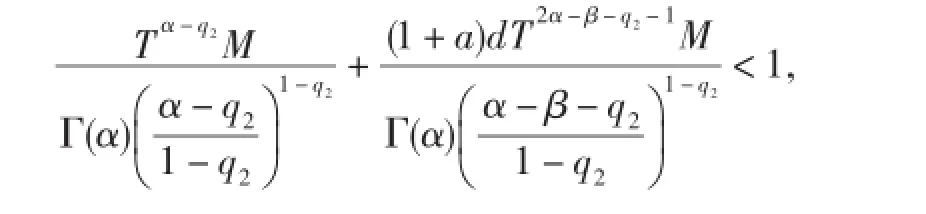
则边值问题（1）有唯一解.

证明由引理2.4可知，边值问题（1）等价于下述积分方程

因此，将边值问题（1）的唯一解等价于映射F在Br上有唯一的不动点.

首先证明F:Br→Br.由条件（H2）和Holder不等式有

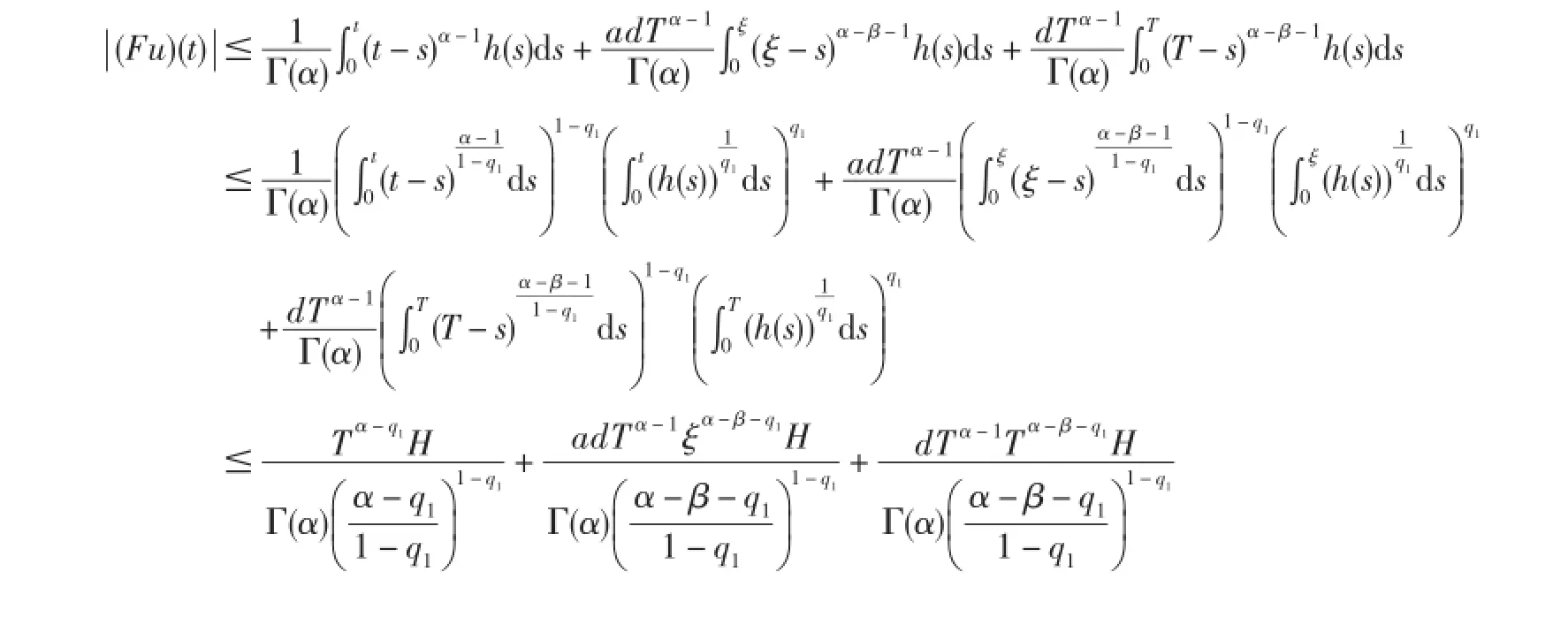
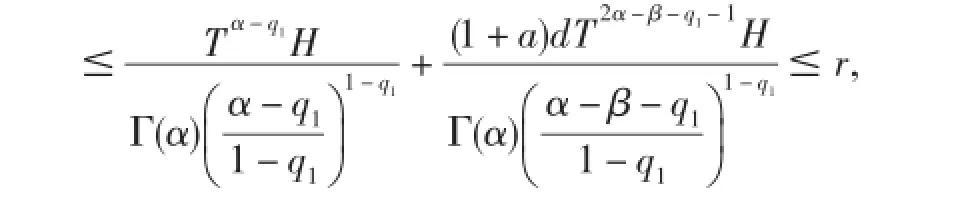
从而有‖Fu‖≤r,即F:Br→Br.

再证，F在Br上是一个压缩映射.对任意的u,v∈X,t∈J，由条件（H3）和Holder不等式有

由Banach压缩映像原理可知，边值问题（1）有唯一解.

定理3.2假设条件（H1）-（H3）成立，如果

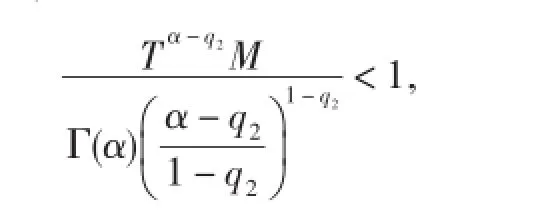
则边值问题（1）至少有一个解.

证明将边值问题（1）转化为不动点问题，在Br上定义映射F如定理3.1中（3）式所示.为了利用Krasnoselskii不动点定理，我们将映射F拆分为F1+F2,其中

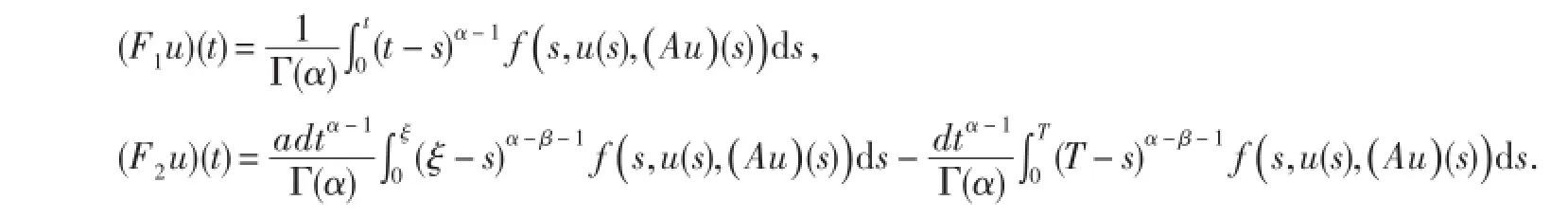
为方便起见，我们将证明过程分为以下几步.

（Ⅰ）对任意u,v∈Br,有F1u+F2v∈Br.

由定理3.1的证明可知因此，F1u+F2v∈Br.

（Ⅱ）F1是一个压缩映射.

显然F1:Br→Br.对任意的u,v∈Br,t∈J,由条件（H3）和Holder不等式有

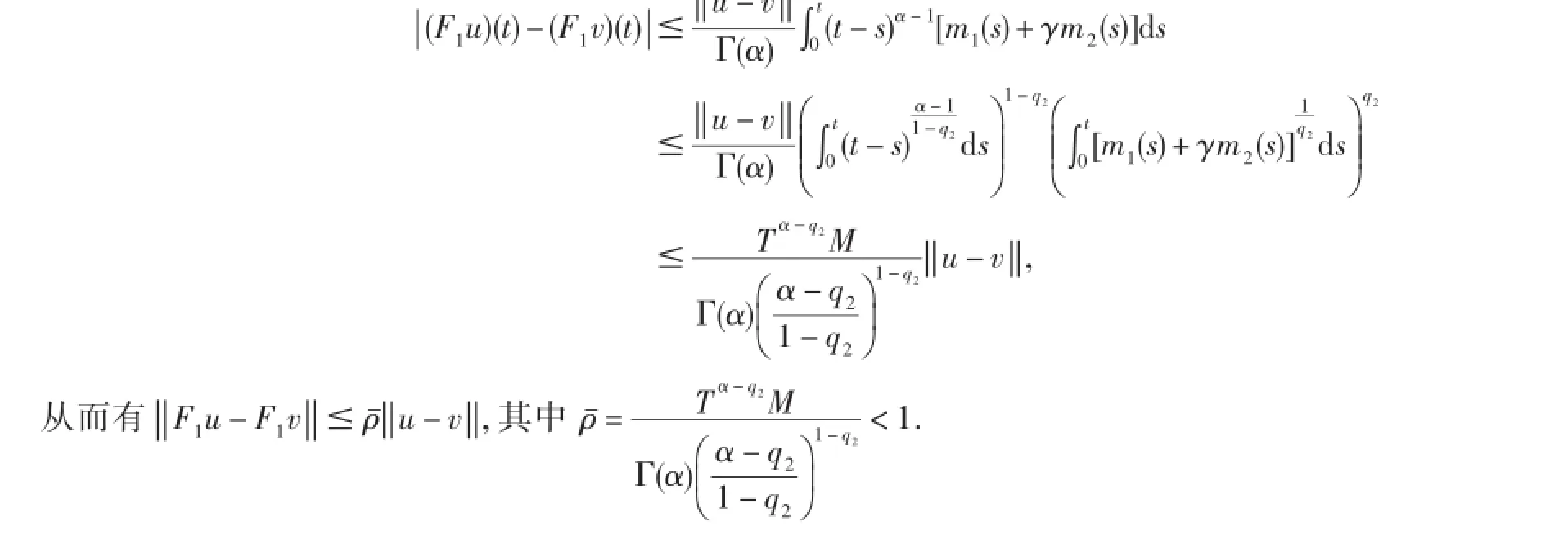
因此，F1是一个压缩映射.

（Ⅲ）要证F2是连续且紧的.

先证F2是连续的.取{un}⊂X,使得un→u.由Lebesgue控制收敛定理，当un→u时，Aun→Au.因此，对每一个t∈J,有

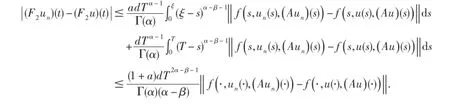
由f的连续性，我们有‖F2un-F2u‖→0,n→∞.

其次，证F2将有界集映成有界集，即证存在μ＞0,使得对每一个u∈Br={y∈X:‖y‖≤r},都有‖F2u‖≤μ.

对每一个t∈J,由（H1）和Holder不等式有

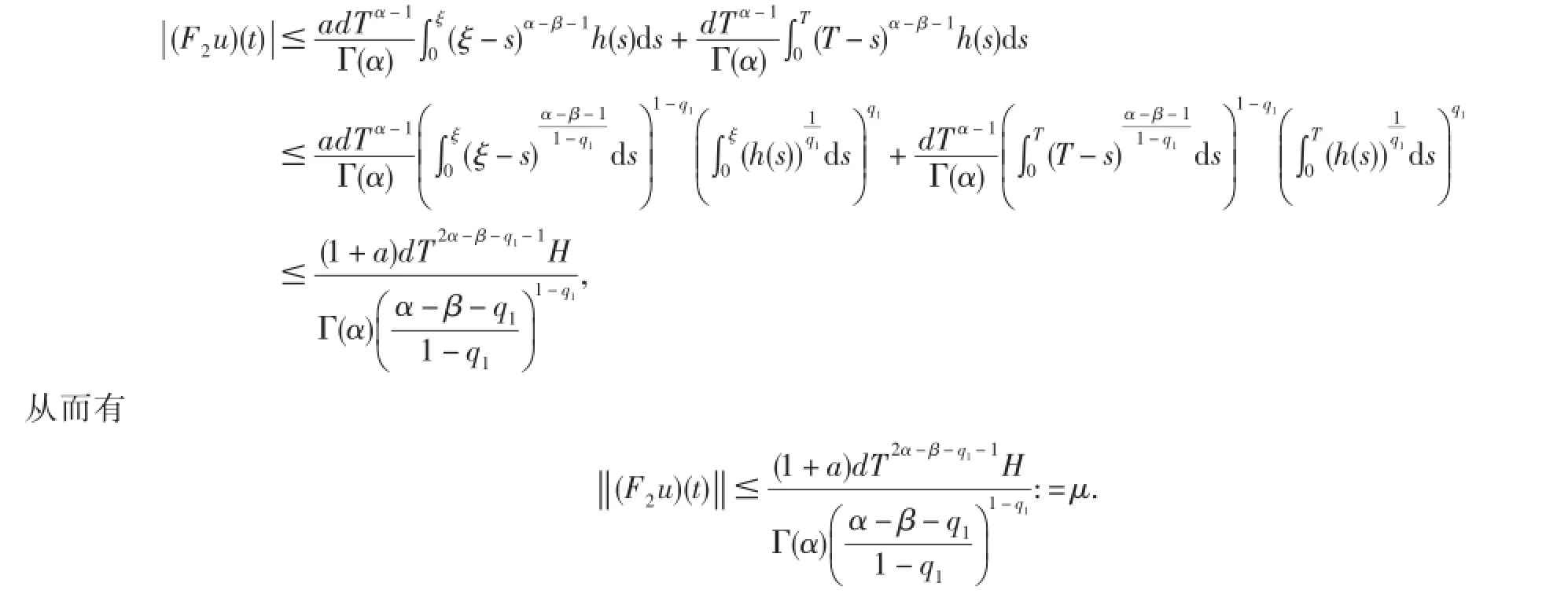
最后，证F2将有界集映成等度连续集.

取0＜t1＜t2＜T,u∈Br,则有

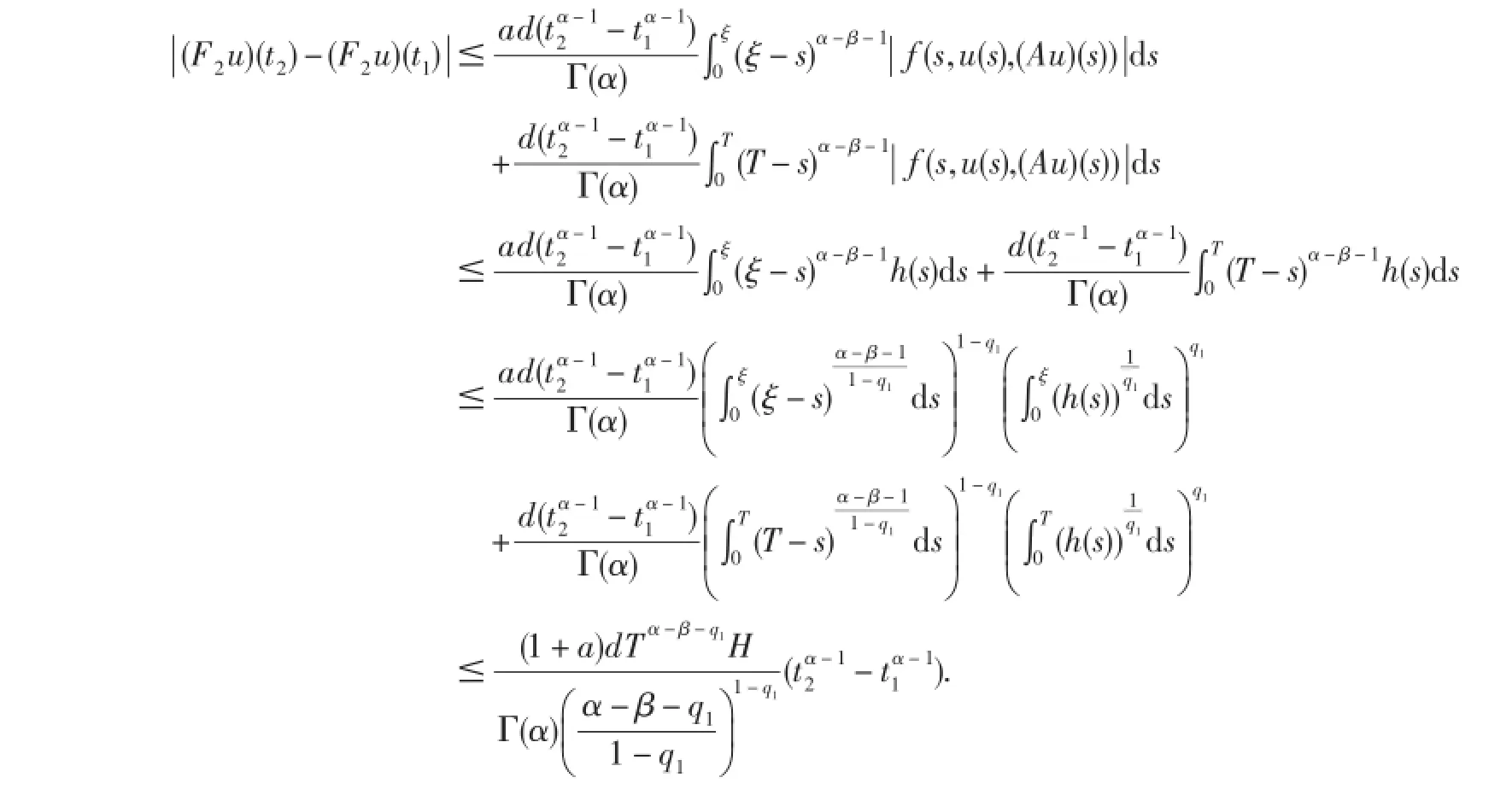
当t2→t1时，有|(F2u)(t2)-(F2u)(t1)|→0,则F2在J上等度连续.

因此，由Arzela-Ascoli定理，F2是连续且紧的.

结合以上证明及Krasnoselskii不动点定理，边值问题（1）至少有一个解.

[1]Kilbas A A,Srivastava H M,Trujillo J J.Theory and Applications of Fractional Differential Equations[M].Amsterdam:Elsevier Science B V,2006.

[2]Podlubny I.Fractional Differential Equations[M].NewYork:Academic Press,1999.

[3]Karthikeyan K,Trujillo J J.Existence and Uniqueness Results for Fractional Integrodifferential Equations with Boundary Value Conditions[J].Communications in Nonlinear Science and Numerical Simulation,2011,doi:10.1016/j.cnsns.2011.11.036.

[4]Karthikeyan P.Some results for boundary value problem of an integro differential equations with fractional order[J].Dynamic Systems and Applications,2011,20:17-24.

[5]Ahmad B,Nieto J J.Existence of solutions for anti-periodic boundary value problems involving fractional differential equations via Leray-Schauder degree theory[J].Topol Methods Nonlinear Anal,2010,35:295-304.

[6]Li C F,Luo X N,Zhou Yong.Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations[J].Comput Math Appl,2010,59:1363-1375.

[7]Bai Z B.On positive solutions of a nonlocal fractional boundaryvalue problem[J].Nonlinear Analysis:Theory,Method＆Applications, 2010,72:916-924.

[8]Ahmad Bashir,Nieto Juan J.Anti-periodic fractional boundary value problems[J].Comput Math Appl,2011,62:1150-1156.

Existence of Solutions for Fractional Integrodifferential Equations with 3-point Boundary Value Problem

ZHU Yan,GU Chang-chao,WU Ting,SUN Lin
(School of Mathematical Sciences,Anhui University,Hefei 230039,China)

In this paper,a study is made of existence and uniqueness of fractional integrodifferential equations with 3-point boundary value conditions by means of Banach contraction principle and Krasnoselskii fixed point theorem.

fractional integrodifferential equations;boundary value problem;existence;uniqueness;fixed point the⁃orem.

O175.8

A

1008-2794（2012）04-0035-06

2012-03-17

高等学校博士学科点专项科研基金联合资助课题“随机泛函微分方程的单调半流理论及应用”（20113401110001）

朱彦（1988—），女，江苏泰州人，安徽大学数学科学学院研究生，研究方向：微分方程．