一类多叶解析函数的性质
2012-04-20徐能朱惠秋
徐能,朱惠秋
(1.常熟理工学院数学与统计学院,江苏常熟 215500;2.常熟市外国语初级中学,江苏常熟 215500)
一类多叶解析函数的性质
徐能1,朱惠秋2
(1.常熟理工学院数学与统计学院,江苏常熟 215500;2.常熟市外国语初级中学,江苏常熟 215500)
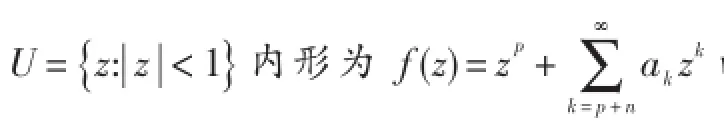
解析函数;p叶函数;星形函数;近于凸函数;从属
1 引言
设f(z),F(z)在单位开圆盘U={z:|z|<1}内解析,我们称函数f(z)在U内从属于F(z)并记作f(z)≺F(z)(z∈U),如果存在U内解析函数w(z)使|w(z)≤|z|且f(z)=F(w(z))(z∈U).又若F(z)在U内单叶,则f(z)≺F(z)(z∈U)当且仅当f(0)=F(0),f(U)⊂F(U).
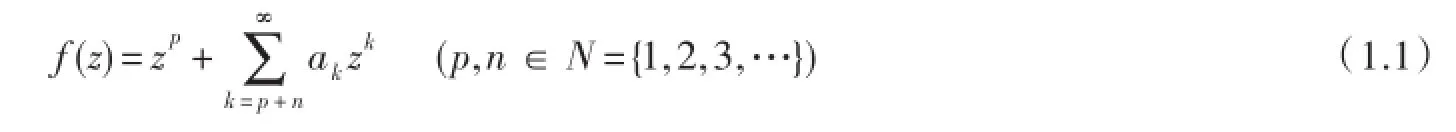
的解析函数类.若f(z)∈Ap,n满足

称f(z)在类kp,n中.熟知kp,n中每一函数是p叶近于凸的.若f(z)∈Ap,n满足

为避免重复,全文设
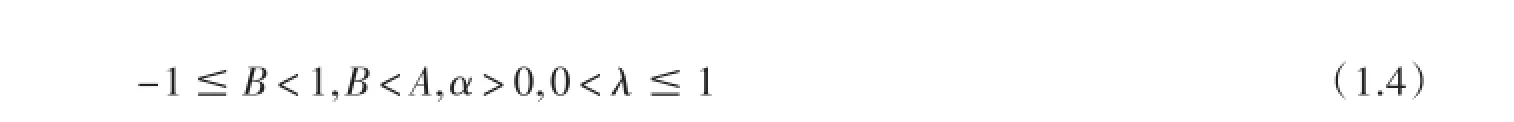
我们引进Ap,n的新子类Hp,n(A,B,α,λ)如下:
定义函数f(z)∈Ap,n称为在类Hp,n(A,B,α,λ)中,若f(z)满足
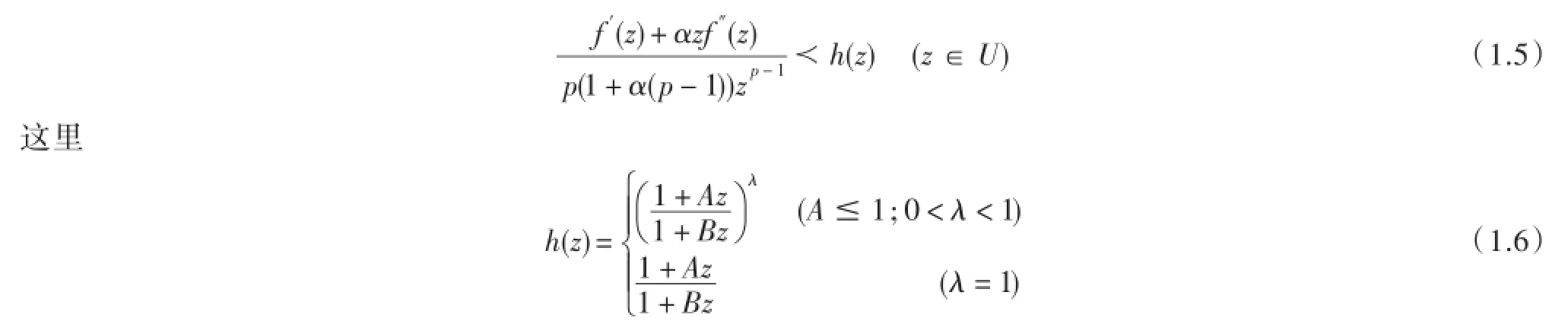
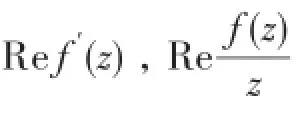
2 一些准确的界
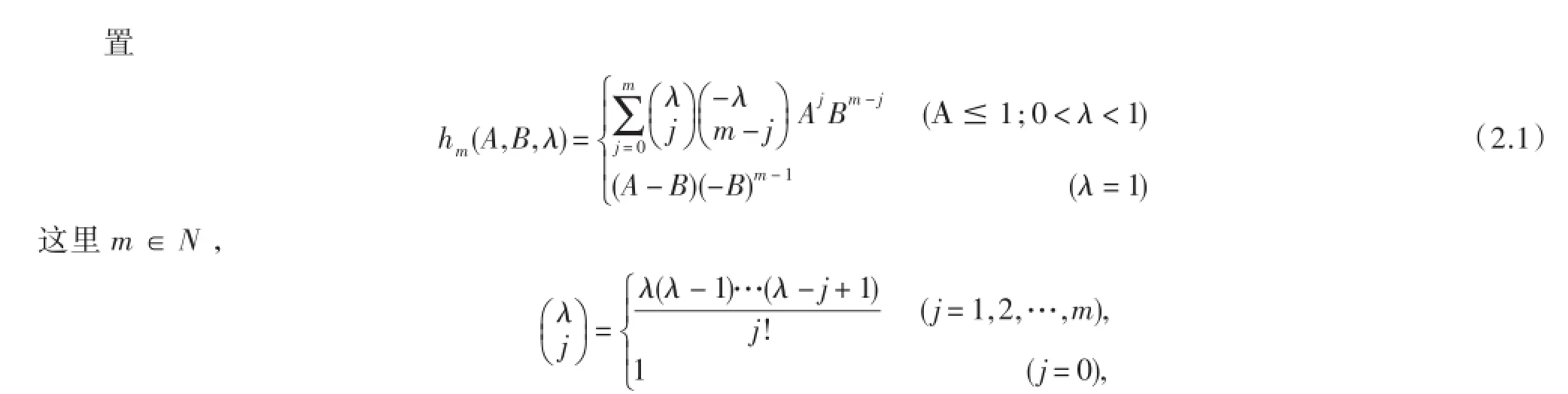
容易知道(1.6)定义的函数h(z)可展开成
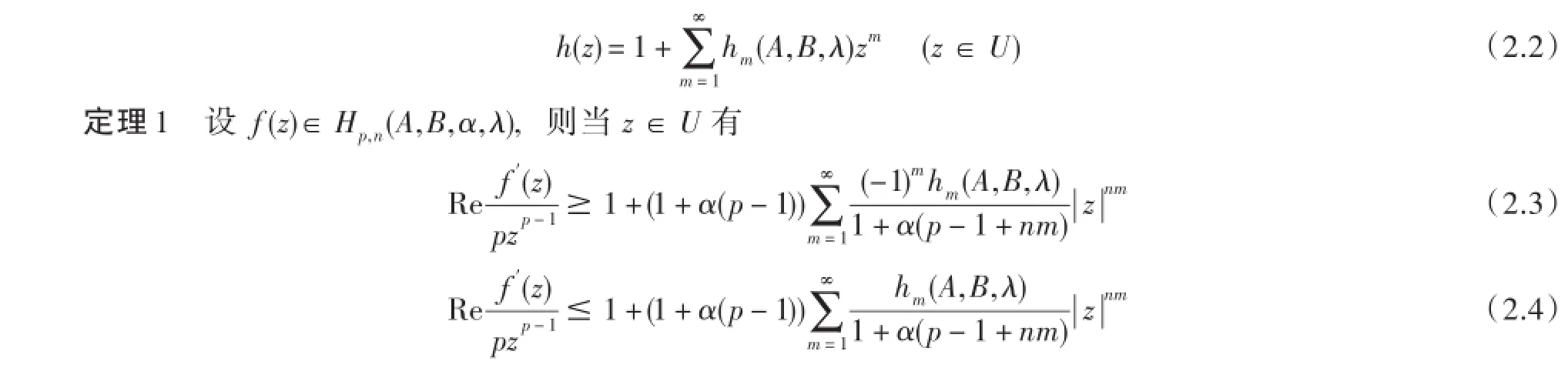
(2.3)和(2.4)中的界皆准确,有极值函数
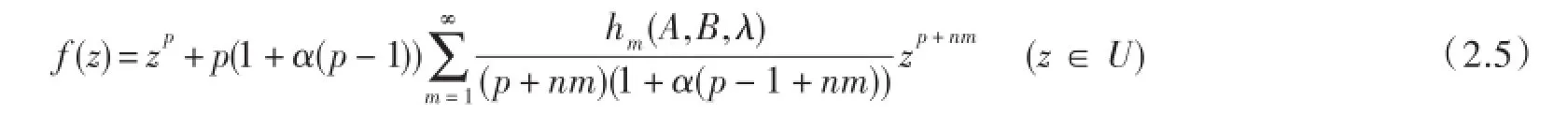
证明由于(1.6)定义的解析函数h(z)在U内凸(单叶)的(见文献[11])且满足h=(z∈U),故当|ξ|≤σ(ξ∈C;σ<1)有

设f(z)∈Hp,n(A,B,α,λ),则按定义可知
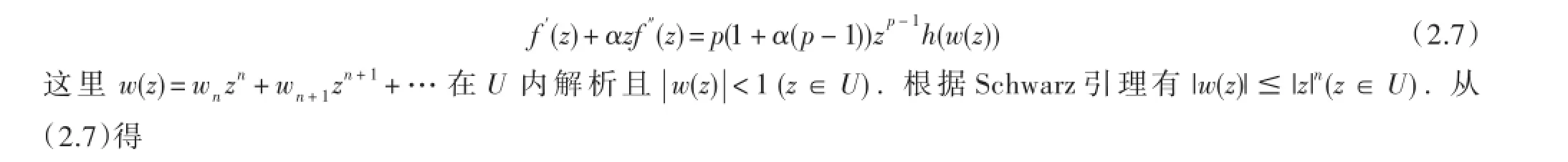

类似地,从(2.2),(2.6)右端不等式与(2.8)可得到(2.4).
对于(2.5)定义的函数f(z),容易验证

结果皆准确.
证明当λ=1,从定理1证明中(2.9)得
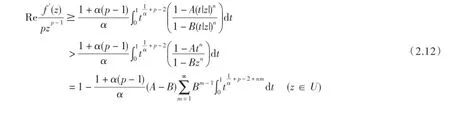
由此立得(2.10).类似的,从
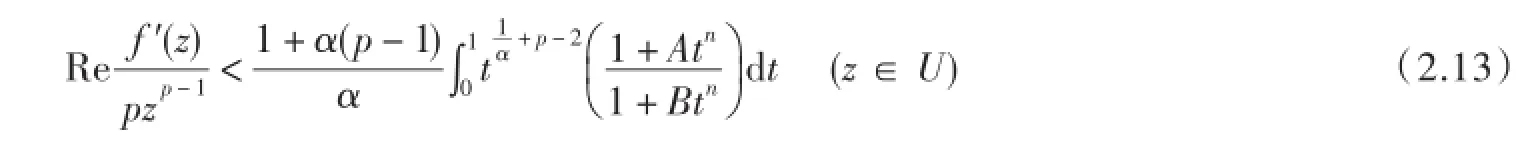
可得(2.11).而且所得估计皆准确,有极值函数
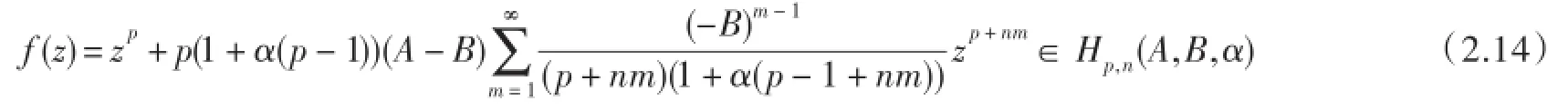
定理2设f(z)∈Hp,n(A,B,α,λ),则当z∈U有
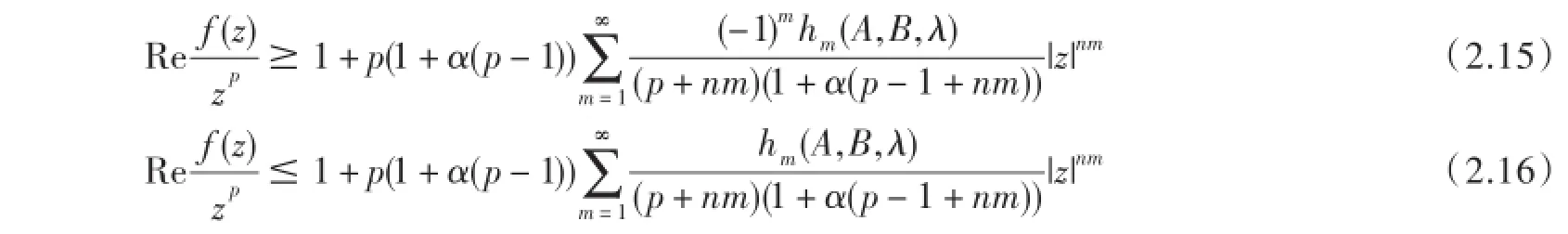
结果皆准确.
证明设f(z)∈Hp,n(A,B,α,λ),因为

利用定理1中(2.3),从(2.17)产生
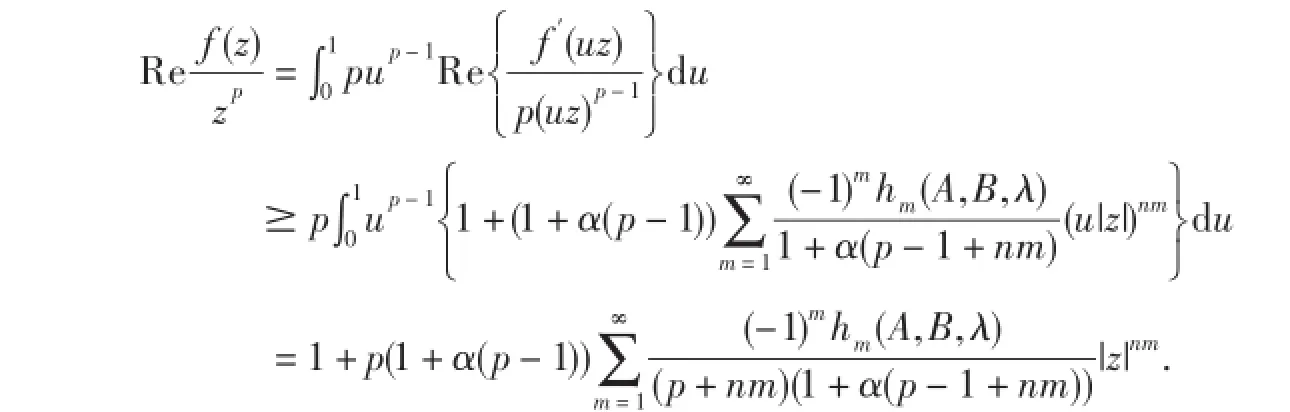
同理,利用定理1中(2.4)与(2.17)可得(2.16).而且,(2.5)定义的函数表明(2.15)和(2.16)是准确的.
推论2设f(z)∈Hp,n(A,B,α,),则当z∈U有

结果皆准确.
证明设f(z)∈Hp,n(A,B,α),则从推论1证明中(2.12)产生
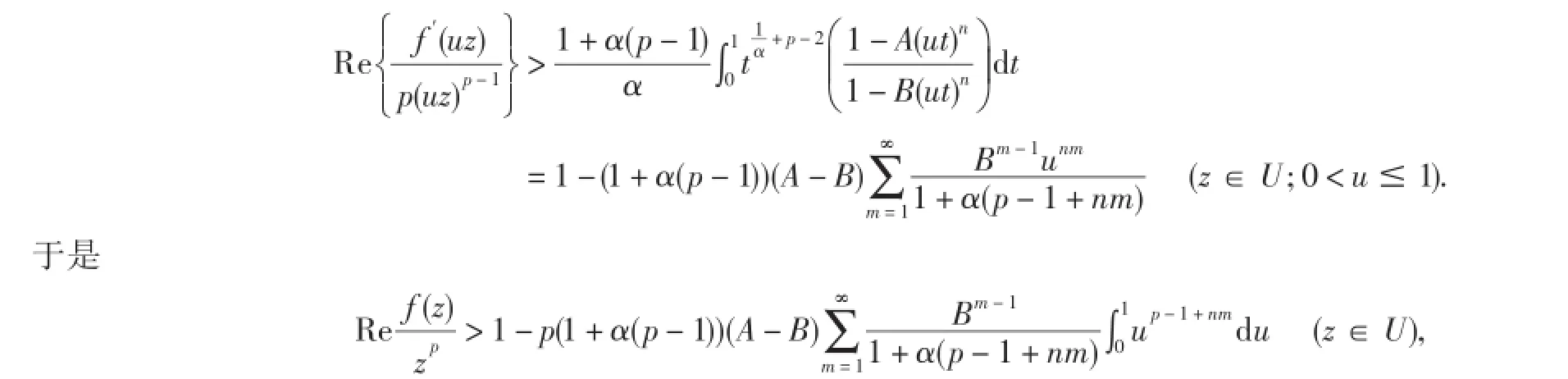
即(2.18)成立,类似地,利用(2.13)和(2.17)可得(2.19).而且,(2.14)给出的函数f(z)表明所得结果(2.18)和(2.19)皆准确.
定理3设f(z)∈Hp,n(A,B,α,λ),AB≤1,则当z∈U有

结果是准确的.
证明已知
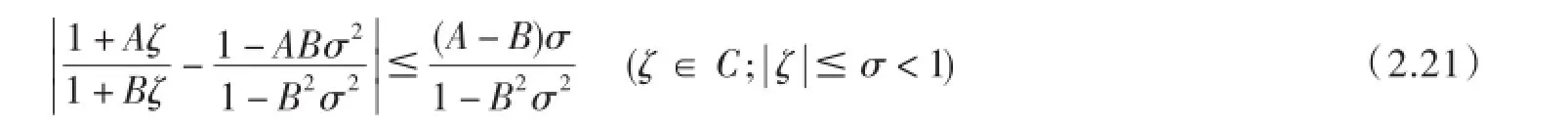
因为AB≤1,有1-ABσ2>0,于是(2.21)产生

现在,对于z∈U与0≤u≤1,从(1.6),(2.2),(2.8)和(2.22)导致
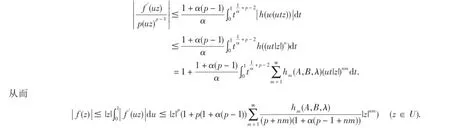
此外,(2.20)中等号被(2.5)定义的函数f(z)在z=|z|到达.定理得证.
引理1[12]若

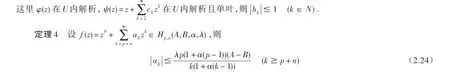
估计(2.24)是准确的.
证明注意h(z)=1+λ(A-B)z+…,函数


此即要证的估计(2.24).
其次,考虑函数
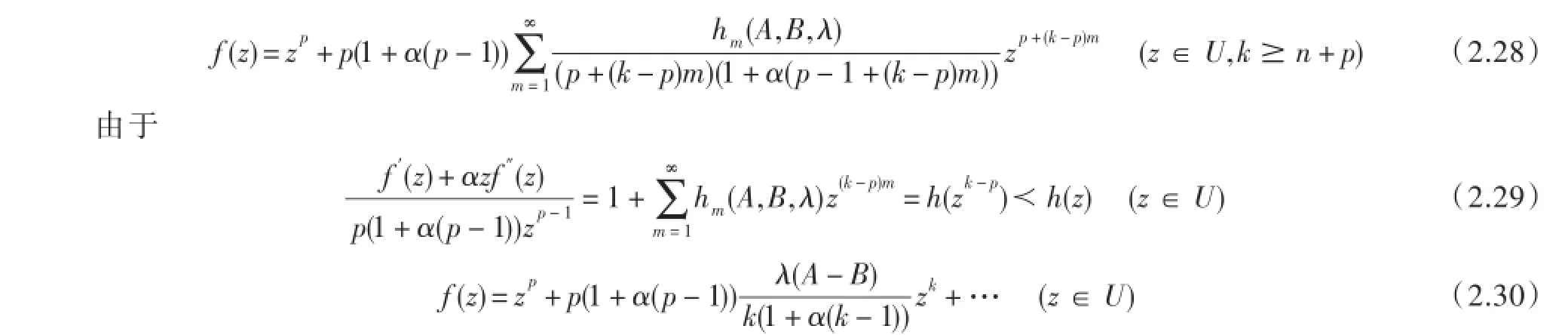
我们看到f(z)∈Hp,n(A,B,α,λ)且系数估计(2.24)是准确的.
3 Hp,n(A,B,λ)的p叶近于凸性与p叶星形性条件
定理5Hp,n(A,B,λ)是kp,n的子类当且仅当
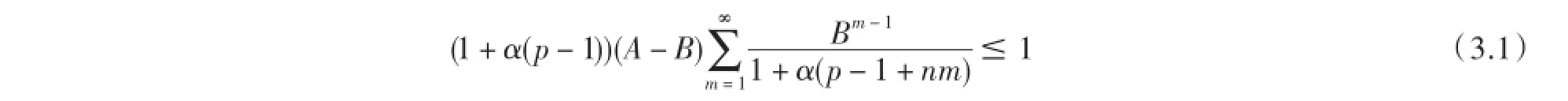
证明设f(z)∈Hp,n(A,B,λ)且条件(3.1)是满足的,则由推论1中(2.10)有
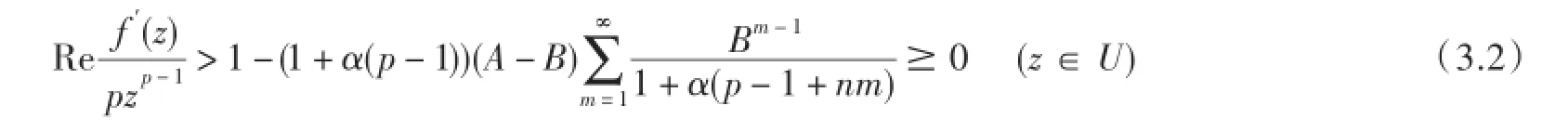
故f(z)∈kp,n.从而Hp,n(A,B,α)⊂kp,n.
另一方面,假设

最后给出Hp,n(A,B,α)⊂的充分条件.为此需要以下结果:
引理2(文献[13],定理4(i))设内解析,g(z)≠a.若0<|z0|<1, Reg(zo)=min|z|≤|z0|Reg(z),则

定理6设

则Hp,n(A,B,α)是的子类.
证明首先注意当B≥0时,不等式(3.7)显然产生不等式(3.8).设f(z)∈Hp,n(A,β,α)则
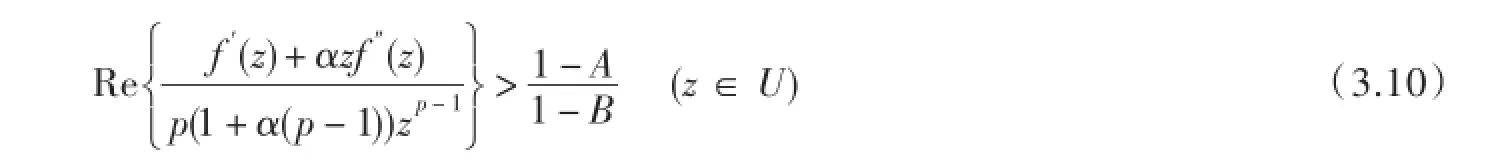
由(3.7)和推论1中(2.10)得
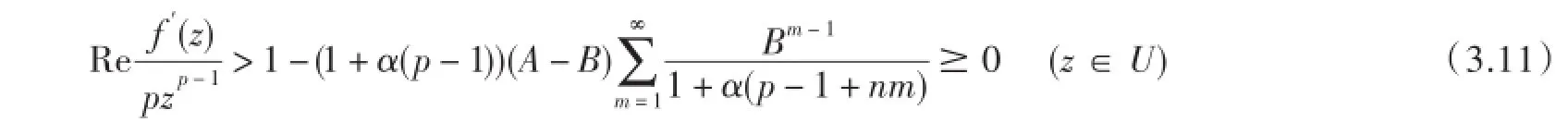
从而(3.8)和推论2中(2.18)产生
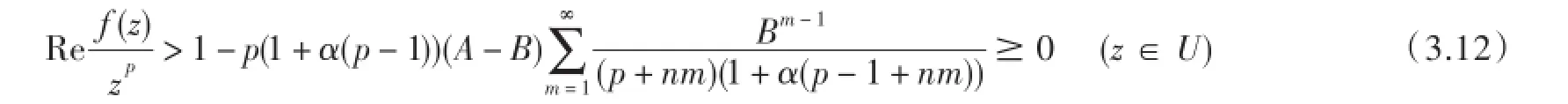
因此,函数
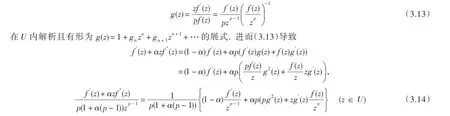
下面要证Reg(z)>0(z∈U).假设存在点zo(0<|zo|<1)使得

则应用引理2有
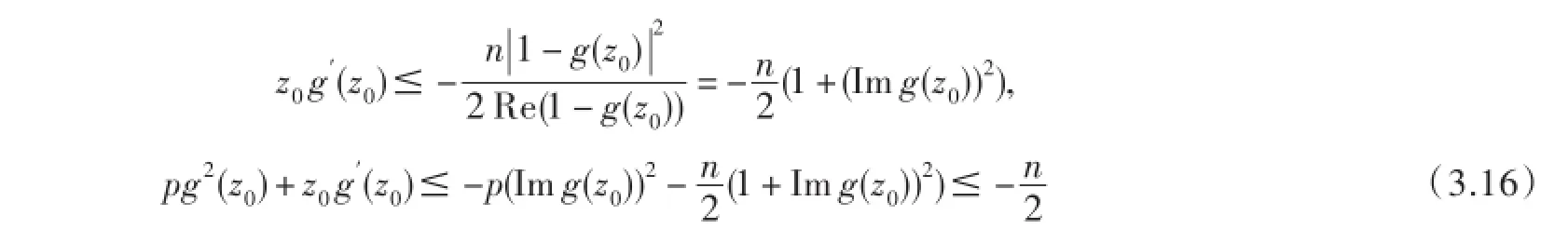
当α≥1,利用(3.9),(3.11),(3.12)和(3.16),从(3.14)推出
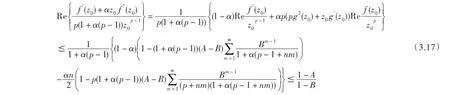
但(3.17)与(3.10)(在z=z0)不相容,从而必有

[1]Chichra P N.New subclasses of the class of close-to-convex functions[J].Proc Amer Math Soc,1977,62:37-43.
[2]Singh R,Singh S.Convolution properties of a class of starlike functions[J].Proc Amer Math Soc,1989,106:145-152.
[3]Ali R M.On a class of starlike functions[J].Rocky Mount J math,1994,24:447-541.
[4]Silverman H.A class of bounded starlike functions[J].Int J Math Math Sci,1994,17:249-252.
[5]Yang D G.Properties of a class of analytic functions[J].Math Japon,1995,41:371-381.
[6]Ponnusamy S,Singh V.Criteria for strongly starlike functions[J].Complex Variables,1997,34:267-291.
[7]Kim Y C,Srivastava H M.Some applications of a differential subordination[J].Int J Math Math Sci,1999,22:649-654.
[8]Kim Y C.Mapping properties of differential inequalities related to univalent functions[J].Appl Math comput,2007,187:272-279.
[9]Yang D G,liu J L.On a class of analytic functions with missing coefficirnts[J].Appl Math Comput,2010,215:3473-3481.
[10]Yang D G,liu J L.A class of analytic functions with missing coefficients[J].Abstract Appl Anal,2011,2011:1-16.
[11]Srivastava H M,Yang D G,Xu N.Some subclasses of meromorphically multivalent functions associated with a linear operator[J]. Appl Math Comput,2008,195:11-23.
[12]Duren P L.Univalent functions[M].New York:Springer-Verlag,1983.
[13]Miller S S,Mocanu P T.Second order differential inequalities in the complex plane[J].J Math anal appl,1987,65:289-305.
Properties of a Class of Multivalent Analytic Functions
XU Neng1,ZHU Hui-qiu2
(1.School of Mathematics and Statistics,Changshu Institute of Technology,Changshu 215500,China; 2.Changshu Foreign Language Junior Middle School,Changshu 215500,China)
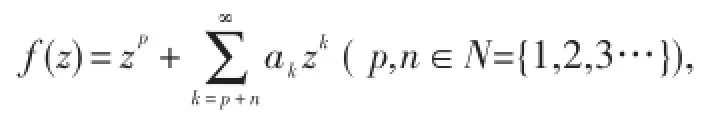
analytic functions;p-valent function;starlike function;close-to-convex function;subordination
0174.51
A
1008-2794(2012)04-0016-08
2012-02-28
国家自然科学基金项目“亚纯函数正规族”子课题(11171045)
徐能(1961—),男,江苏常熟人,教授,研究方向:函数论.
