基于地标信息的星敏感器低频误差标定方法*

熊 凯，汤 亮，刘一武

(1.北京控制工程研究所，北京 100190;2.空间智能控制技术重点实验室，北京 100190)

为了保障对地观测卫星上的有效载荷获取高精度图像，要求卫星姿态确定系统能够准确给出卫星姿态信息.高精度指向卫星广泛采用由星敏感器和陀螺构成的卫星姿态确定系统，即以星敏感器和陀螺作为测量部件，采用卡尔曼滤波(KF)算法并结合卫星姿态运动学方程处理传感器测量信息，实现对卫星姿态误差和陀螺漂移误差的实时估计，修正利用陀螺观测量递推得到的卫星姿态数据，提供星体的三轴姿态信息.

星敏感器是用星光方位来确定卫星姿态的精密姿态测量部件，能够根据多颗恒星矢量的观测数据给出其光轴矢量在惯性系中的坐标.卫星在轨运行过程中受太阳照射角度影响呈现周期性变化，因此自身结构受热不均匀，星敏感器及其安装结构会受其影响而产生形变，导致星敏感器测量输出相对有效载荷基准发生动态偏离.此外，星敏感器观测恒星过程中，其光轴所指向的天区随卫星轨道运动发生周期性变化，导致光学系统误差、标定误差和星表误差随恒星进出视场而发生变化，也会造成周期性误差.星敏感器低频误差指的是在轨卫星上的星敏感器受冷热交变的空间热环境以及视场变化等因素影响而产生的依轨道周期变化的周期性误差，是星敏感器测量误差的重要组成部分，并且很难通过一般的滤波方法消除，是影响卫星姿态确定精度的主要因素之一.通过在轨卫星遥测数据分析认为，星敏感器低频误差可视为周期信号［1-3］;而周期信号看表述为傅立叶级数的形式，即多个正弦和余弦函数的和.国内外针对星敏感器低频误差性能分析、识别和补偿技术的研究可参见文献［4-8］，但基于地标信息的星敏感器低频误差补偿方法在现有文献上尚未见到.

星敏感器低频误差难以利用现有的姿态确定卡尔曼滤波算法予以消除，作为测量误差的星敏感器低频误差会体现在姿态确定结果中，使得姿态确定的精度受到限制.考虑到具有成像能力的卫星有效载荷(如相机或望远镜)具备获取地标方向矢量数据的能力，并且其测量精度较高，可达角秒级，可以作为姿态基准对星敏感器低频误差进行估计和补偿.为了提高卫星姿态确定精度，本文提出，根据有效载荷提供的一个时间序列(几个轨道周期)上的地标方向矢量测量信息，采用批处理的方式，基于最小二乘算法估计星敏感器低频误差参数，即傅立叶级数中各正弦和余弦函数的振幅;进而，根据傅立叶级数形式的低频误差模型和估计得到的低频误差参数，模拟产生低频误差轮廓，并将其用于补偿卫星姿态估计值中星敏感器低频误差的影响.

1 标定方法设计

本节根据有效载荷提供的地标信息，采用最小二乘算法标定星敏感器低频误差.卫星质心到地标的方向矢量在惯性系和星体系的投影分别表示为rI，k和 rB，k，其中，下标 k 表示离散的时间.rI，k可根据卫星和地标之间的位置关系计算得到，rB，k由有效载荷观测得到，二者的关系如下所示:

其中，A(qk)表示由惯性坐标系到卫星本体坐标系的姿态矩阵，可根据卫星姿态四元数qk计算得到，即

其中，

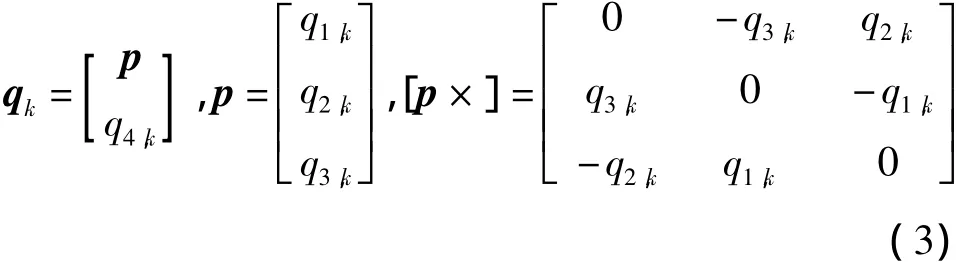
利用扩展卡尔曼滤波(EKF)算法处理陀螺和星敏感器的测量数据，所获得的卫星姿态估计值用来表示，和真实姿态四元数qk的关系可用下式表示

根据四元数乘法定义，

将式(4)代入式(1)可得

令

其分量形式为

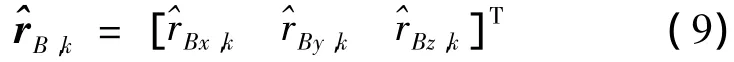
将式(8)代入式(7)得到

考虑到δqk中的各分量为小量，A(δqk)可写为

将式(9)和式(11)代入式(10)可得

或

其中，

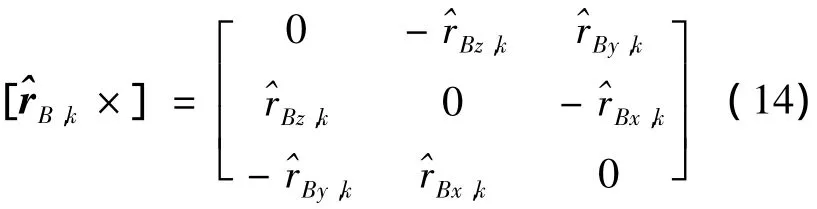
式(13)反映了姿态误差与地标方向矢量的关系，星敏感器低频误差参数辨识可基于式(13)进行.下面需要对低频误差进行参数化.

将受星敏感器低频误差影响的姿态估计误差写为常值项，周期项和随机项之和的形式.

其中，c0=［cx0cy0cz0］T为常值向量，ηk为随机噪声向量，pk表示星敏感器低频误差造成的周期性误差项.将pk写为傅立叶级数的形式，并取其前三阶项

其中，

则式(15)可写为，

或

其中，

将式(18)代入式(13)得到

根据一个时间序列k=1，2，…，N上的有效载荷测量信息构造观测量，

令

由式(19)有

根据式(21)，可通过最小二乘算法获得参数θ的估计值:

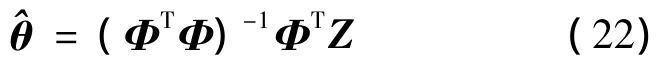
并利用下式实现对卫星姿态数据的修正，

2 实施步骤

为了清楚起见，本节给出基于地标信息的星敏感器低频误差标定流程:

(1)数据获取

通过有效载荷观测若干地标点得到方向矢量rB，k，通过姿态确定EKF算法获得，并根据式(8)计算B，k;通过长时间(几个轨道周期)的观测获得如(20)式所示的用于参数辨识的样本序列Z.

(2)参数辨识

基于样本序列Z，采用如式(22)所示的最小二乘算法辨识低频误差参数 αxj、βxj、αyj、βyj、αzj和βzj(j=1，2，3).

(3)误差补偿

利用式(23)计算星敏感器低频误差造成的卫星定姿误差，采用式(24)补偿低频误差的影响.

(4)有效性检验

实际应用过程中，为了避免增大星上计算机的负担，基于地标信息的星敏感器低频误差参数估计可基于遥测数据在地面执行，获得星敏感器低频误差参数估计值后，再将它们上传到卫星上，形成低频误差的参考轮廓，从而实现对星敏感器低频误差的在轨补偿.

3 数值实例

为了说明本文所述方法的有效性，通过数学仿真对比星敏感器低频误差标定前后的卫星姿态确定精度.

以对地定向的三轴稳定地球同步轨道卫星为例，验证基于地标信息的星敏感器低频误差标定方法的有效性.设陀螺随机漂移为 0.02(°)/h(3σ)，星敏感器测量误差建模为随机噪声和低频误差之和，其中测量噪声方差为5"(3σ)，低频误差的幅度为3".仿真过程中，星敏感器采样周期为1.024s，有效载荷的采样周期为15min，对3个地标点进行观测，3个地标点之间的角距为6°.假定有效载荷的测量误差为3".仿真时间为7天，约7个轨道周期.取滤波周期 τ=1.024s.

先考察星敏感器低频误差补偿前的姿态确定精度.利用现有的卫星姿态确定方法处理陀螺和星敏感器的测量数据，获得的姿态确定结果如图1所示，从图中不难看出，卫星姿态确定误差呈现周期性变化趋势，且变化的周期与轨道周期相同，这显示了星敏感器低频误差对姿态确定精度的影响.

采用基于地标信息的星敏感器低频误差标定方法，对7个轨道周期的卫星姿态估计值和地标观测量进行处理，获得用于补偿星敏感器低频误差影响的参数，并对卫星姿态估计值进行补偿.经过补偿，卫星姿态估计误差如图2所示.与补偿前的结果相比，通过星敏感器低频误差补偿所得到的姿态确定误差显著减小，这说明星敏感器低频误差对姿态确定精度的影响被部分消除了.

表1中给出了星敏感器低频误差补偿前后卫星姿态确定误差的均方根.为了便于对比，表中还给出了体现三轴姿态误差综合影响的精度因子，该精度因子是通过对滚动、俯仰和偏航姿态误差的均方根求平方和得到的.从表中不难看出，星敏感器低频误差的影响经过补偿后，卫星姿态确定精度显著提高.由于地标信息对偏航方向姿态误差形成的几何约束较弱，补偿后星敏感器偏航角误差相对较大.

表1 低频误差补偿前后的卫星姿态确定精度Tab.1 Satellite attitude determination accuracy before and after LFE compensation

仿真结果表明，本文提出的星敏感器低频误差标定方法能够有效消弱星敏感器低频误差的影响，获得优于现有姿态确定方法的精度;低频误差补偿后，卫星定姿误差减小60%.

应当注意，地标点之间的角距减小时，标定的效果有所减弱.尽管如此，当3个地标点之间的角距减小为3°时，采用前述方法进行星敏感器低频误差标定，所得到的三轴姿态估计误差均方根如表1所示，定姿精度仍优于未进行低频误差标定的情况.此外，星敏感器低频误差标定的效果随有效载荷测量精度的降低而减弱.有效载荷的测量误差增大为5"时，三轴姿态估计误差均方根亦如表1所示.

应当指出，以具有高精度成像测量功能的有效载荷作为姿态敏感器，以可精确定位的恒星系统作为绝对参照系，即以恒星代替地标，亦可采用与本文类似方法实现星敏感器低频误差标定.

4 结论

本文提出了基于有效载荷地标观测信息，通过最小二乘算法实现星敏感器低频误差标定的方法，该方法适用于有地标信息的遥感卫星平台.数学仿真结果表明，所提出的星敏感器低频误差标定方法能够显著减小低频误差对姿态确定的影响，改善卫星姿态确定精度.采用该方法有助于提高卫星定姿系统对有效载荷指向的确定精度.在后续工作中，应进一步分析载荷地标预期精度、星敏感器安装方位和卫星轨道误差等因素对低频误差标定精度的影响.

［1］ Jorgensen P S，Jorgensen J L，Denver T，et al.In-flight quality and accuracy of attitude measurements from the CHAMP advanced stellar compass［J］.Acta Astronautica，2005，56:181-186

［2］ Iwata T，Hoshino H，Yoshizawa T，et al.Precision attitude determination for the advanced land observing satellite(ALOS):design，verification，and on-orbit calibration［C］.AIAA Guidance，Navigation and Control Conference and Exhibit，South Carolina，August 2007

［3］ Hashmall J A，Natanson G，Glickman J，et al.Compensation for time-dependent star tracker thermal deformation on the aqua spacecraft［R］.Goddard Space Flight Center，2004

［4］ Blarre L，Ouaknine J，Oddos-Marcel L，et al.High accuracy Sodern star trackers:recent improvements proposed on SED36 and HYDRA star trackers［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Colorado，August 2006

［5］ Schmidt U，Elstner C，Michel K.ASTRO-15 star tracker flight experience and further improvements towards the ASTRO APS star tracker［C］.AIAA Guidance，Navigation and Control Conference and Exhibit，Hawaii，August 2008

［6］ Winkler S，Wiedermann G，Gockel W.High-accuracy on-board attitude estimation for the GMES Sentinel-2 satellite:concept，design，and first results［C］.AIAA Guidance，Navigation and Control Conference and Exhibit，Hawaii，August 2008

［7］ Lam Q，Woodruff C，Ashton S，Martin D.Noise estimation for star tracker calibration and enhanced precision attitude determination［C］.The 5thInternational Conference on Information Fusion，Beltsville，USA，July 2002

［8］ Xiong K，Tang L，Lei Y.Multiple model Kalman filter for attitude determination of precision pointing spacecraft［J］.Acta Astronautica，2011，68:843-852