线阵CCD在风洞轨迹测量试验技术中的应用研究

梁 磊，段丕轩，刘丽萍，王 丹

（中国空气动力研究与发展中心，四川 绵阳 621000）

0 引 言

线阵CCD作为非接触实时空间位移测量的技术手段在国外已经广泛应用。加拿大NDI公司的Optotrak系统精度可达0.1mm，已用于兰利中心、阿姆斯中心的静弹和颤振试验，以及德国／荷兰风洞（DNW）的机翼变形测量和投放试验［1］。国内清华大学和哈尔滨工业大学开展了类似系统的研究，主要应用于医学辅助和姿态测量，精度为0.36mm［2－4］。同线阵CCD测量技术相比，面阵CCD图像数据量大，受数据传输速度的影响，不可能做到高速实时重建坐标，精度也不够高。相对于面阵CCD，线阵CCD的数据量往往要小数千倍，同时线分辨率往往要高数倍，因此线阵CCD在获取模型姿态角、变形量、振动等参数上比面阵CCD具有更多的优势。

国内利用线阵CCD技术进行空间测量还处在研究阶段，笔者介绍了一种利用线阵CCD技术进行空间轨迹测量的方法。

1 系统组成

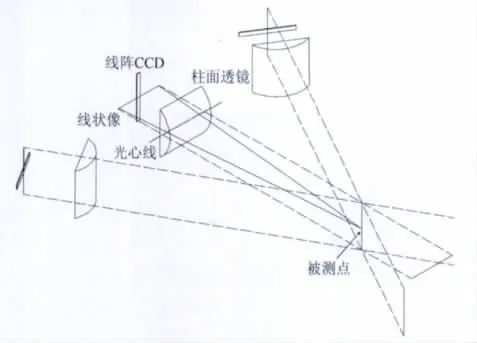
图1 光学系统结构图Fig.1 Schematic of optical system

系统原理见图1，3个一维成像单元组成光学系统，覆盖在同一区域，其中两个相机的柱面镜水平摆放，另外一个相机的柱面镜垂直摆放，能够确定3个相交平面。柱面透镜实现从点到线的光学变换，像点确定一个包含被测点的平面，由3个相交平面得到被测点的位置。一维成像单元中，采用东芝TCD1501D线阵CCD作为图像传感器，和50mm焦距的柱面透镜光心线相互垂直，线阵CCD位于柱面透镜的焦平面上。

如图2，采用7系数直接线性变换（DLT，Direct Linear Transformation）完成相机校准和坐标重建。

研制的基于线阵CCD的实时空间位移测量系统见图3。主要由有源标识、光学系统、采集处理系统、自动标定系统、采集与标定软件组成。线阵CCD测量系统结构框图见图4。

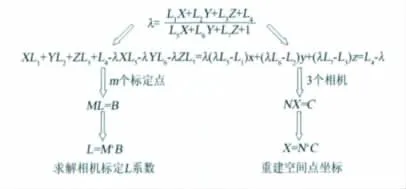
图2 直接线性变换坐标测量过程Fig.2 Measurement process using direct linear transformation

图3 基于线阵CCD的实时空间位移测量系统Fig.3 Real－time spatial displacement measurement system based on linear CCD

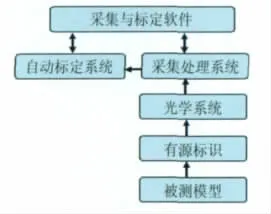
图4 系统结构框图Fig.4 System structure diagram

2 信号处理方法研究

信号处理是技术应用的关键。通过实践研究，提出了一种基于特征边缘提取的组合特征定位WBT算法，对原始信号先进行小波降噪，再使用B样条插值10倍细分，最后取3个阶梯阈值与峰值加权计算，可以有效地提高系统精确度。

2.1 小波变换降噪

Swdldens等人提出了一种完全在时空域构造小波的提升算法（Lifting scheme），5／3提升小波只有一次预测和更新的过程，系数为2的幂次，从追求运算速度和缩小硬件面积的角度看，5／3提升小波更有优势，因此小波变换降噪采用该方法。

提升公式：

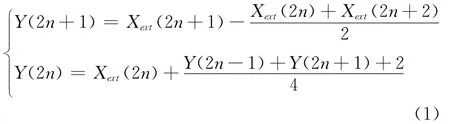
逆变换公式：

其中，X（n）为边界扩展后的输入信号；Y（n）为输出信号。

应用到线阵CCD信号处理中，波形见图5，坐标精度改善结果见表1。

小波降噪后波形进行了一定的平滑处理，虽然在总体来说修正点数不多，但处理之后，对系统精度有明显提高，x轴精确度从0.31mm提高到0.17mm。

表1 小波降噪重建坐标精确度对比Table 1 Accuracy comparison of coordinate reconstruction using wavelet de－noise

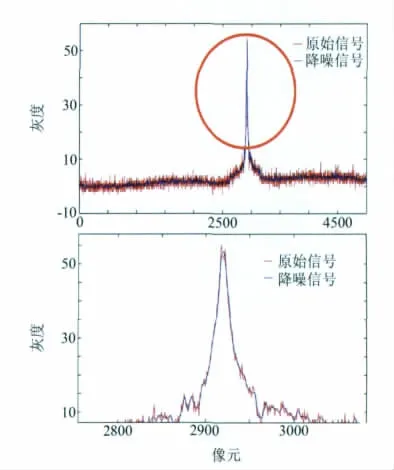
图5 小波降噪波形及局部放大Fig.5 Wavelet de－nolse wavefrom and detail view

2.2 加权阈值峰值定位

对数据深入分析，可知道信号边缘带有更多的信息。峰值也是一种特殊的边缘。单纯计算峰值可能会损失有用的信息。以峰值的0.9，0.8，0.7倍分别作为阶梯阈值，其与波形相截得到的坐标值的1／2，求得一个边缘中心平均值，将该3个值与峰值加权平均，越靠近峰值权值越重。

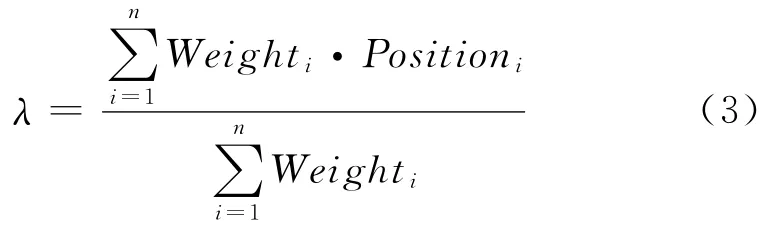
其中，λ为有源标识中心位置；Weighti为第i个阈值的权值；Positioni为第i个阈值截线中心位置；n为阈值的个数，这里取n＝4。

计算结果波形见图6，坐标精度改善结果见表2，系统精度有明显改善。

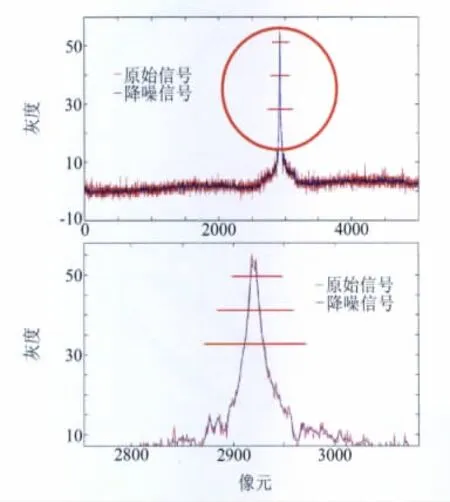
图6 加权阈值峰值定位波形Fig.6 Waveform of weighted threshold and peak positioning

表2 加权阈值峰值定位重建坐标精确度对比Table 2 Accuracy comparison of coordinate reconstruction using weighted threshold and peak positioning

2.3 B样条插值细分

小波降噪后的波形仍然是像素级的，采用加权阈值峰值默认两个像素之间是直线连接。为了得到精度高的亚像素边缘，通过B样条插值对相邻两个像素进行10倍细分，之后再用加权阈值峰值来从边缘值求中心点。

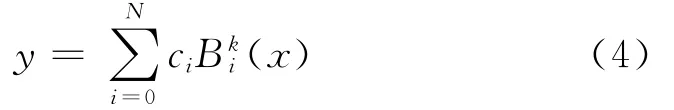
其中，y为对应内节点的坐标值；N为内节点数；ci为控制系数向量（x）为k次B样条基函数。

处理波形见图7，坐标重建精确度对比见表3，可以获得更优化的结果精确度。

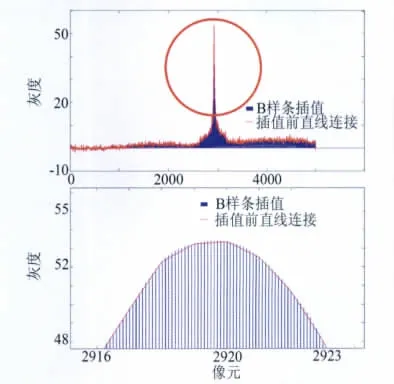
图7 B样条插值细分波形Fig.7 B－spline interpolation subdivision waveform

表3 B样条插值细分重建坐标精确度对比Table 3 Accuracy comparison of coordinate reconstruction using B－spline interpolation subdivision

3 光学系统抗震研究

风洞试验现场洞壁、地板等环境振动很强，造成的相机振动对非接触测量结果有较大影响。采用B＆K3625激振器模拟风洞振动源，对系统分别施加低频单一频率振动和高频随机振动，对振动影响进行研究。

如图8，在3个线阵CCD相机上分别安装B＆K4524－B三轴加速度传感器，在相机测量空间静止点坐标的同时，使用FOCUSII动态信号分析仪采集振动信号。

图8 采集相机振动信号Fig.8 Camera vibration signal acquisition

实验结果如图9，分析试验结果得知，高频随机振动影响了成像质量，使得信号边缘模糊、波形展宽和变形，特征定位难度增加；低频振动对像中心位置影响较大，直接导致坐标重建误差增大。试验表明，采用组合特征定位WBT算法可以有效对抗高频噪声造成的像质模糊、波形展宽和变形，降低了高频随机噪声的影响。

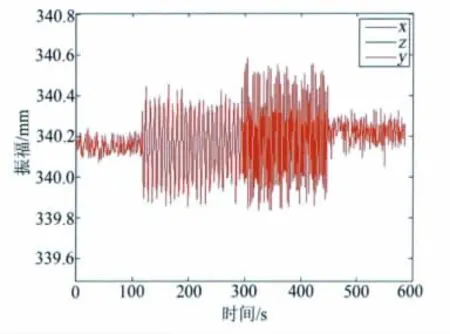
图9 振动模拟试验结果Fig.9 Result of vibration simulation test

采用多周期平均法可以有效提高低频振动时坐标重建的准确性，但对系统的实时性造成一定影响。通过对组合特征定位WBT算法和多周期平均算法的应用，可以使系统的测量精度得到保障。

4 系统应用

由于重大冰雪灾害，致使承担电力运输任务的输电线大量结冰，在覆冰导线空气动力特性和舞动特性的双重作用下，大量输电线扭断，输电塔倒塌，电力系统遭受严重破坏。本研究应用线阵CCD系统测量覆冰输电导线风洞试验中的舞动轨迹。

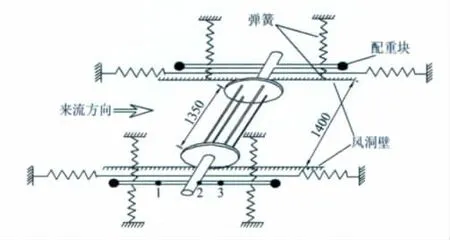
图10 导线舞动试验装置示意图Fig.10 Schematic of conductor galloping locus test device

利用线阵CCD测量系统在1.4m×1.4m风洞测量某型覆冰导线在不同的风速、不同截面形状的覆冰和不同的迎角下的导线群舞动轨迹测量试验。试验装置如图10，试验内容见表4，采集频率为80Hz，结果数据见图11～12，通过试验完成了新月形和扇形覆冰导线舞动规律研究［5］。

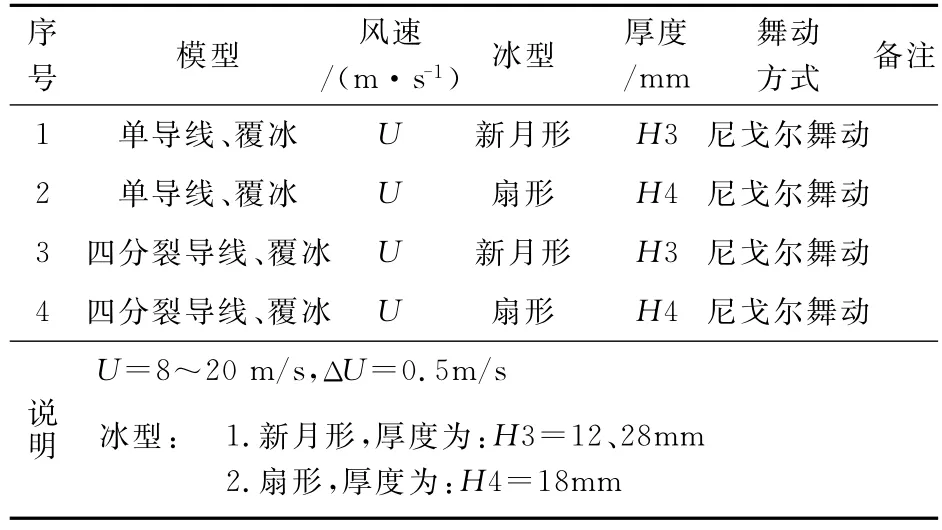
表4 舞动试验内容Table 4 Coment of conductor galloping locus test

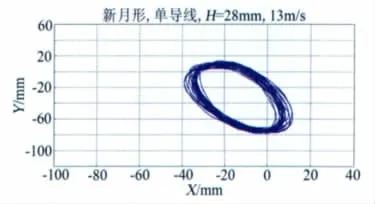
图11 某型覆冰单导线风洞试验轨迹Fig.11 Locus of single－iced－conductor in wind tunnel

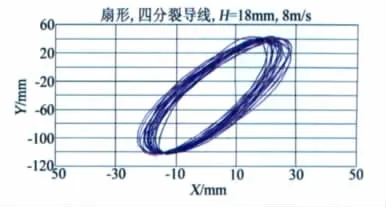
图12 某型覆冰分裂导线风洞试验轨迹Fig.12 Locus of bundle－iced－conductor in wind tunnel

5 结 论

（a）利用线阵CCD对低速风洞模型运动轨迹进行测量，具有实时性好、精度高、灵活方便、性价比高的特点，X、Y轴测量精确度可达到0.14mm，Z轴测量精确度可达到0.60mm；

（b）基于边缘特征提取的组合特征定位 WBT算法，包括小波变换、B样条插值和加权阈值峰值等复合处理技术，较好的抑制了图像噪声和外部高频振动的影响，实现了高精度的亚像素细分定位，定位精度提高54%；

（c）新月形和扇形覆冰单导线发生舞动时运动轨迹均是椭圆形，舞动达到稳定态时，水平位移和竖向位移随时间基本不变。导线舞动时最大双边振幅可达140mm，是导线直径的5倍以上。随着风速的增加，舞动轨迹振幅增大，风速增大到一定程度后舞动将失稳；新月形冰型导线舞动振幅随风速的变化相对明显一些。冰型厚度越大，舞动起始风速越低。参考文献：

［1］ 周述光，温渝昌，金启刚.风洞模型位移光学测量技术应用综述［J］.实验流体力学，2009，23（2）：94－99.

［2］ 吴剑，王广志，丁海曙，等.三维测量系统中线性CCD相机的直接线性变换［J］.清华大学学报（自然科学版），2004，44（6）：860－863.

［3］ 艾莉莉，袁峰，丁振良.应用线阵CCD的空间目标外姿态测量系统［J］.光学精密工程，2008，16（1）：161－165.

［4］ 李晶，袁峰，丁振良.基于BP神经网络的外姿态测量系统线阵CCD标定［J］.仪器仪表学报，2010，31（5）：1138－1141.

［5］ 王丹，黄汉杰.覆冰导线模型1.4米×1.4米风洞试验报告［R］.CARDC报告，2009.