多孔探针系统误差分析

李 鹏，马兴宇，明 晓

（1.南京航空航天大学 自动化学院，南京 210016；2.南京航空航天大学 空气动力学系，南京 210016）

多孔探针系统误差分析

李 鹏1，2，马兴宇2，明 晓2

（1.南京航空航天大学 自动化学院，南京 210016；2.南京航空航天大学 空气动力学系，南京 210016）

以不可压流场的Bernoulli方程和势流理论为出发点详细推导了多孔探针的基本测量原理并获得了相应的数学模型，从而将具有不同头部（如球体、圆锥体）、不同孔数（如3、5、7乃至18孔）的各种类型多孔探针纳入到相同的数学模型之下，为系统分析各类探针提供了条件。通过分析推导过程，得出了多孔探针测量数学模型成立的4个基本约束条件。在实际测量过程中若偏离这4个基本条件必然会在测量结果中引入系统误差。将由此引入的系统误差分别归纳为：数学模型误差、制造误差以及使用误差，并逐个进行了详细的分析。同时，还以较为常用的七孔探针为例，采用计算流体力学软件对以上3种情况造成的误差进行了定量计算。根据以上分析和计算结果，为实际应用中选择合适类型的探针、确定使用条件、评估测量系统误差给出了详细的建议。

多孔探针；系统误差分析；模型误差；制造误差；数值模拟

0 引 言

多孔探针是一种在探针头部分布有若干测压孔的三维流场测试工具，这些探针的头部通常呈球形或圆锥形。根据其头部分布的测压孔数目的不同，多孔探针又可分为三孔探针、五孔探针、七孔探针、九孔探针、甚至十八孔探针。尽管很多基于光电技术的流场测量系统，例如激光多普勒测速仪、PIV系统、热线风速仪等，被广泛使用在三维流场测试领域，但多孔探针作为一种可靠性很高的测试工具仍然具有广阔的应用前景［1－2］，甚至在一些特殊的测试场合具有不可替代性。与光学方法相比，它无需示踪粒子及复杂的光学系统，且对环境震动也不敏感；与热线风速仪相比，其具有较强的抗机械破坏能力。

在多孔探针的使用过程中应对其测量误差的来源和大小做到心中有数，从而帮助提高测量结果的精度，并帮助实验人员判断测量结果的置信区间。尽管不少研究者［3－5］已经用误差分析理论对某一具体类型探针（如七孔或五孔探针）在测量过程中各测量量引入的误差进行了详细分析并给出了其不确定度。但并未从多孔探针基本测量原理的角度系统地研究过其数学模型、制造、使用等方面因素给测量带来的系统误差。本研究将以多孔探针的基本测量原理为出发点深入分析引起多孔探针测量系统误差的多方面原因，并以七孔探针为例运用计算流体力学方法对以上因素进行了定量计算，进而给出相关的系统误差数据。由于采用相同的测量原理及分析方法，因此这些数据可作为其他类型多孔探针使用和分析的参考。

1 测量原理分析

多孔探针测量流场中速度矢量的基本原理是以Bernoulli方程为基础，运用势流理论，通过测量探针头部各孔压力对其绕流的驻点位置及滞止压力进行预测，从而获取待测流场某空间点的速度矢量、总压和静压。

如图1所示，有一头部为球形的探针，并以球心为坐标原点定义直角坐标系，在绕球体的不可压势流场中，若p和u分别为来流的静压和速度，且该流场在球体上的驻点为图中“★”号所示位置，该位置可表示为俯仰角θ和方位角φ，其中θ是速度向量与探头轴线之间的夹角，始终为正。φ是速度向量在YZ平面内的投影与Z平面之间的夹角，迎着探针头部方向看去逆时针为正。pi和ui分别是绕流球体上点i的静压和速度大小。于是对于以上待测量p、u（包括大小u及方向θ、φ），由Bernoulli方程得：

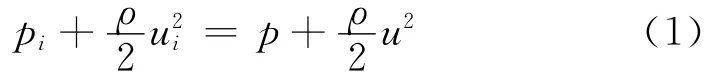
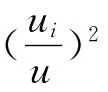
由势流理论可知球体上的速度分布满足如下关系式：

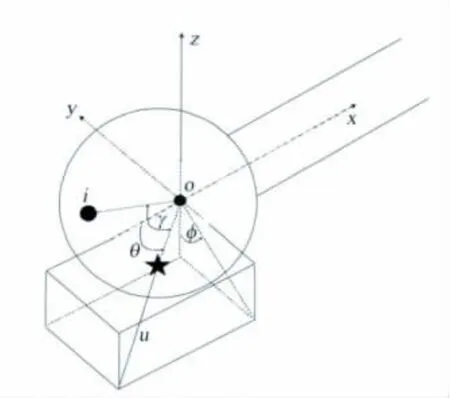
图1 多孔探针测量原理分析示意图Fig.1 The diagram of multi－hole probe measurement principle

其中，γi是驻点与球体上i点对球心连线的夹角，如图1所示。

若孔i在球体上的位置（θi，φi）已知，则可根据简单的几何关系将角度γi表示为驻点位置角θ和φ的函数γi（θ，φ），于是综合式（1）～（3）可得：

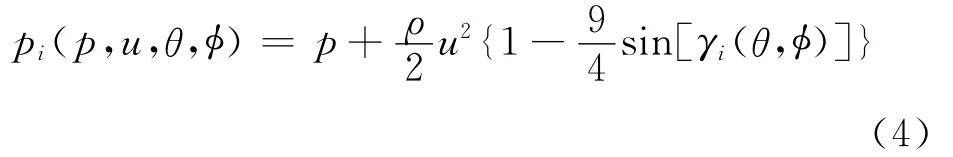
由式（4）可知为了求解4个未知量（p，u，θ，φ），需要至少4个独立的条件使方程封闭，因此探针至少需要4个非共线的测压孔，且这4个测压孔所处区域应与势流理论解接近，例如，这些孔应该避免处于分离区内。这就是为什么运用七孔探针进行大角度测量时只能采用其中4个孔的压力数据进行计算，而在小流动角下可使用7个孔的压力数据进行计算。

由以上分析可知，为了使用探针进行流场速度矢量测量，需要满足如下条件：（1）所使用测压孔实际压力值应与势流理论给出的结果一致；（2）探针头部测压孔的几何位置应与计算模型保持一致；（3）探针测量的应是没有速度梯度的均匀来流；（4）应确保被测流场介质的不可压属性，且测量结果与Reynolds数无关。若实际测量中存在与以上条件偏离的情况，则必然会使测量结果与待测量的真值间存在误差。该误差与文献［3－5］中的误差分析之间的根本区别在于：文献中的误差是由测量压力传感器及数据采集系统引入的，而本文所指误差是由于各种原因使探针系统本身偏离其设计模型而引入的探针系统误差。正如前所述，导致这一系统误差的根本原因就在于实际测量条件与理论设计模型间在以上4个约束条件上的偏离；综合以上4种偏离现象可将引起多孔探针系统误差的原因归纳为多孔探针的模型、制造、使用3方面因素，以下将分别予以分析和讨论。

2 模型误差

由第1节的分析可知，多孔探针测量流场速度矢量的基本方程由式（4）给出，而获得该式的重要依据之一是由势流理论推导出的球体上速度分布规律，即式（3）；由于势流理论并未考虑流体粘性的影响，因此该结果与实际流动必然存在偏差。若将流体粘性影响考虑在内［6］，式（3）可修正为：

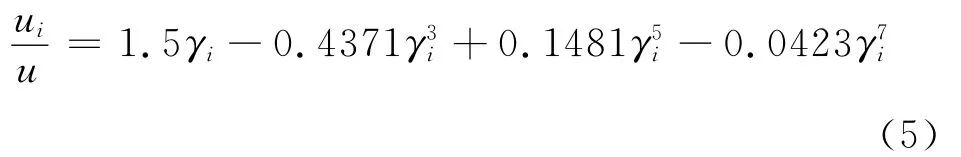
为了便于比较，将式（3）中的正弦函数展开为γi的幂级数形式并重新整理如下：

对比式（5）和式（6）可得到如下结论：

（1）势流理论获得的结果与实际流动存在偏差，该偏差必然会在探针测量结果中引入误差，这种误差是由于对测量探针进行建模时引入的系统误差，即模型误差；（2）以上模型误差随着γi的减小而减小，当γi较小时由模型误差引入的测量偏差可以接受。因此为了提高探针的测量精度，应使测量时获得的γi值尽量小。为达到该目的，应尽可能增加探针头部测压孔的密度。因此为了得到高精度的测量结果，从最基本的5孔、7孔到9孔、13孔甚至18孔的高密度压力孔多孔探针不断出现。

为了定量分析采用势流模型对多孔探针引入的系统误差，接下来将运用计算流体力学软件Fluent进行流场计算。由于制造的原因，目前很大一部分探针采用如图2所示的锥型头部七孔探针［1－5］，因此为了便于对比且为实际使用提供参考，以下数值模拟将以该类型探针为对象进行计算。需要说明的是，锥形头部的探针与球形头部探针的测量原理及模型是一致的；但根据Schlichting［7］给出的数据可知，在表面压力分布上锥型头部探针与球形头部探针相比其实际值与势流理论计算值偏差要大，从而其引入的模型误差必然大于球形头部的探针。图3为用三维网格生成软件Gambit构造的探针表面网格分布。Fluent解算参数如下：流动为低速定常不可压粘性流，控制方程为雷诺平均N－S方程，湍流模型为S－A模型，流场计算区域边界条件为：前方及上方边界处设为速度入流边界，取无穷远来流速度；后方取为压强出流边界；探针表面及孔内表面取为壁面边界条件。无穷远来流速度大小为17m／s，温度为15℃。为了实现测量计算，首先按照相关文献［3］的方法对多孔探针进行了数值校准，以获得校准矩阵。校准计算时，θ角为6°～72°，以6°为间隔；φ角为－25°～325°，以10°为间隔（对于内区，θ和φ将折算为α和β，其中α为迎角，即速度向量在XZ平面内的投影与X轴之间的夹角；β为侧滑角，即速度向量与XZ平面之间的夹角），总计432个状态。考虑到1～6孔具有对称的位置，故只需考虑半区内的3个φ角（如155°、165°和175°），共计36个状态，即可得到各区的校准系数。

具体计算获得的七孔探针各区测量拟合标准偏差，如表1所示。对比文献［8］，数值计算结果与文献实际测量获得的结果较为一致，因此该结果应该是可信的。由于数值计算中不存在压力传感器、数据采集设备、七孔探针制造等因素引入的误差，因此其标准差小于测量结果。但其误差也不能忽视，而该误差应主要来源于本节指出的模型误差。

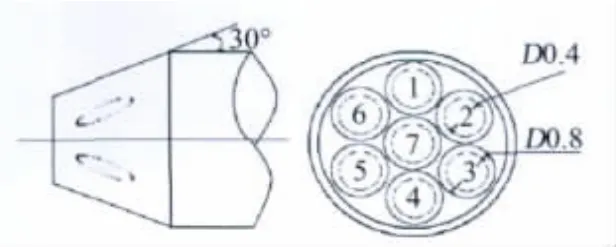
图2 七孔探针几何外形Fig.2 The geometric shape of seven－hole probe

图3 七孔探针的表面网格Fig.3 The surface mesh of seven－hole probe

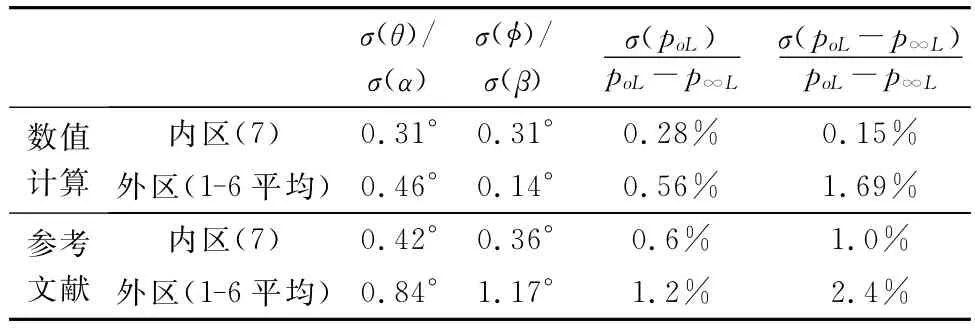
表1 数值标定精度Table 1 Numerical calibration precision

3 制造误差

在第1节的分析中，假定多孔探针上孔i在球体上的位置（θi，φi）已知，从而得到了如式（4）给出探针测量基本模型，但在探针的实际制造过程中由于机械加工的精度限制，探针上各孔的具体位置与设计时给定的模型位置必然存在偏差。为了降低由于这种制造因素带来的影响，实际使用过程中每根探针必须要进行单独校准。然而，这并不能完全消除由此引起的误差。本节将以上节的内容为基础分别对锥形头部七孔探针的4号孔沿径向存在10μm及50μm偏移情况下的标准误差进行计算分析。采用与上一节相同的计算参数并重新调整4号孔的位置及相应网格。因只考虑4号孔径向偏移，2号孔和6号孔、3号孔和5号孔具有对称的位置，故校准时只需计算216个状态。具体计算结果如表2和3所示。

通过表2和3的数据可知：4号孔沿径向外移10μm，对4区的标准偏差影响不大，但对相邻的3区和5区、相对的1区以及7区产生了较大的影响（考虑到偏移量很小）。原因在于4号孔的偏移造成的不对称将通过式（3）给3区和5区的校准引入误差，使得标准偏差增大；1区的σ（φ）显著增大，但σ（θ）及总压和动压的标准偏差反而有了下降，结合表3中偏移50μm的结果可以看出，单纯的4号孔径向外移，使得1区的校准精度（φ除外）略有提高，但随着偏移量的增大，这种效应又会逐渐消失；对于7区，动压的标准偏差有所增大，但σ（α）和σ（β）却有所减小，原因在于4号孔的外移使得式（3）中的3对孔的压力差值增大，对角度的校准精度相应地有所提高。当4号孔沿径向外移50μm时，虽然对1区的标准偏差影响不太大，但4区的标准偏差发生了较大改变，动压的标准偏差已超出2%。因此，综合来说，由于制造误差的存在增大了多孔探针的系统误差，且制造误差越大所带来的系统误差也越大。此外，需要说明的是，由于制造的原因探针头部的光洁度对流动也会产生影响，从而引入误差；但考虑到加工中较容易保证表面光洁度，因此对于这一情况本节中予以忽略。

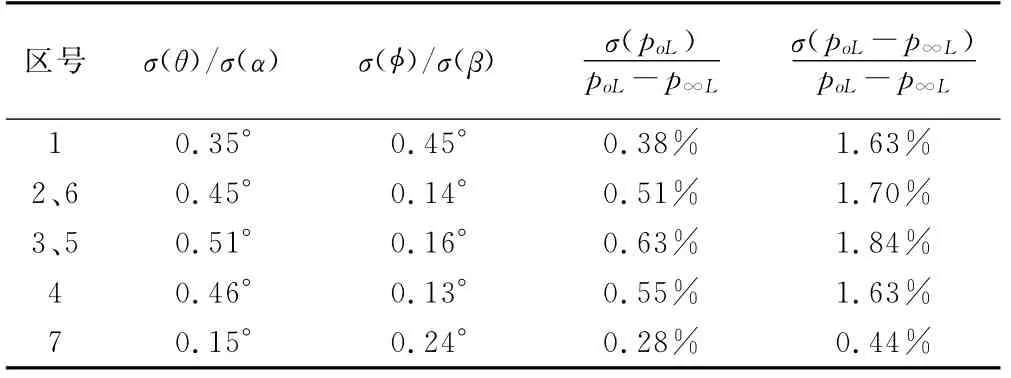
表2 4号孔偏移10μm时校准公式的标准偏差Table 2 The standard deviation of 4hole offset 10μm

表3 4号孔偏移50μm时校准公式的标准偏差Table 3 The standard deviation of 4hole offset 50μm

4 使用误差

4.1 使用速度范围

为了将多孔探针的测量数学模型运用到不同流体介质中测量不同速度，必须要使测量结果独立于流场的Reynolds数。考虑到采用多孔探针测量流场是通过探针头部的压力值导出，因此为了获得独立于Reynolds数的测量结果，可通过考察探针头部的压力分布与Reynolds数间的关系得出一些有益的结论。由于流场中物体的阻力系数CD与其表面的压力分布密切相关，且其与Reynolds数间的关系有丰富的实验数据可以利用，因此要确立与Reynolds数无关的测量结果，可通过考察阻力系数与Reynolds数间的关系获得。由量纲分析可知，阻力系数CD是Reynolds数、马赫数及物体表面粗糙系数¯k的函数。考虑到加工中较容易保证表面光洁度，因此对于物体表面粗糙系数的影响予以忽略。由文献［7］可知：对于光滑球体，在1×103＜Re＜1.8×105范围内，阻力系数CD与Reynolds数的变化几乎无关。于是由此可得到多孔探针使用的速度下限为：

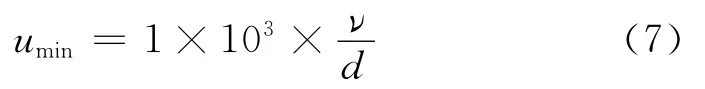
若在20℃下使用直径d＝3mm的探针测量空气（ν≈15×10－6m2／s）的速度，则其最小测量速度应不小于5m／s，否则将会产生较大误差。

此外，由文献［7］知，当马赫数小于0.3时阻力系数CD与马赫数无关，于是可得到多孔探针使用的速度上限为：

其中a为音速。若在20℃下使用多孔探针测量空气（a＝344m／s）的速度，则其最大测量速度应不大于100m／s，否则将会产生较大误差。

4.2 速度梯度误差

以上多孔探针的测量原理是基于速度梯度无关的均匀流场的假设推导的，若实际使用过程中偏离这一假设，如图4所示，当探针处于流线间具有梯度的流场（即剪切流场）中时，也必将给测量带来误差。文献［4］针对五孔探针在速度梯度场中的使用误差做了讨论。利用数值模拟的方法，定量分析速度梯度和探针直径对于测量的影响。这里定义速度梯度k，单位为（m／s）／mm，探针直径d，单位为mm。仍采用第2节中使用的网格及获得的校准矩阵；速度梯度k＝0.1～1.0，增量为0.1；探针直径d＝1～6mm，增量为1mm。

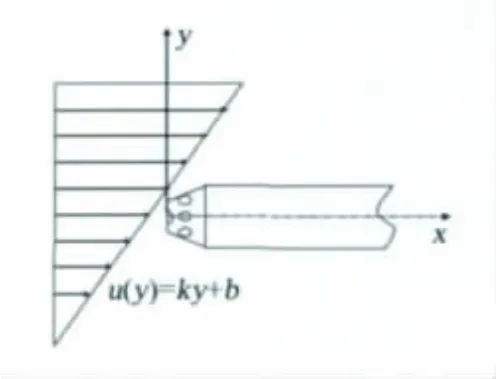
图4 七孔探针测量剪切流场示意图Fig.4 The diagram of measurement shear flow field using seven－hole probe

图5给出了七孔探针测量具有速度梯度的流场时随速度梯度和探针直径变化的角度误差包线。计算结果表明，随着探针直径和待测流场速度梯度的增大，所测量的系统误差也会随之增大，进而导致探针测量的空间分辨率下降。此外，若能将探针尺寸及待测流场速度梯度控制在一个合理的范围内，其相应的误差还是可以接受的。

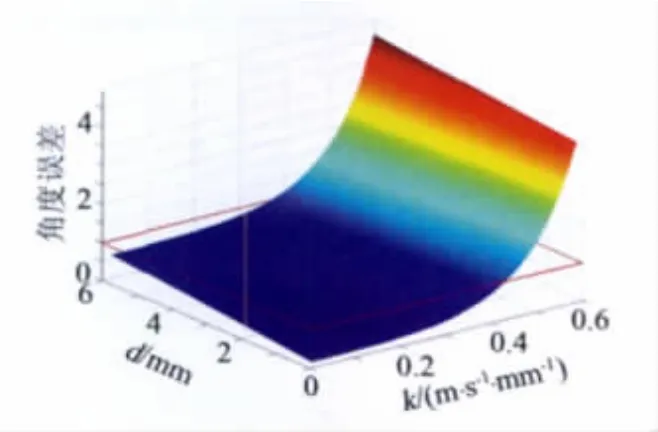
图5 七孔探针测量具有速度梯度流场的误差包线Fig.5 The error line of velocity gradient fluid field using seven－hole probe

5 结 论

以不可压流场的Bernoulli方程和势流理论为出发点详细推导了多孔探针的基本测量原理并获得了相应的数学模型，通过分析推导过程得出了该测量数学模型成立的4个基本约束条件。在实际测量过程中若偏离这4个基本条件必然会在测量结果中引入系统误差。将由此引入的系统误差分别归纳为：模型误差、制造误差以及使用误差，并逐个进行了详细的分析。根据文中的分析，不同类型的多孔探针具有相同的测量原理及分析方法，因此，以较为常用的多孔探针——七孔探针为例，采用计算流体力学软件对以上3种情况造成的误差进行了定量计算。通过这些分析和计算结果可为实际应用中选择合适类型的多孔探针、确定使用条件、评估测量系统误差提供有益的帮助。具体结论如下：

（1）探针选择：通过增加探针头部测压孔的分布密度，即探针孔数，可减小孔间的夹角使得在驻点附近测得的各孔压力值与势流理论的计算结果尽量接近；因此，为了减小系统误差提高测量精度应在可能的条件下选择孔数多的多孔探针；

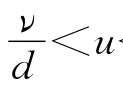
（3）误差变化趋势：由于作为探针测量数学模型建立基础的势流理论与实际流动的偏离必然会给测量带来误差，该误差将随着探针头部测压孔的分布密度、制造定位精度的降低而增大；也会随着测量过程中存在的速度梯度的增加而增加，但由此引起的测量系统误差可通过合理选择探针头部尺寸及测量环境速度梯度上限的方法将其控制在可接受的误差范围内。

［1］PAYNE F M，NG T T，NELSON R C.Seven－hole probe measurement of leading edge vortex flows［J］.Experiments in Fluids，1989，7：1－8.

［2］SUMMER D，HESELTINE J L，DANSEREAU O J P.Wake structure of a finite circular cylinder of small aspect retio［J］.Experiments in Fluids，2004：720－730.

［3］ZILLIAC G G.Modeling，calibration，and error analysis of seven－hole pressure probes［J］.Experiments in Fluids，1993，14：104－120.

［4］GLAHN A，HALLMANN M，et al.Advanced pneumatic method for gradient flow analysis［J］.Experiments in Fluids，1993，15：219－226.

［5］VENKATESWARA BABU C，GOVARDHAN M，SITARAM N.A method of calibration of a seven－hole pressure probe for measuring highly three－dimensional fows［J］.Meas.Sci.Technol.，1998，9：468－476.

［6］WHITE F M.“Laminar boundary layers”in viscous fluid flow［M］.2nd ed.，New York：McGraw－Hill，1991：298.

［7］SCHLICHTING H著.边界层理论［M］.徐燕侯，徐立功等译.北京：科学出版社，1988：10－24.

［8］GERNER A A，MAURER C L.Calibration of sevenhole probes suitable for high angles in subsonic compressible flows［J］.AIAA J，1982，82：404－410.

李 鹏（1977－），男，广西桂林人，讲师，博士生。研究方向：实验流体力学，流动测量。通讯地址：江苏省南京市白下区御道街29号自动化学院测试工程系（210016），联系电话：025－84893451，E－mail：nuaalp＠163.com

System error analysis on multi－hole probe

LI Peng1，2，MA Xing－yu2，MING Xiao2
（1.College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China；2.Department of Aerodynamics，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

Based on Bernoulli equation and potential theory，the mathematical model of multihole probe is derived，which is suitable for multi－hole probe with various shape probe head（such as spherical or conical）and hole number（such as 3，5，7，even 18 ）.Four constraint conditions which ensure that the measurement model is valid are obtained.As an inevitable result of the deviation above constraint conditions the system error is brought to the measurement data.In this paper，the system error is analyzed in detail and summed up as mathematical model error，manufacturing error and using error.Take seven－hole probe as an example，the quantitative calculation using computational fluid dynamics software is adopted to analyze the influence of the above three factors.Moreover，some detailed proposal are given on how to select appropriate probe，determine the conditions of use and assess measurement system error.

multi－hole probe；system error analysis；model error；manufacturing error；numerical simulation

V211.7

A

1672－9897（2012）05－0069－05

2011－09－20；

2011－11－09

国家973项目（2007CB714600）；国家自然科学基金 （11072112）；南航大青年创新基金（NS2010010）