小基阵双宽带源波束域相干信号子空间法研究

白晓娟，李亚安，张 伟，杨 涛，王瑞文

BAI Xiao-juan1,2,LI Ya-an1,ZHANG Wei1,YANG Tao2,WANG Rui-wen2

（1. 西北工业大学 航海学院，西安 710072；2. 中国人民解放军95997部队，北京 100076）

0 引言

研究对抗超低空飞行武装直升机的有效手段是现代化战争的迫切要求。由于雷达系统在低空目标探测方面受到很大的局限，因而，利用直升机飞行时发出的声音信号，根据声源定向技术，研究设计出一种无需人员值守的智能声探系统，从而实现对目标的自动检测、识别、定向和跟踪[1]。针对空气中单个声源的定向技术已相当成熟，并且在实际中得到应用，但现实中往往存在多个目标同时出现的情况，研究却相对较少。因此，研究典型的双目标同时出现的情况，对于实际工作中智能声探系统的实现有着深远的意义。目前，声源定向技术有三种基本方法，分别为基于最大输出功率的可控波束形成技术、基于声达时间差的定向技术[2]和基于高分辨率的方位估计技术。自20世纪70年代以来,高分辨方位估计一直是传感器阵列信号处理中的重要研究方向之一。

武装直升机飞行时的声音信号主要为低频宽带信号。对于两个宽带源定向问题的研究大多数运用阵元域的非相干信号子空间法（ICSM：InCoherent Signal-subspace Method）和相干信号子空间法(CSM：Coherent Signal-subspace Method)。其中， ICSM先将基阵接收到的宽带数据分解为若干个窄带分量,然后对各个窄带分量进行方位估计，最后对各个窄带分量估计的结果进行组合，从而实现宽带源的方位估计， 但是，ICSM方法处理不了相干信号宽带源的情况。CSM方法的定向原理是先把相干的宽带数据分解成若干窄带分量，然后利用聚焦矩阵(focussing matrix)，把各个频率分量聚焦到参考频率，最后采用窄带子空间法实现方位估计。相对于ICSM，CSM充分提取了各个子带中的信息，并且降低了检测与分辨信噪比门限，从而提高了方位估计精度。但二者均对系统误差太过灵敏，并且计算量比较大。波束域的算法能够降低分辨信噪比门限和计算量，并且可以增强抗系统误差的能力[3]。为了有效地对空气中运动的两个宽带源进行方位估计，本文以小尺度平面四元十字阵为基础，采用波束域相干信号子空间法(BSCSM：Beam Space Coherent Signal-subspace Method)进行处理。其中波束域处理运用常规波束方法[4]对信号源进行方位预估计，并在进行波束域方位估计时， 采用基于恒定束宽的宽带波束域高分辨算法以保证宽带信号在频带内的波束输出不出现失真。实验仿真了波束域相干信号子空间法(BSCSM)对双宽带信号源的方位估计及其定向性能，并与阵元域的相干信号子空间法(CSM：Coherent Signal-subspace Method)相比较，重点比较了统计意义上的误差和宽带平面波波达角度的角度分辨率等性能指标。

1 数学模型

声源被动定向的基本原理是利用空间布设的声学传感器阵元，接收目标声信息，然后结合有效的算法，从而对目标进行空间定向，如确定目标的方位角、俯仰角等。我们知道，目标声波抵达不同声学传感器阵元的路径各不相同，从而各个阵元接收的信号之间存在时间差，即时延，时延与目标声源的波达角度相关联，这一信息正是空气声被动定向系统进行声学定向的重要依据[5]。

一般情况下，由M个声学传感器阵元组成的空间声学传感器阵列，能够得到的独立时延数目为M-1[6]。相对于空气声被动探测系统，可以把超低空飞行的武装直升机看成点目标，该点目标具有三个自由度，要确定目标的方位，至少需要四个声学传感器阵元组成的空间基阵。十字形阵列具有分维特性，即二维参量可分开估计，且该阵列运算量较小。因此，选择平面四元十字阵作为空中运动目标声测被动定向系统的阵形。

平面四元十字形声学阵列接收远场两个宽带源辐射的信号，建立坐标系如图1所示[7]，其中二元线阵A、C和B、D相互正交,交点为坐标原点 。平面四元阵各阵元的直角坐标分别为A（d，0，0）、B（0，d，0）、C（-d，0，0）、D（0，-d，0）。远场宽带源M与接收基阵之间的距离远远大于阵元间距2d,则基阵接收的声源信号可以假设为平面波，声源的球坐标为M（r，q，j），P为M点在xoy 平面上的投影，则目标声源与坐标原点的距离为r，方位角为q（0°≤q<360°），俯仰角为j（0° ≤j≤90°）。我们知道，飞机一般是在起飞阶段进行预警的,所以，这里假定俯仰角j近似为90°，估计水平面xoy 内方位角q的大小。

若M元基阵接收D个宽带信号，其频域输出形式可以写成矩阵形式，表达式如下：

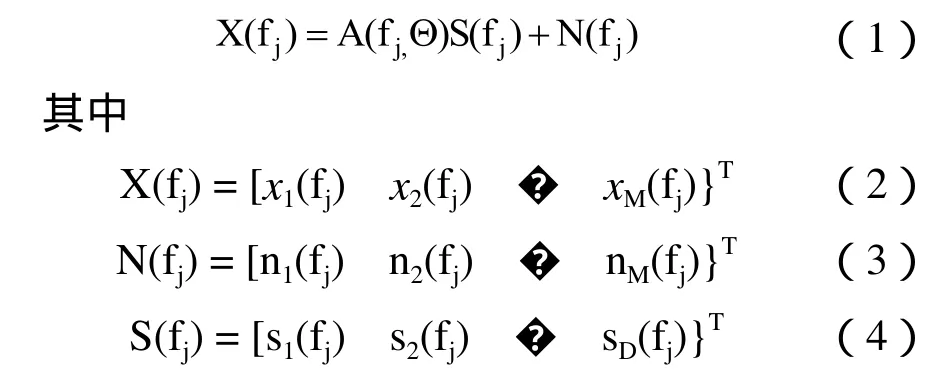
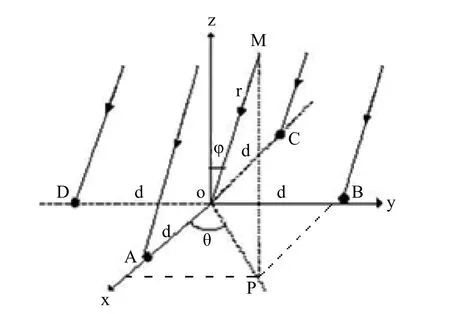
图1 平面四元十字形声学阵列接收远场信号示意图

分别表示基阵在参考点上对应频率fj的输出信号向量、加性白噪声向量和接收信号的傅立叶变换。表示对应频率fj和角度的阵列流形向量，= [q1,q2,,qD]表示D个信号的入射方向。

这里假定声学阵列接收到的信号与噪声互不相关，则与频率为fj对应时，基阵输出的互谱密度矩阵(Cross-Spectral Density Matrix)可表示为：

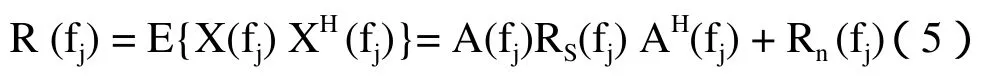
其中

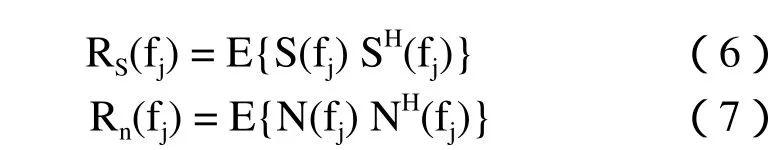
式中E为数学期望，H为向量或矩阵的共轭转置，RS(fj)为频率fj上信号自相关矩阵，Rn(fj)为频率 fj上噪声自相关函数。

针对基于平面四元声学阵列空气双宽带源方位估计问题，在频域上，先把基阵的频域输出分为 个窄子带，恒定束宽波束形成器的输出为

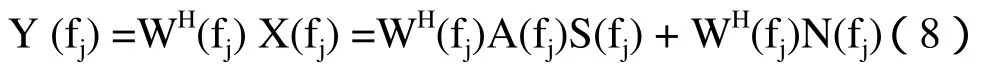
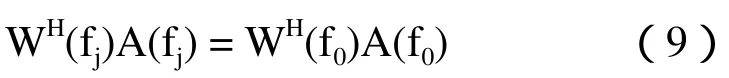
式中，f0为参考频率，上式即为恒定束宽设计所要满足的必备条件。由此可知，在设计频段内信号的波束输出出现不了失真现象。也就是说，当频段里束宽恒定的时候，可以得出平均互谱密度矩阵为

aj为对各个窄子带的互谱密度矩阵的标量加权因子。有

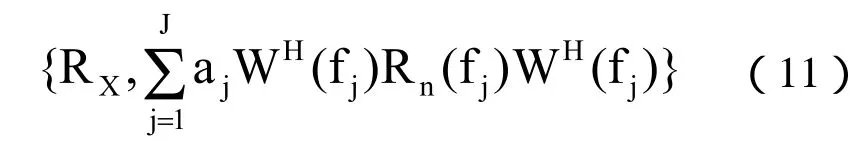
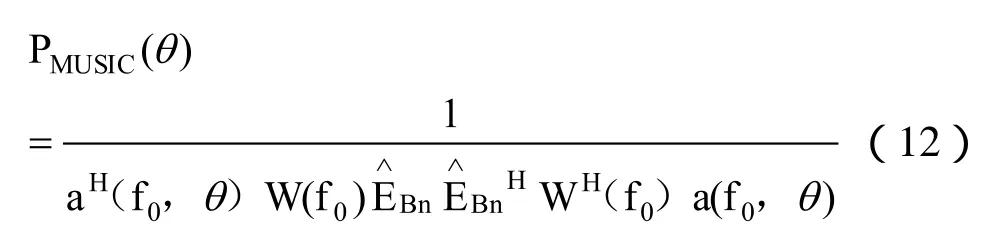
此时，方位谱的峰值就是宽带目标声源的入射方位的角度。

2 数值仿真试验和仿真结果分析

在以下仿真实验中，所用的基阵如图1，二元线阵阵元A与C以及B与D的间距均为1m，即d=0.5m。入射信号的模型为时间平稳的高斯随机过程，各个频率分量的功率在带宽内相等。

图2 直升机飞行声音波形

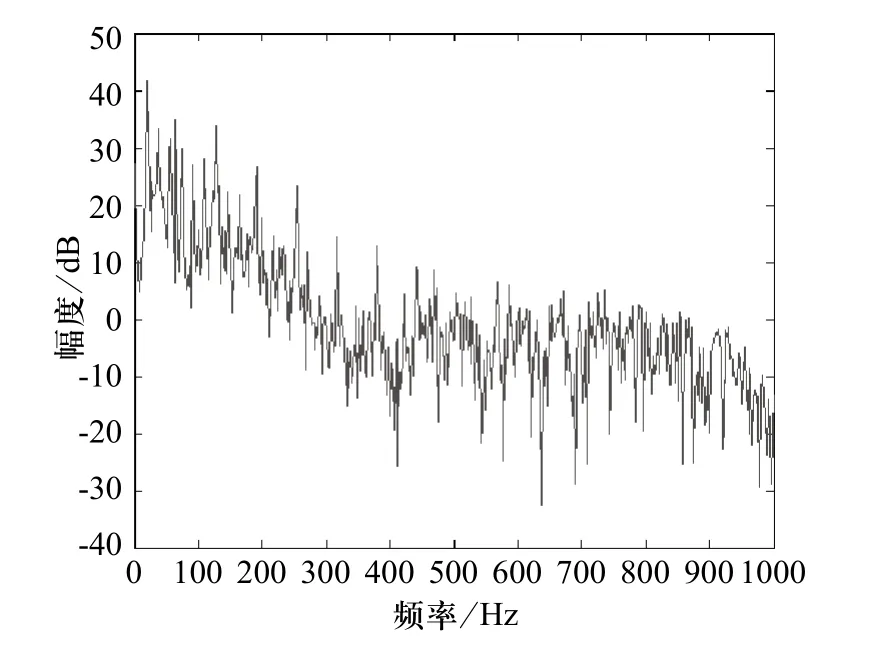
图3 超低空飞行武装直升机的噪声频谱

仿真过程中，为了得到与真实信号接近的数据，截取了一段实测的直升机噪声，在测试的过程中，采样率为10KHz，采样点数为1000点，其波形如图2所示。在频谱图中截取0～1000Hz之间的频谱，如图3所示，可以看出直升机噪声的能量主要集中在0Hz～250Hz范围内。将截取的直升机噪声作为参考点上的入射信号s(t)，针对基阵的各个阵元，仿真产生每个阵元上的入射信号，并在各个阵元上附加白噪声n(t) ,来调节信噪比SNR，从而得到基阵输出的采样数据x(t)。信号的入射方向q是能够任意选取的，并可以通过改变加性白噪声的功率来调节信噪比的大小。

由于基阵为平面四元十字阵，阵元个数比较少,基阵孔径也比较小,所以125Hz～175Hz 的宽带信号被分成20个窄子带，150Hz为参考频率。取两个宽带信号源的方位角为-5°和40°。平面四元阵在参考频率150Hz上的-3dB波束宽度为84°，即主瓣宽度比较宽，所以分别选取在0°、±60°、±120°预形成波束的多波束系统。5个方向上的波束均在20个窄子带上进行恒定束宽设计，图4～图6仅有指向 0°、60°和120°的波束图，-60°、-120°的波束图与60°、120°的波束图不仅对称，而且相同。从图中可以看出，指向-60°、-120°的恒定束宽波束没有指向0°的恒定束宽波束效果好，并且恒定束宽波束的旁瓣相对较高。

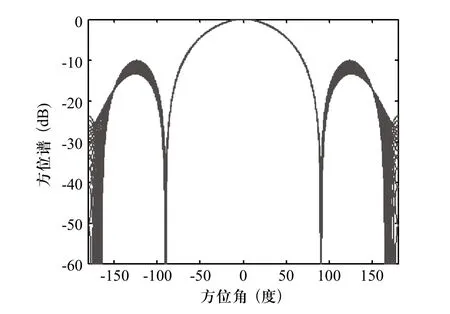
图4 指向0°，20个窄子带上恒定束宽波束图的叠加

另外，为了对比CSM和BSCSM两种方法的性能优劣，采用了CSM和BSCSM方法对在-5°、40°方向上的两个目标进行方位估计。仿真实验中，CSM采用的是旋转子空间不变的无聚焦损失方法，取＝ [-120° -60° 0° 60° 120° ]。

图7给出了两种方法估计的偏差，图8给出了两种方法估计的标准差，图中的偏差和标准差均为估计偏差和标准差的算术平均。可以看出，在信噪比较高时，BSCSM方法估计的偏差较CSM小，而标准差相当，即BSCSM方法估计较CSM性能好。

图5 指向60°，20个窄子带上恒定束宽波束图的叠加

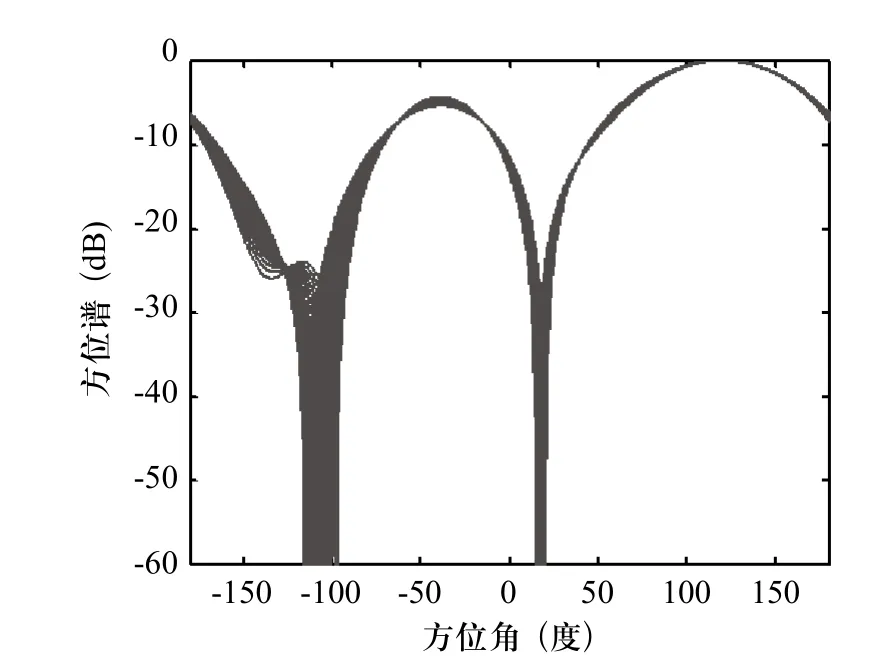
图6 指向120°，20个窄子带上恒定束宽波束图的叠加

图7 BSCSM和CSM方法标准差的比较

为了比较CSM和BSCSM对比较接近的两个宽带源的分辨能力，设定两个宽带信号源入射方向的方位角分别为-5°和40°，信噪比均为5dB，这里宽带信号源产生的方法同上。图9为分别用BSCSM和CSM两种方法对其进行估计的结果。

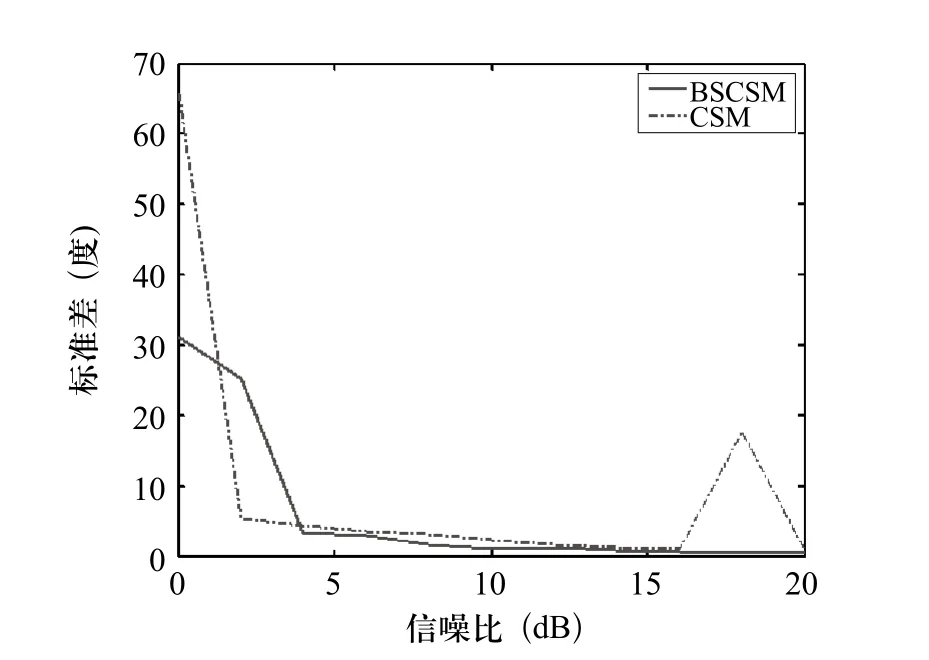
图8 BSCSM和CSM方法标准差的比较

从图9可以看出，采用BSCSM方法进行两个宽带信号源的方位角估计，对应的实曲线有两个峰值，分别为-5°和40°，即BSCSM法可以估计出两架直升机的方位角，分别为-5°和40°。而采CSM方法进行两个宽带信号源的方位角估计，对应的虚曲线只有一个峰值，介于-5°和40°之间 ，也就是说CSM无法分辨估计出两架直升机的方位角。由此可知，当两个信号源方位角的间隔一定小时， BSCSM可以分辨出两个信号源，而CSM不能，这说明BSCSM和CSM两种方法角度分辨率不一样，BSCSM比CSM的分辨率高，即波束域相干信号子空间法较阵元域相干信号子空间算法的优越性更高。

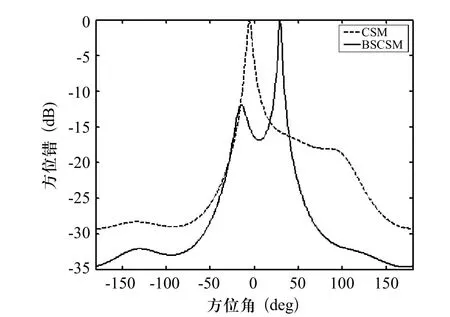
图9 BSCSM和CSM对两个信号方位角的估计

3 结论

本文基于远场环境下平面四元声学阵列，介绍了波束域相关信号子空间算法（BSCSM），利用了波束域处理能够增强抗系统误差和减小运算量的优势，采用该方法对两个宽带源进行方位估计并进行了仿真实验。从波束域相关信号子空间法（BSCSM）和阵元域相干信号子空间算法估计的标准离差和波达角度的角度分辨率来看,对于双宽带信号源，波束域相关信号子空间法在相同的处理频带上比阵元域的相干信号子空间法优越。

[1] 吴喜录,陈庆生,张元,等. 直升机目标声定位系统分析[J]. 南京理工大学学报,1996,20(6)： 521-524.

[2] 王昭,陈钟,赵俊渭,等. 空中运动目标时变时延估计方法的仿真研究[J]. 系统仿真学报,2002,14 (8)： 1049-1052.

[3] 鄢社锋,马远良. 传感器阵列波束优化设计及应用[M].北京： 科学出版社,2009.

[4] 刘道旭,严胜刚,杨志兴. 基于DSP的小型被动声定位系统[J]. 测控技术,2009,28(10)： 31-33.

[5] 马驰州,滕鹏晓,杨亦春,等. 分布式实时被动声定位系统研究[J]. 探测与控制学报,2007,29(1)： 18-22.

[6] 袁易全,雷家煜,姚治国. 近代声学基阵原理及应用[M].南京： 南京大学出版社,1994.

[7] 崔旭涛,何友,杨日杰. 时延估计多基地水下目标被动定位及误差分析[J]. 火力与指挥控制,2010,35(7)： 16-19.