酒糟微波间歇干燥特性及动力学模型

张黎骅，张 文，吕珍珍，徐中明

(1.重庆大学机械工程学院，重庆 610044； 2.四川农业大学信息与工程技术学院，四川 雅安 625014；3.四川农业大学食品学院，四川 雅安 625014)

酒糟微波间歇干燥特性及动力学模型

张黎骅1,2，张 文2，吕珍珍3，徐中明2

(1.重庆大学机械工程学院，重庆 610044； 2.四川农业大学信息与工程技术学院，四川 雅安 625014；3.四川农业大学食品学院，四川 雅安 625014)

利用自制的微波干燥在线测试装置，对酒糟的微波间歇干燥特性进行实验研究，探讨不同微波功率、糟层厚度及间歇比对酒糟湿基含水率、失水速率和温度的影响，得出酒糟微波间歇干燥的失水规律。根据实验数据建立酒糟微波间歇干燥的动力学模型，并对模型进行统计检验。结果表明，经拟合得到酒糟微波间歇干燥的最佳模型为Page模型，拟合方程为：ln (-lnMR)＝ -3.9977＋0.0038P-0.6427H-0.4118R ＋(1.7216 ＋ 0.0001P ＋0.0200H-0.0403R) lnt，此方程能够较好地描述酒糟的干燥过程，准确预测各阶段酒糟的含水率和失水速率。

酒糟；微波干燥；失水特性；动力学模型

由于微波干燥具有干燥速度快、热效率高、加热均匀、无污染和不破坏食品的营养成分等独特优点，使得微波干燥广泛应用于粮食、油料作物、茶叶、蚕茧及烟草等农产品加工中[1-4]。酒糟是酿酒的副产物。它以粮食为原料，富含大量粗蛋白、维生素、粗纤维等营养成分，尤其是粗蛋白的含量在12%以上[5]，经干燥后便是良好的饲料资源。酒糟深加工最关键的生产环节就是干燥，目前酒糟干燥主要采用直接干燥、压榨干燥等干燥方式[6-8]，其效率低、成本较高，很难满足生产需求。

对于农产品的干燥模型，国内有王俊等[9]、欧春艳等[10]，国外有 Ertekin等[11]、Hakan等[12]进行过相关研究。目前尚未有对酒糟的微波间歇干燥的报道，酒糟微波间歇干燥的理论研究还比较缺乏。本实验重点研究酒糟在微波间歇干燥条件下的干燥特性，探索微波功率、糟层厚度、间歇比对其干燥速率的影响规律，建立酒糟微波间歇干燥的动力学模型，预测酒糟在干燥过程含水率的变化，以期为酒糟微波间歇干燥工艺的研究提供理论依据，为酒糟干燥提出一种新的思路。

1 材料与方法

1.1 材料

实验所用酒糟购于雅安市大兴酒厂，为粮食、玉米和稻壳混合发酵酿酒后的副产物，呈散粒状，经初步脱水后湿基含水率为65%。然后按一定要求均匀平铺成一层在带孔塑料盘上；干燥过程中，定时采集物料质量，直至湿基含水率13%(安全贮藏水分)左右为止[6]。

1.2 仪器与设备

P70D20TL-D4型Galanz微波炉 佛山市格兰仕微波炉电器有限公司；GZX2DH型电热恒温干燥烘箱 上海跃进医疗器械厂；ARRW60电子精密天平 上海奥豪斯公司。

仪器设备组成如图1所示的实验系统，电子天平和温度传感器均与计算机连接，通过自编的Visual Basic应用程序在计算机上实时显示目前质量和温度并记录。考虑到酒糟取样的差异性，以上指标的实验重复3次，测量结果取平均值。

图1 微波干燥测试装置示意图Fig.1 Schematic diagram of online testing device for microwave drying

1.3 相关指标的计算

间歇比按式(1)进行计算[13]。

平均失水速率按式(2)进行计算[14]。

式中：Δm为相邻两次测量的质量变化/g；Δt为相邻两次测量的时间间隔/min。

1.4 微波间歇干燥的动力学模型

1.4.1 干燥模型

物料干燥是一个复杂的传热、传质过程，建立薄层干燥模型对研究干燥规律、预测干燥工艺参数有重要的作用[15]。目前，一般有3种数学模型用来描述物料薄层干燥过程[16]。

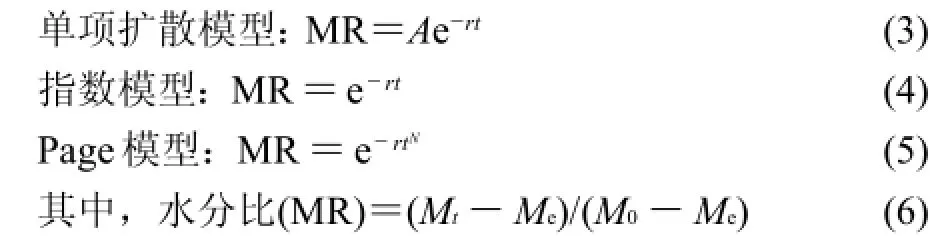
式中：t为干燥时间/min；Mt为t时刻物料的湿基含水率/%；Me为物料的湿基平衡含水率/%；M0为物料湿基初始含水率/%；A、r、N为待定系数。

由于微波干燥物料的湿基平衡含水率Me资料很少，实验数据很难获得，因此把上述的水分比(MR)简化为[3]：

1.4.2 模型的线性化

指数模型是单项扩散模型和Page模型的特殊形式，所以用单项扩散模型和Page模型来模拟酒糟的微波干燥过程[16]。将上述模型转化为线性模型：

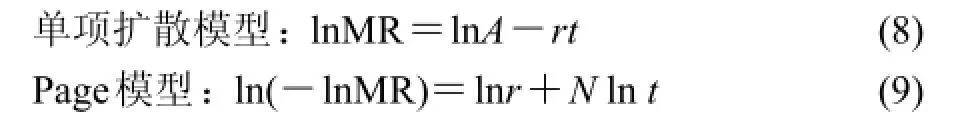
2 结果与分析

2.1 微波功率、糟层厚度及间歇比对酒糟干燥的影响

2.1.1 微波功率对酒糟失水特性的影响

当糟层厚度为10mm，装载质量为55g，微波间歇比为6时，不同微波功率条件下酒糟的干燥曲线和失水速率曲线如图2所示。

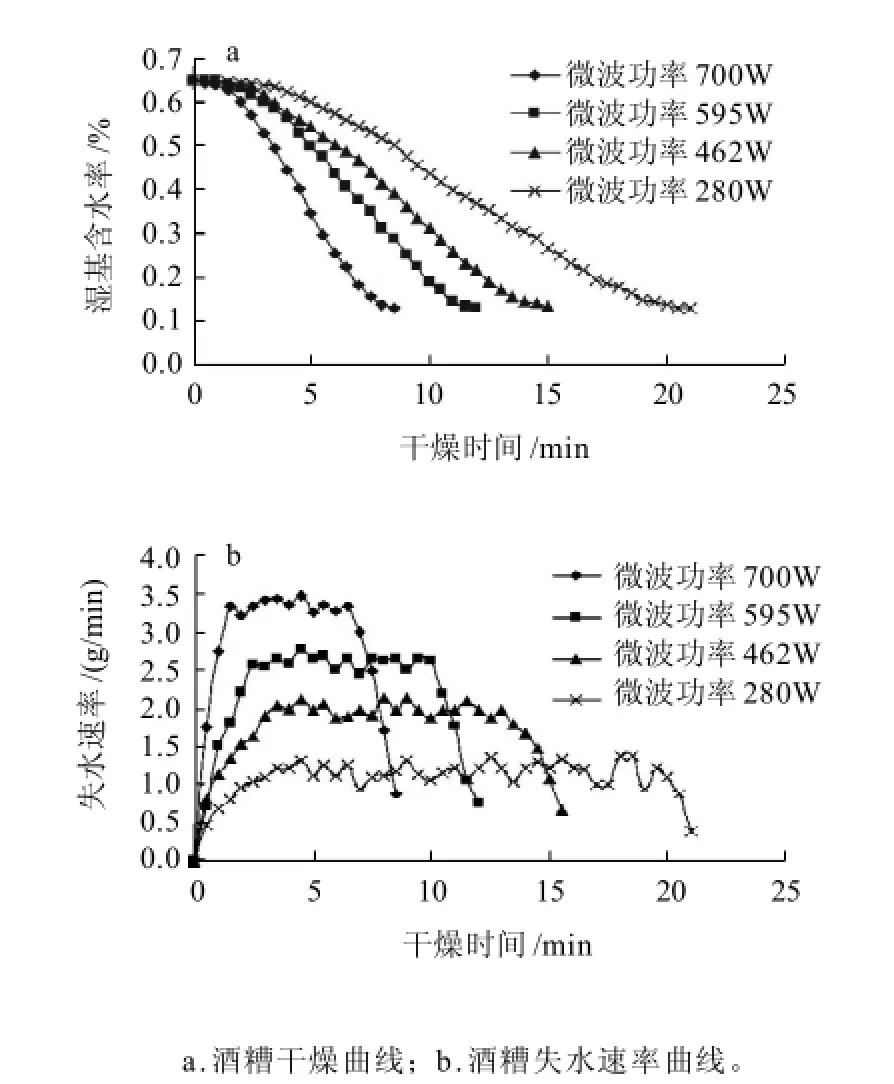
图2 不同微波功率下酒糟的干燥曲线和失水速率曲线Fig.2 Drying and dehydration rate curves of lees under different microwave powers

由图2a可知，随着微波功率的增大，酒糟的干燥曲线越陡，即微波强度越大，干燥速率越快，干燥至安全含水率所需的时间也越短。在干燥末期，曲线变平缓，微波干燥脱水难度增加。可见，在间歇比和层厚相同的条件下，干燥所需时间与微波功率大致呈负相关，微波功率越大，则干燥所需时间越短。

从图2b可以看出，酒糟微波间歇干燥过程同传统的干燥规律一样，可以分为3个阶段：加速、恒速及降速干燥阶段。微波干燥加速阶段时间短，且微波功率越大，进入恒速阶段所用的时间越少。失水速率随着微波功率的增大而增大，当微波功率从280W增大到700W，失水速率增大了160%。但当功率到280W时，恒速阶段失水速率急剧下降。

2.1.2 糟层厚度对酒糟失水特性的影响

当微波功率为595W，微波间歇比为6时，不同糟层厚度条件下酒糟的干燥曲线和失水速率曲线如图3所示。

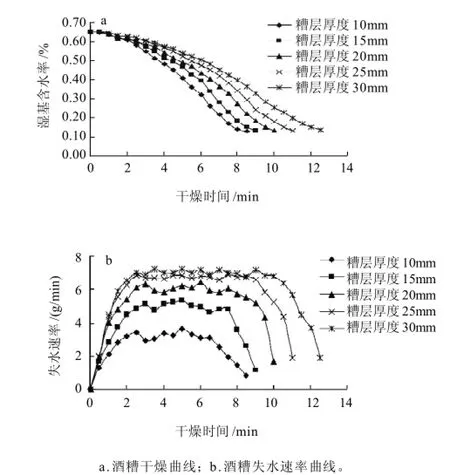
图3 不同糟层厚度下酒糟的干燥曲线和失水速率曲线Fig.3 Drying and dehydration rate curves of lees under different lees layer thicknesses

从图3可以看出，在不同糟层厚度的相同干燥条件下，其含水率变化是不相同的。糟层厚度越大，装载质量越多，在同一时刻其含水量越多，干燥至相同含水率的时间越长。糟层厚度增加10mm，干燥时间增加5%～15%。整个干燥过程分为了加速、恒速和降速干燥3个阶段，各阶段区别明显。糟层厚度越大，失水速率也越大，这是因为糟层厚度越大，微波是对物质整体加热利用率提高，使水分蒸发加剧，对总的干燥时间影响较小，因而失水速率增大。但当糟层厚度增大到30mm时，失水速率增大已不明显，这可能是因为厚度过大，影响了内部水分的扩散，使得水分蒸发速度变缓。反之，糟层厚度越小，失水速率越慢。

2.1.3 微波间歇比对酒糟失水特性的影响

在选择微波间歇比为1时干燥所得酒糟的品质均不理想，根据相关经验和预实验，单次干燥过程中微波接通时间定为8s，间歇时间为35～50s较为适宜，此时微波间歇比即为5.375～7.250。当微波功率为595W，装载质量为55g，糟层厚度为10mm时，不同糟层厚度条件下酒糟的干燥曲线、失水速率曲线和温度曲线如图4所示。

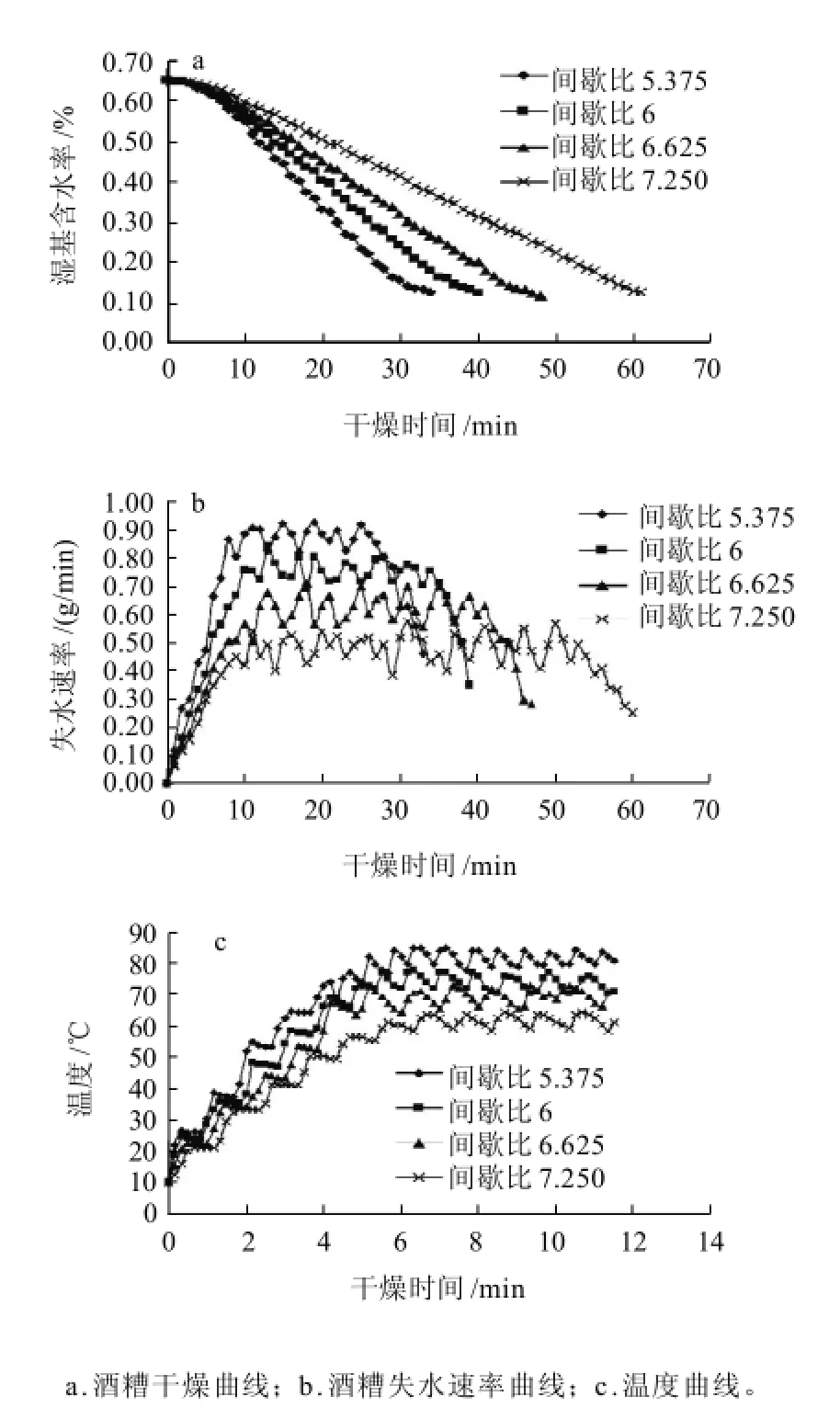
图4 不同间歇比条件下酒糟的干燥曲线、失水速率曲线和温度曲线Fig.4 Drying, dehydration rate and temperature curves of lees under different intermittent times

从图4b可看出，在微波间歇干燥时，干燥过程同样分为了加速、恒速和降速干燥3个阶段，但是在恒速干燥阶段时，干燥速率波动较大，这是微波间歇干燥同一般微波干燥的区别。从图4a可以看出，酒糟微波间歇干燥时，干燥时间明显增长，但是干燥品质得到了很好的保证。从图4c可以看出，在微波间歇干燥过程中酒糟的温度上升较慢，且最终维持在一固定温度处浮动，间歇比为6时，最高温度为75℃，间歇比为5.375时最高温度也仅为80℃左右，有效地避免了局部过热、打火和酒糟内部出现焦糊现象。间歇比越大，最终的稳定温度越低，品质越好，但干燥所需时间增多。

2.2 酒糟微波间歇干燥动力学模型的拟合

2.2.1 动力学模型的确定

根据实验数据分别绘制在不同微波功率、糟层厚度、间歇比下的-lnMR-t曲线和ln(-lnMR)-lnt曲线，结果如图5、6所示。

图5 不同微波功率、糟层厚度和间歇比条件下的-lnMR-t曲线Fig.5 -lnMR against t curves under different conditions of microwave power, lees layer thickness and intermittent time

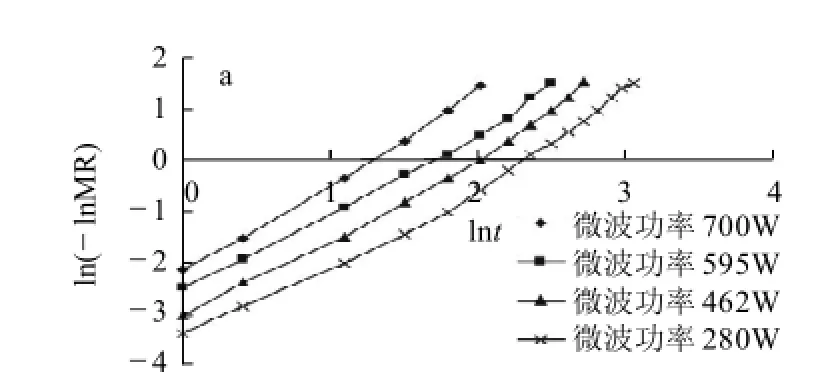
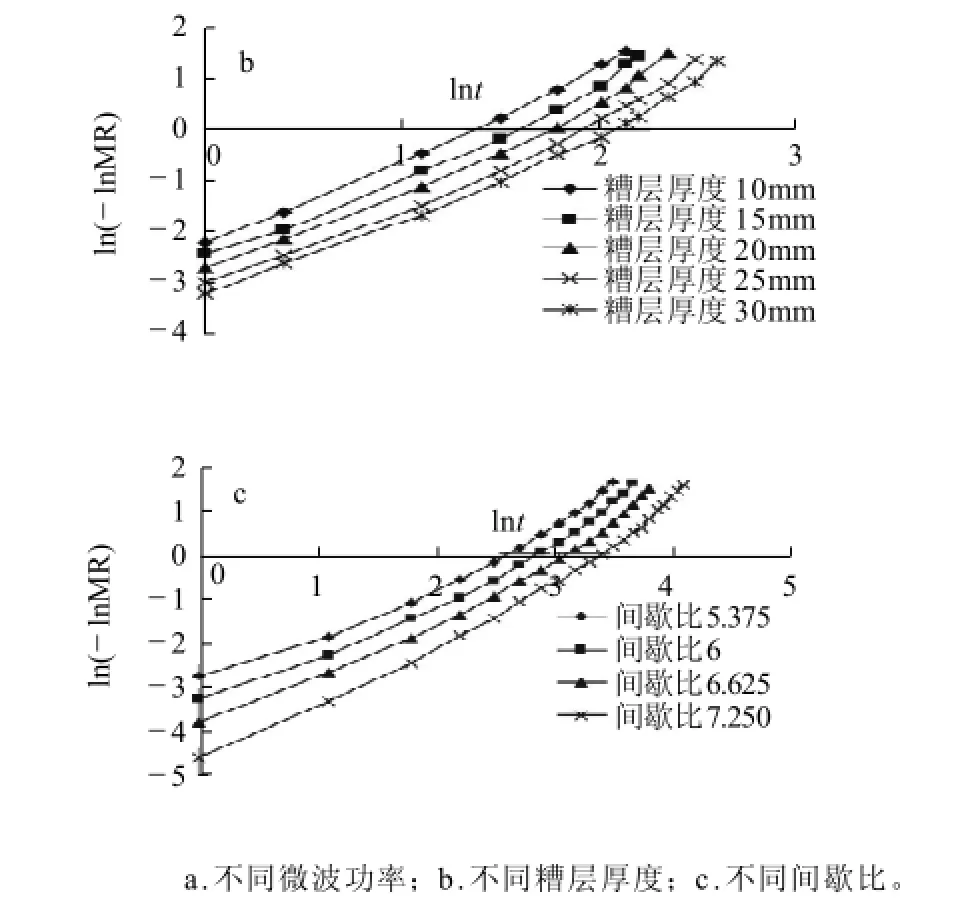
图6 不同微波功率、糟层厚度和间歇比条件下的ln(-lnMR)-lnt曲线Fig.6 ln(-lnMR)against lnt curves under different conditions of microwave power, lees layer thickness and intermittent time

从图5可看出，每条曲线在各点处的斜率是各不相同的，这说明-ln(MR)与时间t呈非线性关系，单项扩散模型与指数模型不适合微波干燥酒糟模型的建立。由图6可以看出，ln(-lnMR)与lnt呈线性关系，表明酒糟的微波间歇干燥过程可以用Page方程来描述。在不同微波功率、不同糟层厚度和不同间歇比下的ln(-lnMR)与lnt关系曲线基本平行且相互间存在较明显间距，说明微波功率、糟层厚度和间歇比对干燥模型影响显著。这与蒋玉萍等[17]研究微波干燥番薯片的结论相似。因此，选择Pag e模型作为酒糟微波间歇干燥的动力学模型。令：

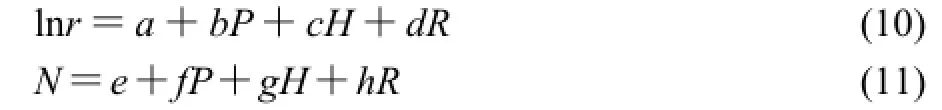
则有：

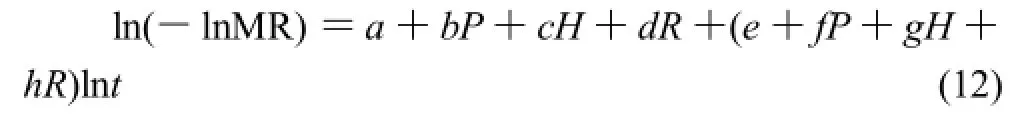
式中：P为微波功率/W；H为糟层厚度/mm；R为间歇比；a、b、c、d、e、f、g、h为待定系数。

用MATLAB软件进行数据处理，可求得酒糟微波间歇干燥的各待定系数，进而求得其动力学模型为：

2.2.2 模型的统计检验

为检验模型拟合效果，对上述模型进行统计检验，检验结果见表1。从表1可知，模型方差分析中，F＝898.90＞F0.01(8，127)＝2.65，表明模型显著；决定系数R2＝0.9801，拟合效果好。因此，可将该模型作为酒糟微波间歇干燥的数学模型，利用该模型可较准确地预测在不同干燥条件下，酒糟微波干燥过程中含水率和干燥速率的变化。

表1 模型的方差分析结果Table1 Analysis of variance for the model

2.2.3 动力学模型的验证

为进一步验证模型的准确性，任选一组实验进行验证，实验条件为：微波功率595W，糟层厚度20mm，微波间歇比为6。将该组实验值与模型预测值比较，见图7。

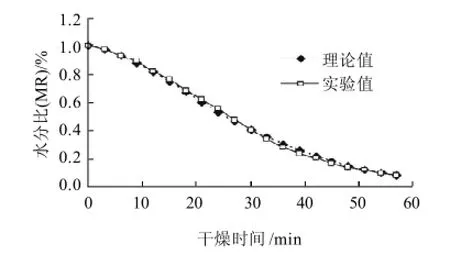
图7 水分比(MR)实验值与Page模型预测值的比较Fig.7 Experimental values and Page model-predicted values of MR

从图7可以看出，两条曲线基本吻合，说明Page方程能较准确反应水分的变化规律，可以用来描述酒糟微波间歇干燥的过程。

3 结 论

3.1 酒糟微波间歇干燥规律同传统的干燥规律一样，分为加速、恒速和降速干燥3个阶段。

3.2 微波功率、糟层厚度、间歇比对干燥过程影响均显著。微波功率、糟层厚度越大，间歇比越小，则干燥所需时间越短，但品质较差；反之越长，但品质能够得到保证。

3.3 用MATLAB软件进行回归分析，比较了3种常见的干燥模型，经拟合得到酒糟微波间歇干燥的最佳模型为Page模型，拟合方程为：ln(-lnMR)＝-3.9977＋0.0038P-0.6427H-0.4118R＋(1.7216＋0.0001P＋0.0200H-0.0403R)lnt。

利用上述实验结果，能够较好的预测各阶段酒糟微波间歇干燥的失水速率和含水率变化，为酒糟微波间歇干燥工艺提供理论依据。

[1]赵超, 陈建, 邱兵, 等. 花椒微波干燥特性试验[J]. 农业机械学报, 2007, 38(3): 99-101.

[2]刘志军, 张璧光, 李延军. 马尾松微波间歇干燥对干燥效率与速率的影响[J]. 木材工业, 2006, 20(4): 13-15.

[3]熊永森, 王俊, 王金双. 微波干制南瓜片干燥规律及工艺优化研究[J]. 农业工程学报, 2004, 20(2): 181-184.

[4]朱德泉, 王继先, 朱德文, 等. 香菜微波干燥的试验研究[J]. 农业工程学报, 2007, 23(12): 242-246.

[5]叶京生, 鲁林平. 啤酒糟干燥技术研究[J]. 干燥技术与设备, 2004, 3 (1): 38-39.

[6]夏萍. 气流换向干燥酒糟的试验研究[J]. 安徽农业大学学报, 2005, 32(1): 101-104.

[7]夏萍. 干燥工艺对酒糟干燥过程热效率的影响[J]. 包装与食品机械, 2004, 22(6): 27-29.

[8]冯殿义, 孙彤. 旋转闪蒸干燥器干燥酒糟过程的实验研究[J]. 化学工程, 2006, 34(2): 13-15.

[9]王俊, 许乃章. 热风、远红外和微波干燥香菇、蘑菇方程研究[J].农业机械学报, 1994, 25(2): 45-49.

[10]欧春艳, 杨磊, 李思东, 等. 甲壳素红外干燥特性及动力学模型研究[J]. 农业工程学报, 2008, 24(4): 287-289.

[11]ERTEKIN C, YALDIZ O. Drying of eggplant and selection of a suitable thin layer drying model[J]. Journal of Food Engineering, 2004, 63: 349-359.

[12]HAKAN O M, CAN E. Thin layer drying model for treated and untreated Stanley plums[J]. Energy Conversion and Management, 2006, 47: 2337-2348.

[13]曹崇文. 微波真空干燥技术现状[J]. 干燥技术与设备, 2004, 2(3): 5-9.

[14]赵超. 花椒间歇式微波干燥理论及工艺优化研究[D]. 重庆: 西南大学, 2006.

[15]黄艳, 黄建立, 郑宝东. 银耳微波真空干燥特性及动力学模型[J] . 农业工程学报, 2010, 26(4): 362-367.

[16]JARUK S, JOHN S R. Measuring moisture diffusivity of potato and carrot(core and cortex)during convective hot air and isothermal drying [J]. Journal of Food Engineering, 2006, 74(1): 143-152.

[17]蒋玉萍, 王俊. 番薯片微波干燥特性及干燥模型[J]. 浙江农业学报, 2009, 21(4): 407-410.

Intermittent Microwave Drying Properties and Kinetic Model of Lees

ZHANG Li-hua1,2，ZHANG Wen2，LU.. Zhen-zhen3，XU Zhong-ming2
(1. College of Mechanical Engineering, Chongqing University, Chongqing 610044, China；2. College of Information and Engineering Technology, Sichuan Agricultural University，Ya’an 625014, China；3. College of Food Science, Sichuan Agricultural University, Ya’an 625014, China)

A self-made online testing device for microwave drying was used to dry lees for exploring its batch drying properties. The effects of microwave power, lees layer thickness and intermittent time on moisture content, drying rate and temperature were investigated. The dehydrating law of lees was achieved during intermittent microwave drying. A kinetic model for intermittent microwave drying was established based on experimental data as follows: ln (-lnMR)＝ -3.9977＋0.0038P-0.6427H-0.4118R ＋(1.7216 ＋ 0.0001P ＋0.0200H-0.0403R) lnt. The kinetic model could accurately describe drying process of lees and predict water content and drying rate.

lees；microwave drying；dehydration characteristics；kinetic model

TS261.3

A

1002-6630(2012)01-0087-05

2011-02-25

国家现代农业(肉牛牦牛)产业技术体系建设专项(CARS-38)；四川省学术与技术带头人培养基金资助项目

张黎骅(1969— )，男，副教授，博士研究生，主要从事农产品加工机械与装备研究。E-mail：zhanglihua69@126.com