摇摆条件下窄通道内单相水流态转捩特性

阎昌琪，幸奠川，曹夏昕，谢清清，2

(1.哈尔滨工程大学核安全与仿真技术国防重点学科实验室，黑龙江哈尔滨150001;2.中国核动力研究设计院，四川成都610041)

矩形窄缝流道因其换热面积大，设备结构紧凑，沸腾过热度低等优点在很多工程领域内得到了实际应用，如航空航天，热能动力设备，船舶动力系统，大型集成电路冷却等.国内外学者对稳态窄矩形通道内单相流动特性展开了大量研究［1-2］，但对非稳态条件下矩形通道内流动特性的研究较少.

在非稳态动力系统中，工质流体流动特性会发生改变.文献［3-4］对摇摆条件下圆管内单相水绝热流动特性做了一定的研究，但主要集中在湍流区.幸奠川等对摇摆条件下矩形通道内层流区和湍流区单相水绝热流动特性进行了实验研究，但未对过渡区流态转捩特性做细致分析［5-6］.过渡区局部流动特性的轻微改变难以造成压差等参数的明显变化，因此，摇摆条件下窄通道内单相水临界点附近的流动特性尚不明确.可视化流迹显示方法因具有直观可靠，成本低廉等特点而被研究者用以显示流动特性［7-8］.本文采用示踪剂，直观的揭示了摇摆对临界点附近流动特性的影响机理.

1 摇摆台及实验回路简介

本文采用的摇摆台与文献［9］相同，摇摆台的运动规律为

式中:θ、ω和β分别为t时刻的角位移(逆时针为正)、角速度和角加速度;θm、T和f分别为摇摆振幅，摇摆周期和摇摆频率(T=1/f).本实验摇摆工况组合为(按θm～T的表示方式):10°～8 s、10°～12 s、10°～16 s、15°～16 s、30°～16 s.

实验回路如图1所示，实验中用高位水箱提供压头以获得稳定的流量及恒定的压头.示踪剂为红墨水与酒精按1∶4的混合溶液，以保证和实验工质密度接近(纯净水).流动阻力特性实验采集的参数包括实验段流量、水温及测压孔间压降.可视化流迹显示实验时，待流动稳定后记录实验参数，采用尼康D200单反相机拍摄照片.流量和压降信号通过NI SCXI-1338模块与计算机采集系统实时采集;温度采用二级标准温度计在实验段出口取样测量，误差为±0.1℃.压差变送器(CECCS43:0～10 kPa)精度为0.2级.流量计(Promass 83:0～4 000 kg/h)测量精度为±0.1%.实验件为光滑的有机玻璃矩形通道(2 mm ×40 mm×2 000 mm)，其中2个测压孔间距1 600 mm，下测压孔距入口200 mm，示踪剂注入孔距入口800 mm.Re变化范围为200～21 000，但重点集中在2 000～3 500.

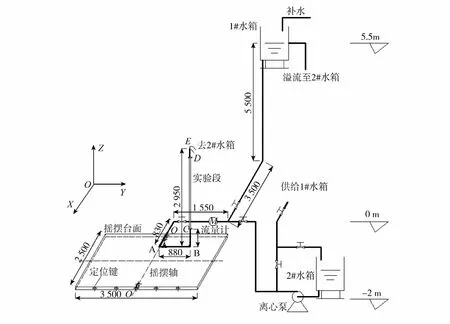
图1 实验回路示意Fig.1 Schematic diagram of experimental loop

2 阻力特性实验结果

稳定竖直状态下，临界Re大约在2 550左右，见图2.摇摆条件下平均摩阻系数曲线转折临界点随摇摆工况的不同而变化.平均摩阻系数转折点随摇摆周期的变化不明显，随摇摆振幅的增加而有所提前.当Re小于2 400(稳定的层流区)或者大于3 500(湍流区)时，摇摆对平均摩阻特性没有明显影响.Re介于2 400～3 500的过渡区时，不同摇摆工况下平均摩阻系数存在微小差别，但总体上变化不大，为进一步确定摇摆对临界点附近流动特性的影响，还需进行可视化流迹显示实验.

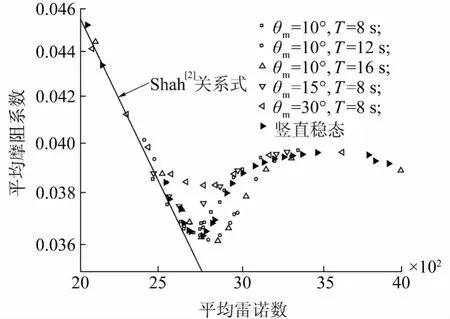
图2 摇摆条件下平均摩阻系数Fig.2 Mean friction coefficient under rolling condition

3 可视化研究结果及分析

3.1 可视化实验结果

稳定竖直状态下典型流态对应的示踪剂如图3所示.当Re小于2 550时，示踪剂为一条清晰的沿流动方向的细直线，不与周围流层发生水动力学搅浑，如图3(a)，此时通道内为典型的稳定层流.当Re大于3 500时，示踪剂迅速向四周均匀扩散，水流被均匀染色，此时流体质点发生剧烈的横向搅浑，动量和能量传递使得染色剂迅速与周围流体混合，通道内为典型的湍流，如图3(c).由前文摩阻实验可知，稳态条件下临界Re大约在2 550左右.从Re为2 550开始，逐渐增加流量，到相应的Re为2 563时，示踪剂在不确定的位置随机出现小波动，但波动极为不稳定，迅速回到直线状态，表明层流流动已经失稳，难以维持原状，然而稳定的湍流状态尚未形成，判定此时为过渡流起始状态，如图3(b).

在图3(b)所示的状态下，启动摇摆台，在其运动的正向最大角度，负向最大角度和平衡位置3个特征位置处拍摄示踪剂的流动特征.10°～16 s摇摆工况下的示踪剂形状如图4所示.显然在正向最大摇摆角位置处通道内为典型的层流，流态转捩受到抑制;平衡位置处和竖直稳态相似，摇摆对其影响不明显;在负向最大摇摆角位置处示踪剂迹线波动相对于稳定竖直状态有所加强，此处转捩受到促进.实验观察到摇摆工况为10°～8 s和10°～12 s时的示踪剂流动特征与图4相同，说明在一定幅度内改变摇摆周期对窄通道内单相水流态转捩没有明显影响.

图3 非摇摆状态下流型Fig.3 Flow regimes under non-rolling condition

图4 摇摆状态下流迹(10°～16 s，Re=2 563)Fig.4 Flow regimes in rolling condition(10°～16 s，Re=2 563)

摇摆周期为16 s，最大摇摆角度为10°，15°和30°时，正向最大摇摆角度位置处示踪剂流动特征始终如图3(a)所示的细直线，对应的流态为层流.负向最大摇摆角位置处示踪剂随摇摆振幅的变化见图5.由图5可见，负向最大角度位置处示踪剂横向扩散随着摇摆振幅的增加而加剧.摇摆振幅10°时扰动发生后迅速消失，示踪剂恢复为细直线;摇摆振幅15°时，扰动在拍摄区内不能消失，但横向扩散不均匀，未形成图3(c)所示的湍流;摇摆振幅30°时，横向扩散已比较均匀，湍流形成.摇摆振幅越大，对负向最大摇摆角度位置处的流态转捩促进作用越强.

较小的摇摆振幅对平衡位置处示踪剂没有明显影响，示踪剂流迹与图3(b)十分相似.摇摆振幅30°时，平衡位置处示踪剂横向波动比稳定状态下剧烈，摇摆促进此处转捩发生，见图6.

图5 负向最大摇摆角位置处流迹(T=16 s，Re=2 563)Fig.5 Flow regimes at the positions of negative maximal rolling angle(T=16 s，Re=2 563)

图6 平衡位置处流迹(30°～16 s，Re=2 563)Fig.6 Flow regimes at the balance positions(30°～16 s，Re=2 563)

3.2 摇摆对流态转折影响的机理解释

文献［10］给出了摇摆条件下附加压降的积分关系式:

式中:下标1和2分别表示积分的起点和终点.对本实验回路(见图1)，仅AB和BE两段内附加惯性力沿流动方向分量不为零.因此，摇摆条件下回路总的附加压降为

整个回路运动部分(AB段与BE段)重位压降为

结合图1所示实验回路尺寸，摇摆条件下回路运动部分附加压降及重位压降见图7.

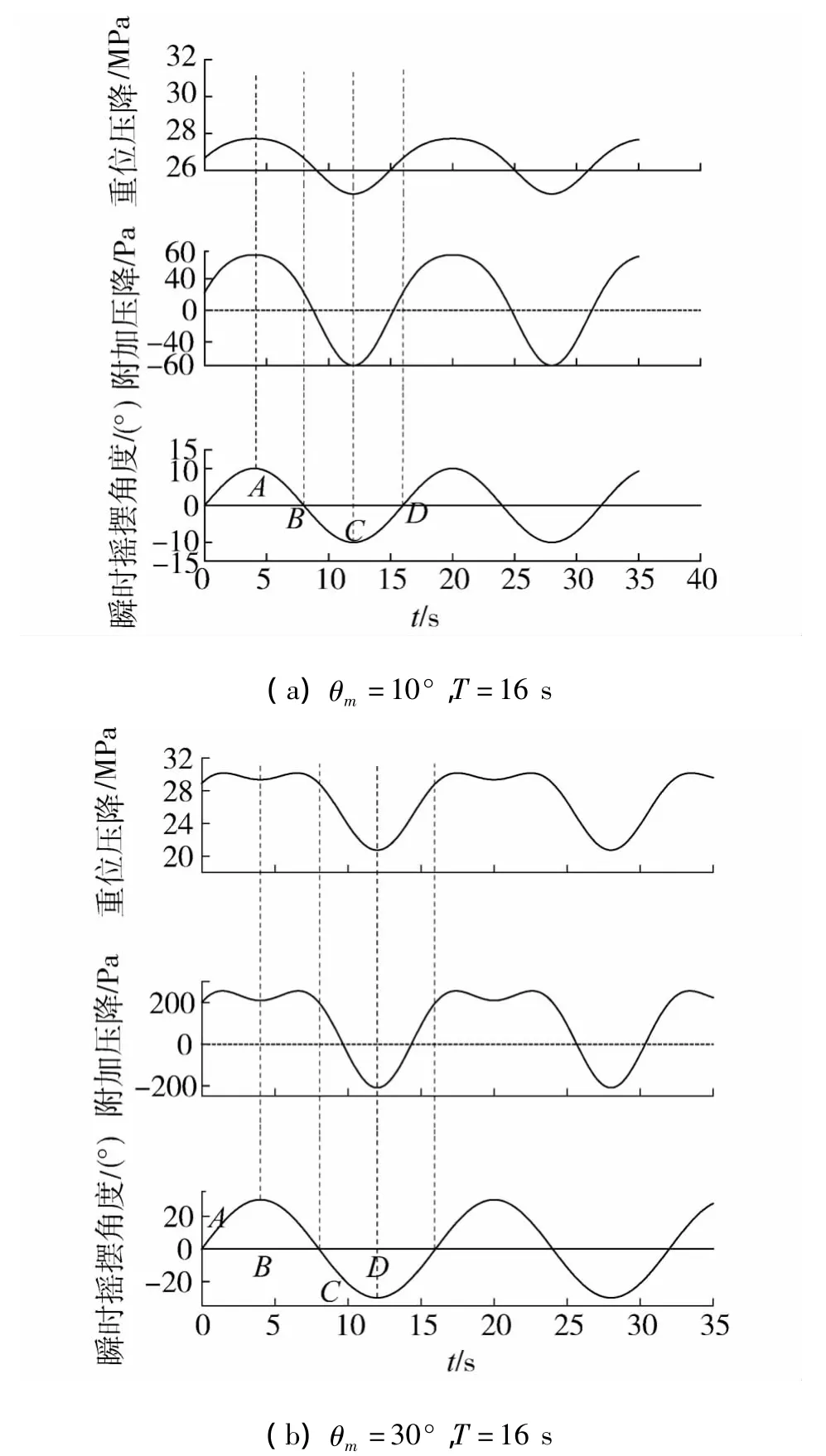
图7 摇摆条件下回路总附加压降和重位压降Fig.7 The total additional and gravity pressure drop under rolling condition

由图7及式(5)可见，摇摆条件下回路总的附加压降和重位压降的波动周期等于摇摆周期.摇摆台处于正向最大角度时(A点)，附加压降及重位压降均处于最大值(30°时接近最大值)，附加压降为正，驱动流动.相对于稳定竖直状态，重位压降的增加值(10°时1 074 Pa;30°时532 Pa)大于附加压降(10°时70 Pa;30°时209 Pa).回路驱动压头恒定，摩擦压降变化很小，此时回路总阻力增大导致流速减小，因此摇摆始终抑制正向最大角位置处流态转捩.摇摆台处于负向最大角位置时(C点)，重位压降处于最小值，附加压降处于负向最大值，阻碍流动.相对于稳定竖直状态重位压降减小量(10°时1 912 Pa;30°时8 076 Pa)远大于附加压降的绝对值(10°时70 Pa;30°时209 Pa)，此时回路总阻力大大减小从而流速增加，摇摆促进此处流动转捩.摇摆振幅越大，相对于竖直稳态负向最大摇摆角位置处回路总阻力越小，摇摆对流态转捩的促进作用越强.摇摆台位于平衡位置时(B和D点)重位压降和竖直稳态相同，附加压降为正，驱动流动.摇摆振幅10°和15°时附加压降分别为22.4 Pa和50.1 Pa，对流动影响不明显;振幅为30°时，附加压降为196 Pa，驱动作用已经比较明显，因此相应的示踪剂横向扩散比稳态剧烈.

摇摆台从正负两个方向经过平衡位置时(B或D)附加压降和重位压降相同，因此摇摆方向对平衡位置处转捩特性没有影响.改变摇摆周期仅仅相当于将图7中各曲线沿时间轴拉伸或者压缩，对附加压降幅值的影响很小，因此改变摇摆周期对流态转捩没有明显影响.

4 结论

1)实验结果表明稳定状态下本实验段临界Re大约为2 550.Re小于2 400或大于3 500时，摇摆对矩形窄通道内单相水流态没有明显影响，但摇摆运动对临界点附近流动特性有一定的影响.

2)摇摆运动始终抑制正向最大摇摆角位置处的流动，促进负向最大摇摆角度位置处的流动，摇摆振幅较小时对平衡位置处流动的促进作用不明显.

3)负向最大摆角位置处增加摇摆振幅可促进流态转捩，摇摆周期在一定范围内对流态转捩没有明显影响.

4)摇摆对流态转捩的影响主要是通过改变整个回路有效重位压降及造成整个回路附加压降体现出来的，前者为主要影响因素.

［1］STEINKE M E，KANDLIKAR S G.Single-phase liquid friction factors in microchannels［J］.International Journal of Thermal Sciences，2006，45(11):1073-1083.

［2］HARNETT J P，KOSTIC M.Heat transfer to Newtonian and non-Newtonian fluids in rectangular ducts［J］.Adv Heat Transfer，1989，19:247-356.

［3］曹夏昕，阎昌琪，孙立成，等.摇摆状态下竖直管内单相水摩擦压降特性分析［J］.哈尔滨工程大学学报，2006，27(6):834-838.

CAO Xiaxin，YAN Changqi，SUN Licheng，et al.Analysis of pressure drop characteristics of single-phase flowing through vertical rolling pipes［J］.Journal of Harbin Engineering University，2006，27(6):834-838.

［4］ZHANG J H，YAN C Q，GAO P Z.Characteristics of pressure drop and correlation of friction factors for single-phase flow in rolling horizontal pipe［J］.Journal of Hydrodynamics，2009，21(5):614-621.

［5］幸奠川，阎昌琪，刘洋，等.摇摆条件下矩形通道内单相水强制循环流动特性研究［J］.核动力工程，2011，32 (1):112-116.

XING Dianchuan，YAN Changqi，LIU Yang，et al.Research on single-phase forced circulation in rectangular channel flow characteristics under rolling condition［J］.Nuclear Power Engineering，2011，32(1):112-116.

［6］幸奠川，阎昌琪，曹夏昕，等.摇摆条件下单相水强制循环阻力特性实验研究［J］.原子能科学技术，2011，45 (6):672-676.

XING Dianchuan，YAN Changqi，CAO Xiaxin，et al.Experimental study on forced circulation resistance characteristics of single-phase water flow under rolling condition［J］.Atomic Energy Science and Technology，2011，45(6): 672-676.

［7］唐大伟，张春平，曲伟.矩形微通道内流场的可视化实验研究［J］.华中科技大学学报:自然科学版，2007，35 (11):24-27.

TANG Dawei，ZHANG Chunping，QU Wei.Visualization experiments of flow field in rectangular microchannels［J］.Journal of Huazhong University of Science＆Technology: Nature Science Edition，2007，35(11):24-27.

［8］LIU Z，ZHAO Y.Experimental study on visualization of the flow field in microtube［J］.Science in China:Ser E，2005，48(5):521-529.

［9］XING Dianchuan，YAN Changqi，SUN Licheng，et al.Effects of rolling on characteristics of single-phase water flow in narrow rectangular ducts［J］.Nuclear Engineering and Design，2012，247:221-229.

［10］高璞珍，庞凤阁，王兆祥.核动力装置一回路冷却剂受海洋条件影响的数学模型［J］.哈尔滨工程大学学报，1997，18(1):24-27.

GAO Puzhen，PANG Fengge，WANG Zhaoxiang.Mathematical model of primary coolant in nuclear power plant influenced by ocean conditions［J］.Journal of Harbin Engineering University，1997，18(1):24-27.