可重构机器人构形平面的工作空间研究

魏延辉，刘施菲，许德新

(哈尔滨工程大学自动化学院，黑龙江哈尔滨150001)

可重构机器人能够以一套机器人模块，产生多种工作构形，克服传统固定结构形式的工业机器人改装费用高，不能一机多用等缺点，可满足快速实时的生产生活需要，近年来成为国内外机器人研究的热点之一［1-2］.

运动学求解问题是可重构机器人研究的关键问题之一.目前研究的方法大多采用旋量和指数积的方法进行求解［3-4］，这种方法可以不依赖与机器人构形形式，但是其求解过程较为复杂，目前仅能解决少自由度的工作构形运动求解.由于可重构机器人在实际的应用中，找到一组满足要求的运动学解即可，无需将所有的运动学正逆解求出来.因此采用构形平面匹配的方法，能够在较为合理的工作位形下求解出可重构机器人运动学解，这种方式更能够满足可重构机器人在实际生产下的需要［5-6］.

构形平面方法求解运动学的一个重要部分是划分后的构形平面的工作空间求解，它是构形平面进行匹配的前提.由于可重构机器人的实时性需要，要求运动学求解的计算量尽可能小，而构形平面进行位置和姿态匹配时，也不需要将整个构形平面的工作空间完全表示出来，因此在工作空间的求解计算上，希望表达方式尽可能简洁、计算量小，仅将构形平面匹配需要的工作空间表示出来即可.可重构机器人构形复杂多变，划分后的构形平面的工作空间会形成多连域封闭形式区域，求解较为困难，本文力求实现自动快速求解构形平面的工作空间的方法.

1 构形平面定义

1.1 基本模块的数学建模

可重构机器人基本模块可划分为4种:移动模块、摇摆模块、回转模块和连接模块.基于可重构机器人模块化思想，为每个基本模块建立运动学模型，运动模块仅有一个变量，而连接模块无变量，模块间的连接定位用连接机构保证.为了方便表达，建立可重构机器人模块的统一表达方式:

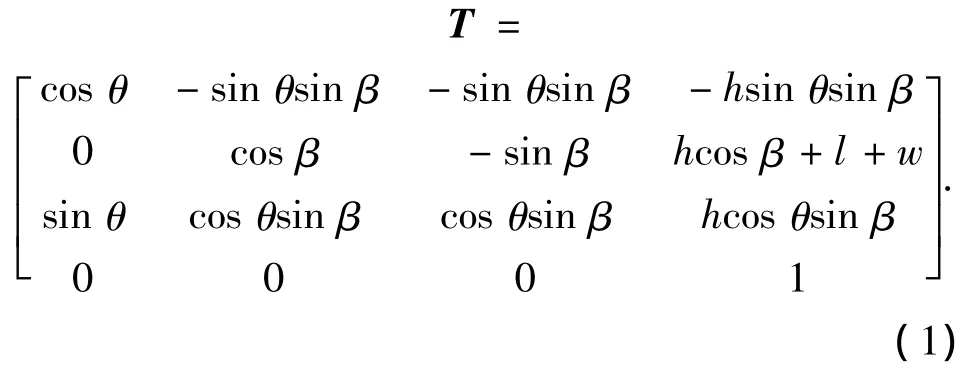
式中:θ为该模块是回转模块时的回转角度，若为其他模块时为0;β为该模块是摇摆模块时的摆动角度，若为其他模块时为0;h为该模块是摇摆模块时的连接长度，若为其他模块时为0;l为该模块是回转模块或连接模块时的连接长度，若为其他模块时为0;w为该模块是移动模块时的移动量，若为其他模块时为0.

1.2 构形平面的定义

根据基本模块的统一表达方式，通过位姿矩阵相乘表达式，可以发现摇摆模块、移动模块和连接模块单独或任意组合组成机器人构形，无论运动模块如何运动，所得到的机器人末端仅能在二维平面内运动;而机器人构形中含有摇摆模块和回转模块，并同时有转动量时，机器人末端可在三维空间能运动.可以认为可重构机器人在某一时刻的位形可由有限个平面依次连接组成.

定义1 构形平面:若干个依次连接的可重构机器人模块的中心线所形成的平面称为构形平面.

构形平面具有如下的特点:机器人某时刻位形由1个或多个构形平面组成，相邻2个构形平面的交线必是回转模块的中心线.

1.3 构形平面的划分

按照构形平面的特点，以回转模块在机器人构形中的位置作为划分构形平面依据.可将机器人构形用若干个构形平面组成，其最大数量取决于构形中回转模块的数量.

定义2 构形平面中心:在构形平面内，在与该构形平面相邻的上一个构形平面相交的回转轴线上，与上一个相邻构形平面最近的摇摆中心定义为构形平面中心.

由于第1个构形平面没有与之相邻的上一个构形平面，因此它的平面构形中心就是基座标原点.

定义3 构形平面末端:在构形平面内，在与该构形平面相邻的下一个构形平面相交的回转轴中心线上，与本构形平面最近的摇摆中心定义为构形平面末端.

由于最后一个构形平面没有与之相邻的下一个构形平面，因此它的平面构形末端就是机器人的末端点.

值得说明的是，在划分的构形平面内除了构形平面中心和构形平面末端所占有的回转模块外，还会有其他的回转模块.由于构形平面在匹配时是以平面方式匹配，因此构形平面中的这种回转模块可近似看作是连接模块，以保持构形平面的平面性.

1.4 平面构形的逆运动求解方法

构形平面工作空间的区间计算需要对平面构形进行逆运动学求解，其方法也有别于机器人的运动学求解.构形平面在匹配时，构形平面的末端及相应连杆的姿态和位置相对其中心是已知的，这样运用平面构形的逆运动进行区间计算时，仅需要判断机器人关节能否在其工作区间内满足要求.

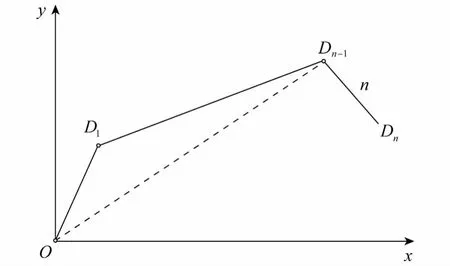
图1 平面构形求解示意Fig.1 Sketch of solving configuration plane

如图1所示图中DnDn－1姿态和Dn点位置已知，则Dn－1位置也是已知的，则ODn－1线段距离也是已知的.以求解摇摆中心为 D1的关节为例，在△OD1Dn－1中，由余弦定理可求得∠OD1Dn－1的值，若所求的值在该关节的运动范围内，则其他关节不用计算，可认为其没有进行转动，关节角为零.否则使该关节的关节角等于其极限角，进行求解下一个关节的关节角，直到除了第1个关节和第n个关节以外，构形平面内所有的关节角都用采用这种方法求解出.这样D1点的位置就已知了，这样在构形平面内，ODn－1和OD1两端的矢量也就已知了，从而可求得第1个关节的关节角，由于β1+β2+…+βn是已知的，这样βn也就已知了.

值得说明的是，对于移动模块的移动量求解，当求解到含有移动模块关节的关节角时，要进行判断一下，能否通过移动模块解决位置匹配.若能够，则不用进行剩余关节角的求解，将移动模块的置于相应的移动量处.否则将其移动量放在最短处和最长处(由该关节中心到n－1关节中心距离决定)，进行下一个摇摆关节的求解.

2 构形平面工作空间计算方法的研究

2.1 典型构形平面工作空间分析

在划分后的构形平面上，由于分布的模块种类和数量的差异，所形成的工作空间也有很大差异.根据平面构形末端相对于平面构形中心的距离和姿态角的关系，有下面几种典型情况:

1)距离不变、姿态角不变.平面内可能有回转模块和连接模块，其工作空间仅为一个点.

2)距离变化、姿态角不变.平面内不仅可能有回转模块和连接模块，还必须有移动模块.其工作空间为一条直线.

3)距离不变、姿态角变化.平面内不仅可能有回转模块和连接模块，并且有且只有一个摇摆模块.其工作空间为一段圆弧.

4)距离变化、姿态角变化.平面内可能有回转模块和连接模块，还有移动模块加摇摆模块组合或者2个摇摆模块的组合.其工作空间为不规则的平面.

2.2 构形平面工作空间边界的计算

前3种类型构形平面的工作空间容易表示，其位置多在整个机器人构形的最前端和最后端，在构形平面匹配时一些参数容易确定，也容易匹配.由于设计的摇摆模块是非偏置形式的，这种形式模块的运动空间是有限制的，从而造成了最后一种类型构形平面的工作空间是不规则的，在进行匹配时既要考虑位置是否匹配，而且要考虑各关节角是否满足要求.在构形平面内移动模块和摇摆模块决定工作空间大小.

第4种类型构形平面是研究的重点，采用极坐标的形式表示平面构形的工作空间，首先在给定任意极坐标角下，采用构形平面内的机器人末端点到构形中心最大值和最小值，以便进行多连域工作空间区间的搜索.

1)极坐标角下最大值的求解.当目标矢量的极坐标角未超出第1个摇摆模块运动范围，则其最大值为

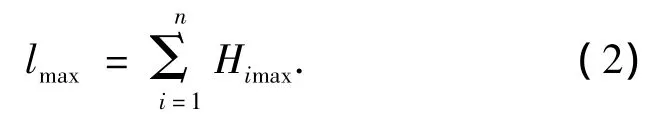
当目标矢量的极坐标角超出第1个摇摆模块运动范围时，如图2所示，D'B为其余关节最大长度和，首先将第1个关节置于距离极坐标角最近的极限角，然后将第2个摇摆关节置于与第1个摇摆关节相同的极限角处，求解D'的位置坐标，查看其极坐标角与第1个摇摆关节的极限角是否分布在目标极坐标矢量的两侧.若不在两侧则继续以相同的方法进行寻找，直到所有关节都找到，如果所有的摇摆关节都找完后，仍然不能够使D'的极坐标角与前一个摇摆关节的极限角分布在目标矢量角的两侧，则说明在这个矢量角下，构形平面的构形末端不能到达目标点.如果在某一摇摆关节处于极限角处，能够使D'的极坐标角与前一个摇摆关节的极限角分布在目标矢量极坐标角的两侧，则在目标矢量极坐标角处，构形平面内的构形能够达到最大的距离值.

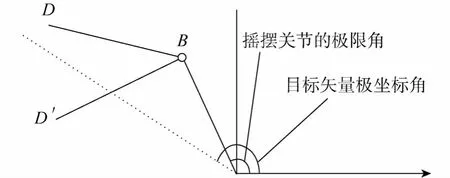
图2 最大值求解示意Fig.2 Sketch of solving the maximum value

2)极坐标角下最小值的求解.极坐标角下最小值的求解较为复杂.如果最大值存在，则最小值也就存在.

思路 首先在构形平面内找到一个摇摆中心，要求摇摆中心分成的2个部分长度的差值最小，如图3所示.然后将O2、O3为中心的摇摆模块的中心都置于极限处，察看O2O4与O3O5是否发生干涉如图4所示，对于非偏置摇摆模块，其在构形平面内是不会产生交叉状况.

图3 构形平面的摇摆中心确定示意Fig.3 Confirmation sketch of swing center of configuration plane

在△O1O2O3中，可直接求得O2O3，进而可求出∠O1O2O3和∠O1O3O2.

此时有3种情况:

1)∠O1O2O3和∠O1O3O2都没有超出摇摆关节的极限.此时O2O4与O3O5发生干涉，则最小值为0.

2)∠O1O2O3和∠O1O3O2有一个角超出了摇摆关节的极限.设∠O1O3O2超出，如图 4所示，∠O1O3O5为极限角.如果在O3O5段还有摇摆关节，则以距离O3最近的摇摆模块为中心，设为O3'.旋转该模块，使得O3'O5线段与O3'O2矢量重合.计算O2O5线段距离，判断O2O5与O2O4的2个线段大小，如果O2O5≤O2O4，则极坐标角下最小值为0;否则将O2O4旋转到O2O5矢量线上，O4O5就为极坐标角下最小值.

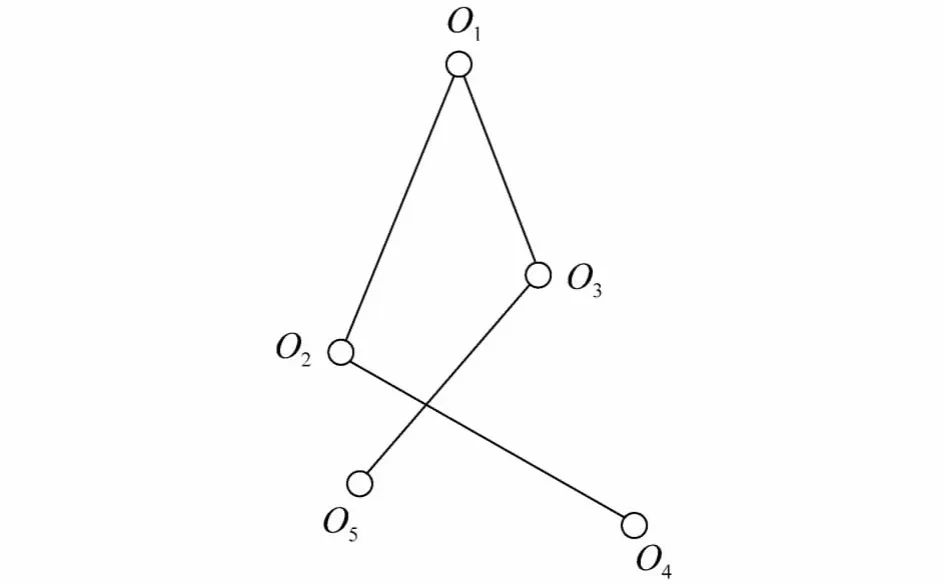
图4 最小值求解示意Fig.4 Sketch of solving the minimus value

3)∠O1O2O3和∠O1O3O2都超出了摇摆关节的极限.将这2个关节都置于极限处.其求解过程与上一种情况相同，找到O4O5的最小值.

2.3 构形平面工作空间区间的搜索

构形平面工作空间的区间搜索实际上是对区间界限的搜索.由于要兼顾精度和速度，因此搜索时采用两步搜索方法:粗搜索和精搜索结合的方法［7］.

1)粗搜索.粗搜索用于确定空间边界的大致区域，采用等步距Δl进行搜索.搜索的范围为在已知极坐标角下，通过上一节方法求的［lmin，lmax］区域.其工作流程如图5所示.

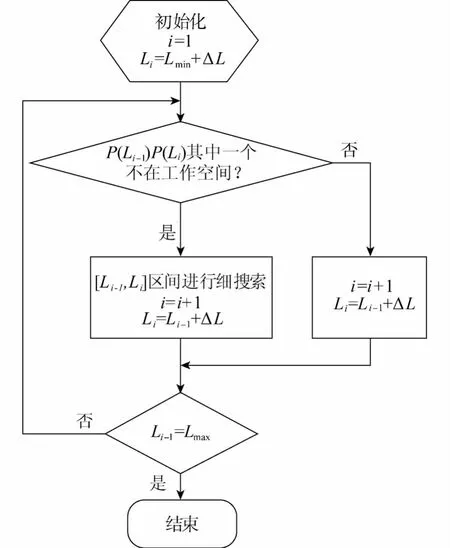
图5 粗搜索流程图Fig.5 Soarse search flowchart

2)细搜索.细搜索为通过粗搜索确定的空间边界，搜索满足一定精度的边界点，采用二分法进行边界搜索.其工作流程如图6所示.

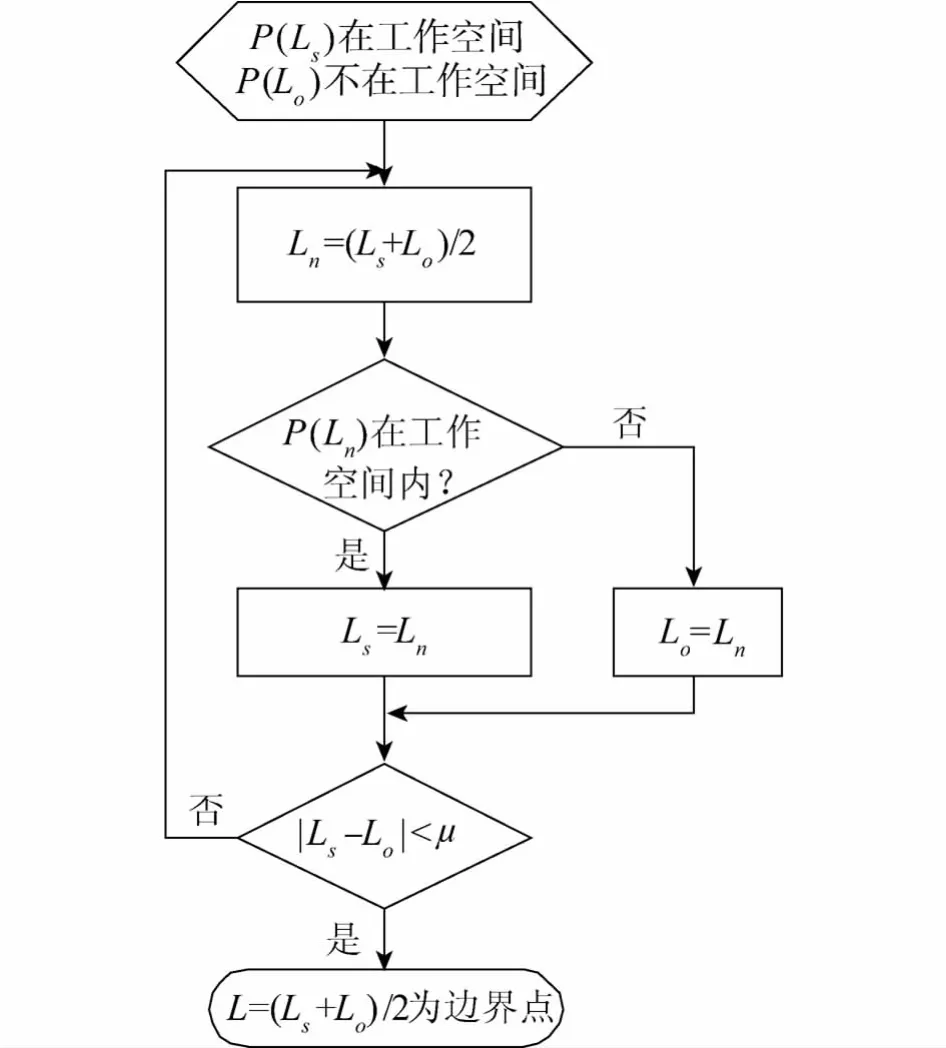
图6 细搜索流程图Fig.6 Fine search flowchart

3 8-DOF机器人的构形平面工作空间计算

以一个8-DOF机器人构形［8］进行仿真实验，其关节参数如表1所示，构形如图7所示.

表1 8-DOF机器人参数Table 1 8-DOF robot parameters

机器人初始点的位置姿态矩阵如下:

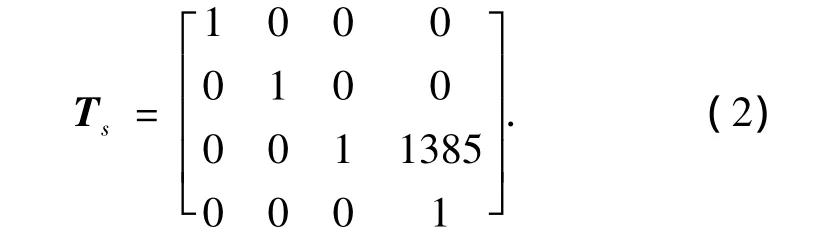
机器人运动目标点的位置姿态矩阵如下:

进行构形平面划分后，以关节2和关节7作为划分点，分解成3个构形平面:关节1与关节2组成构形平面1;关节3、关节4、关节5、关节6组成构形平面2;关节7和关节8组成构形平面3.构形平面工作空间形式固定，易于求解，也易于匹配.通过计算，构形平面2的末端相对于构形平面2的中心的位姿矩阵为

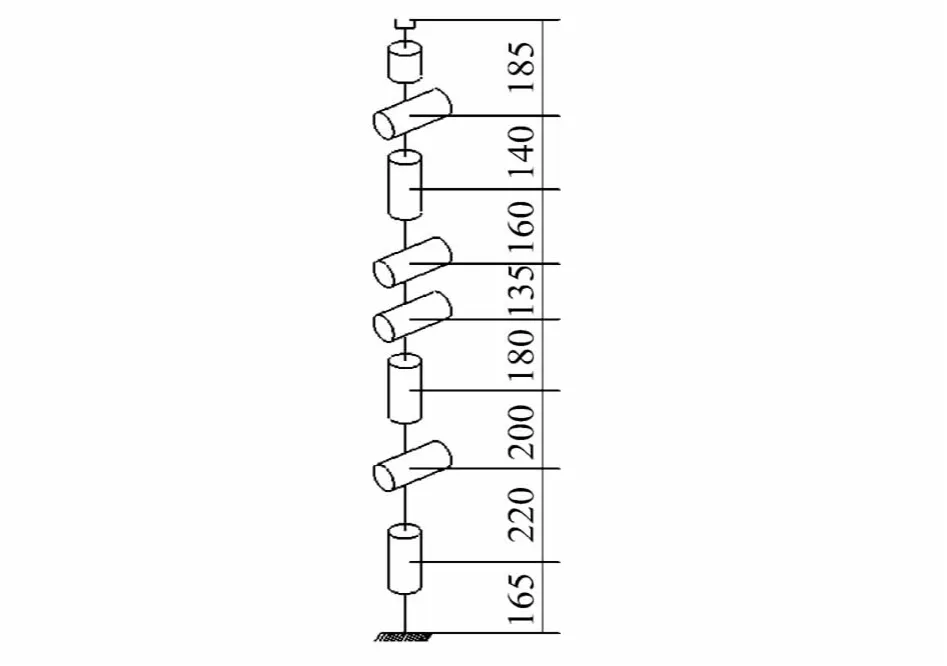
图7 8-DOF工作构形Fig.7 8-DOF configuration robot

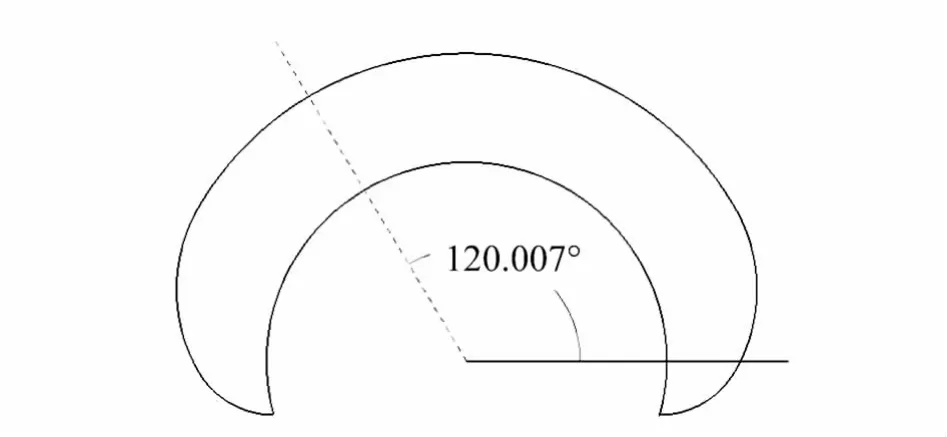
图8 极坐标下构形平面工作空间Fig.8 Configuration plane working space in polar coordinates

也就是说，在构形平面2的极坐标系中，其末端的极坐标角为120.007°情况下，极半径要满足657.5.否则，要重新划分构形平面，进行构形平面匹配.按照前面的说明，构形平面的工作空间仅是确定其在极坐标角下的工作空间内的区域.通过计算和搜索，极坐标角120.007°下，其构形平面2的工作空间为［527，815］，非多区域工作区间，如图8所示.其能够满足构形平面间的位姿匹配要求，可求出可重构机器人逆运动学解.

4 结论

1)通过对构形平面的工作空间分析，总结出4种基本构形平面的工作空间类型，为可重构机器人在任意空间工作位形下的构形平面划分提供了依据.

2)针对复杂的多连域构形平面工作空间，提出了极坐标下区间形式的工作空间表达方法，极大简化了工作空间的计算量，为可重构机器人构形平间的位姿匹配节省了时间，进而保证机器人的工作的实时性.

3)采用了先计算工作空间边界，后通过粗搜索、细搜索结合确定工作区间的方法，极大加快工作空间的计算速度，提高计算方法的效率.

［1］PAREDIS C J J，KHOSLA P K.RMMS:reconfigurable modular manipulator system project［C］//Proceedings of the 1997 IEEE International Conference on Robotics and Automation.Albuquerque，USA，1997:20-25.

［2］郑浩峻，汪劲松，李铁民.可重构机器人单元结构设计及组合特性分析［J］.机械工程学报，2003，39(7):34-37.

ZHENG Haojun，WANG Jinsong，LI Tiemin.Reconfgurable robot unit structure design and assembly character analyses［J］.Chinese Journal of Mechanical Engineering，2003，39(7):34-37.

［3］GAO Y.Decomposible closed-form inverse kinematics for reconfigurable robots using product-of-exponentials formula［D］.Singapore:Nanyang Technological University，2000: 201.

［4］CHEN Iming，GAO Yan.Closed-form inverse kinematics solver for reconfigurable robots［C］//Proceedings of the 2001 IEEE International Conference on Robotics＆Automation.Seoul，Korea，2001:2395-2400.

［5］魏延辉，赵杰，高延滨.一种可重构机器人运动学求解方法的研究［J］.哈尔滨工业大学学报，2010，42(1): 133-137.

WEI Yanhui，ZHAO Jie，GAO Yanbin.A solution method for kinematics of reconfigurable modular robots［J］.Journal of Harbin Institute of Technology，2010，42(1):133-137.

［6］WEI Yanhui，ZHAO Jie，CAI Hegao.Inverse kinematic research based on a new type of reconfigurable robot［J］.Journal of Xidian University，2008，1:175-182.

［7］赵杰，王卫忠，蔡鹤皋.可重构机器人工作空间的自动计算方法［J］.天津大学学报，2006，39(9):1082-1087

ZHAO Jie，WANG Weizhong，CAI Hegao.Algorithms for automatically determining workspace of reconfigurable robots［J］.Journal of Tianjin University，2006，39(9):1082-1087.

［8］贾庆轩，诸明，孙汉旭，等.9-DOF超冗余机器人轨迹规划优化算法［J］.北京邮电大学学报，2008，31(2):20-25.

JIA Qingxuan，CHU Ming，SUN Hanxu，et al.Research on the optimal algorithm for trajectory planning of a 9-DOF hyper-redundant robot［J］.Journal of Beijing University of Posts and Telecommunications，2008，31(2):20-25.