改进的三次相位函数法LFM雷达信号参数估计

司伟建，蒋鹏，刘旭波

(1.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001;2.中国人民解放军第91635部队，北京102249)

针对LFM信号的检测与处理方法主要有:分数阶傅里叶变换法［1］;离散匹配傅里叶变换法［2］;基于频谱细化调频信号参数估计方法［3］;基于重排小波-radon变换法［4］以及Wigner-ville变换［5］等方法.基于时频分析的方法是一类行之有效的检测方法，Wigner变换也因其对LFM信号理想的频率聚集性而被广泛应用.然而，由于受到信号交叉项的影响，并且算法计算量过大，因此并不适合于工程实现.高阶模糊函数法［6］运算速度比较快并且估计效果较好，但其算法运算时间也将近毫秒级，实时性较差.Radon-Ambiguity方法(RAT)、基于互WVD变换的检测方法、核函数优化设计法等，也是一些行之有效的LFM雷达信号参数估计方方法，但这些方法对噪声比较敏感，其多分量信号交叉项也较为严重.而小波变换等对噪声不敏感，没有交叉项的方法，其时频分辨力较低［7-12］.

学者P.O＇Shea提出了三次相位函数法.为了实现对LFM信号的参数估计，只需通过一个二阶变换，在信号参数空间寻找该变换的最大值即可估计调频斜率，由调频斜率值对原信号进行解线调，对解线调后的信号进行FFT处理即可估计信号的初始频率.

1 三次相位函数法LFM雷达信号参数估计原理

对于信号s(t)，其三次相位函数定义为

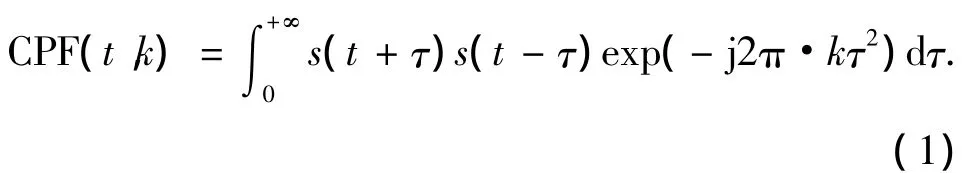
式中:k表示信号的调频斜率.

LFM信号s(t)=Aexp［j2π(at+bt2)］的三次相位函数为

式中:ζ(t)=exp［j2π·2(at+bt2)］.可见，三次相位函数必将沿着调频斜率形成最大值.

离散情况下，设信号采样点数为N，N为奇数，信号的三次相位函数表达式为

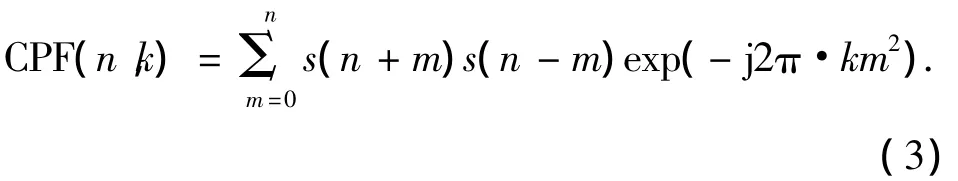
式中:n可取任意时间点.这里，n取数据中点，即n=(N－1)/2.k是搜索斜率值，算法实际操作上可先设定一个初始斜率值，以一定搜索步长对斜率k进行搜索，根据三次相位函数对应的峰值点即可估计出信号的调频斜率:

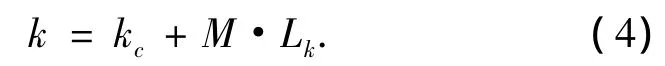
式中:kc为搜索频率初始值，M为CPF峰值点对应的频率搜索点数，Lk为搜索步进.该算法通过大范围的搜索即可估计出调频斜率，然而如果没有先验知识，算法就会进行“盲”搜索，这样势必会在远离调频斜率真实值处进行无谓的搜索而增加计算量.针对这个问题对斜率搜索范围的设定进行了探讨.

2 调频斜率搜索范围的设定

调频斜率搜索范围直接影响着算法计算量，因此提出根据信道化提取的脉冲前沿频率和脉冲宽度信息的调频斜率搜索范围判定法.在信道化中应用瞬时测频法获得频率信息，由于LFM信号瞬时相位呈非线性变化，这样测得的频率值一定会有误差，因此，所得的频率值不能当做信号的初始频率，只能当做一个参考值.由于信道化数字接收机得到的I、Q数据经过下变频以后，载频范围为0～15 MHz，假设信号调频带宽B≥2 MHz，那么，规定调频斜率k的取值规则

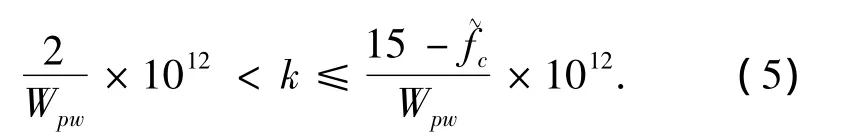
式中:频率单位为MHz，脉冲宽度单位为μs，则k的单位为Hz/s.这样，k的搜索范围是可变的.k的搜索步长可根据实际要求的精度而定，如果选定步长为Lk=2×109Hz/s，那么，k的精度为 Δk= 0.002 MHz/μs.

假设由信道化接收机测得的频率值为 fc= 3 MHz，脉冲宽度Wpw=8μs，那么，k的搜索范围为0.25×1012～1.5×1012Hz/s，根据搜索步长，总共搜索625点.

三次相位函数法通过大范围的搜索估计出调频斜率，然而如果没有先验知识，算法就会进行“盲”搜索，这样会在远离调频斜率真实值处进行无谓的搜索而增加计算量.而从式(5)可以看出，通过先验知识信号调频带宽和信道化接收机测得的频率的引入，该取值规则避免了“盲”搜索，也就是说避免了在远离调频斜率真实值处进行无谓的搜索而增加计算量的问题.由此可见，规定这样的规则可以使调频斜率的搜索范围设定更加合理，当调频斜率较小时可以避免无谓的计算量.

3 调频斜率双尺度搜索法

由粗搜索峰值点即可判断调频斜率的大致范围，然后，以峰值点对应的调频斜率值为中心，重新对该斜率附近的范围(kc+(Mc－1)·Lk1～kc+(Mc+ 1)·Lk1)进行精搜索，规定精搜索步长为 Lk2= 0.002 Hz/s.精搜索点数为2Lk1/Lk2=50.

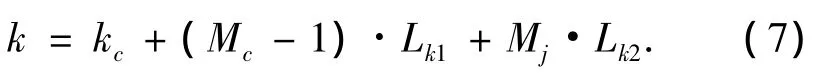
式中:kc为粗搜索初始频率，Mc为粗搜索峰值点，Mj为精搜索峰值点.

采样双尺度规则进行斜率搜索时，总共搜索

定义原算法为调频斜率单尺度搜索法，第1节提出的方法从某种程度上减小了计算量，然而，如果按照固定的步长进行调频斜率搜索，当步长设定较小时，虽然可以确保一定的精度，但计算量仍很大.针对这个问题，提出了调频斜率双尺度搜索法.

首先，以大尺度步长Lk1进行粗搜索，这里规定Lk1=0.05×1012Hz/s，由式(5)可以确定粗搜索点数: Nc+50点，而采用单一尺度进行斜率搜索时，需要进行Nd点搜索，其中Nd由下式确定:

当估计出调频斜率之后对原信号进行解线调处理，假设斜率估计值为，那么解线调后的信号表达式为

由上式可知，解线调后的信号相当于带宽非常窄的线性调频信号，如果调频斜率估计值精度很高，那么，解线调后的信号近似一个单载频信号，对处理后的信号进行FFT处理即可估计出信号初始频率.

综上所述，改进后的CPF算法估计LFM信号参数步骤为

1)由信道化过程对信号进行信号脉冲宽度提取，同时进行信号初始频率粗测量，以此设定调频斜率搜索范围;

2)设定算法时间点，对于LFM信号一般取脉冲中心位置作为时间点，同时设定数据滑动点数;

3)应用双尺度搜索法进行调频斜率估计;

4)由估计出的调频斜率值对信号进行解线调;

5)对解线调后的信号进行FFT处理，求出信号的初始频率.

4 CPF估计LFM信号仿真测试

实验1 单尺度搜索法测试实验，参数:LFM信号表达式 s(t)=Aexp［j2π(at+bt2)］，信噪比SNR=0 dB，a=3 MHz，b=4.23×1011，脉冲宽度10－5s，fs=60 MHz.

将时间点取在整个采样序列的中点，n=300，按照离散CPF计算公式，设定数据滑动点数，此处取300点，即每进行一次搜索要做300次乘累加.由信道化输出的频率，脉冲宽度Wpw=10 μs.那么，调频斜率k的搜索范围为0.2×1012～1.1× 1012，以固定步长2.0×109进行频率搜索，那么，整个区间的搜索点数为450点.以搜索点数为横坐标，CPF幅度为纵坐标，输出结果如图1.

图1为信噪比等于0 dB时的三次相位函数结果，根据峰值点对应的横坐标位置计算调频斜率值，图中峰值出现在第322点，调频斜率值为0.846× 1012，估计误差为0.

图1 单尺度下LFM信号的CPF估计结果Fig.1 The single-scale estimation of LFM based on CPF

实验2 双尺度搜索法测试实验，参数与实验1设置相同，首先进行斜率粗搜索，如图2.

经检测得到粗检测CPF峰值出现在第13点，此时估计的调频斜率值为 0.85×1012，误差为0.5%，如果用此斜率值对原信号进行解线调，得到的解线调信号将是一个窄带LFM信号，而且带宽随着调频斜率估计误差增大而变宽，这样就会严重影响信号初始频率的估计.

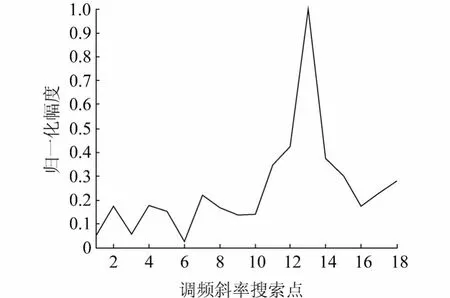
图2 双尺度下调频斜率粗搜索估计结果Fig.2 The frequency slope rough search under dual scales

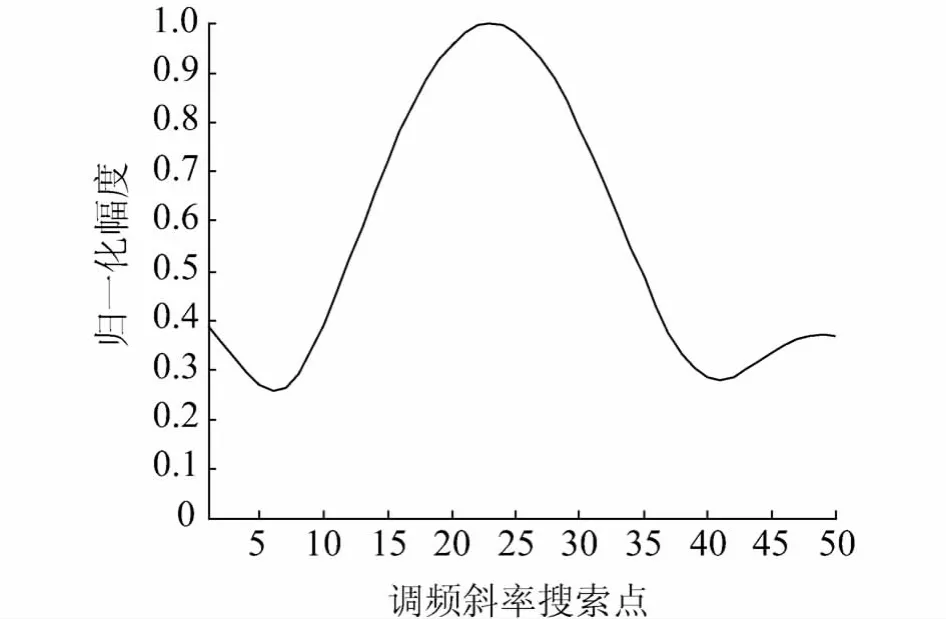
图3 双尺度下调频斜率精搜索估计结果Fig.3 The frequency slope accurate search under dual scales

下面以0.8×1012为初始值，对频率进行精搜索，结果如图3.经检测得到精检测CPF峰值出现在第23点，此时估计的调频斜率误差为0.由估计出的斜率值对原信号进行解线调.估计误差受2个因素影响:1)调频斜率搜索步长精度;2)信号采样频率与FFT点数.

下面考察一下该算法的抗噪性，在不同信噪比下进行100次Monte-Carlo实验，正确检测概率随信噪比变化曲线如图4.从图中可以看出，当SNR＞－8dB时CPF算法正确检测概率超过90%.因此，虽然CPF算法计算量较大，但其抗噪性是十分优良的.

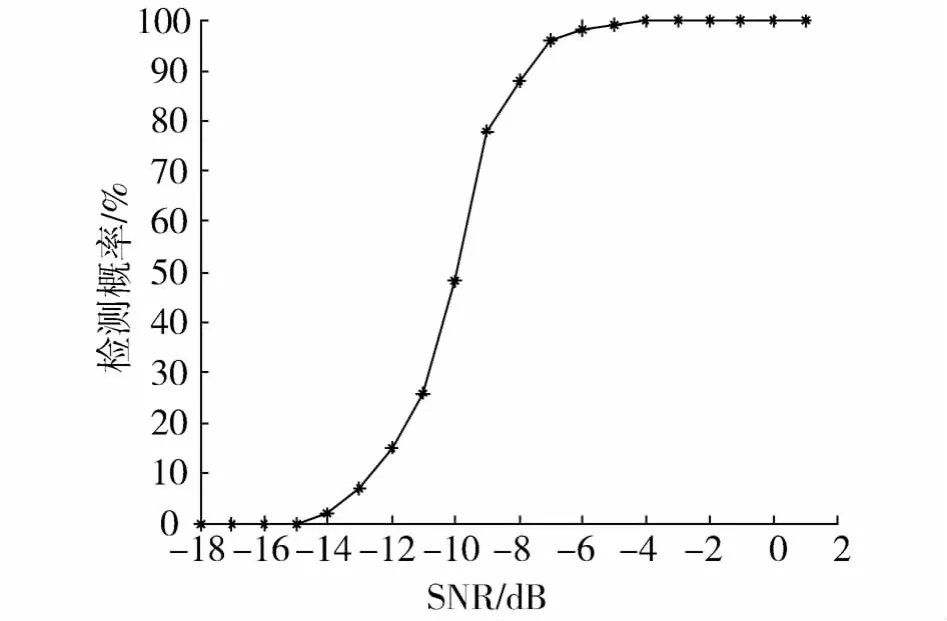
图4 不同信噪比下CPF算法正确检测峰值概率统计Fig.4 The correct peak points detection probability statistics of CPF algorithm in different SNR

5 结束语

针对LFM信号参数估计问题，采用了三次相位函数法作为基础来估计信号相位多项式系数，文中提出了该算法频率搜索范围设定方法，并针对CPF算法计算量大的问题，提出了双尺度调频斜率搜索法，从仿真结果里可以看出，该方法很大程度上减少了计算量，同时保证了在低信噪比下的算法精度，使算法的性能得到了提升.为了减少计算量，必然导致搜索步长精度的下降，对于这对相互矛盾的问题，则需要根据不同的精度要求进行取舍，选取恰当的折中值.该改进算法减少计算量的能力，可以缩短系统运算时间，为硬件及工程实现提供了方便，以达到更好的实时性要求.

［1］AKAY O，BOUDREAUX-BARTELS G F.Fractional convolution and correlation via operator methods and an application to detection of linear FM signals［J］.IEEE Transactions on Signal Processing，2001，49(5):979-993.

［2］安伟刚，程少云.基于DMFT的LFM信号参数估计［J］.现代电子技术，2009，32(1):1-3.

AN Weigang，CHENG Shaoyun.LFM signal parameter estimation based on discret match Fourier transform［J］.Modern Electronics Technique，2009，32(1):1-3.

［3］司锡才，朱晓.基于频谱细化的线性调频信号参数估计［J］.系统工程与电子技术，2009，31(3):507-510.

SI Xicai，ZHU Xiao.LFM signal parameter estimation based on spectrum zoom［J］.Systems Engineering and Electronics，2009，31(3):507-510.

［4］李利，司锡才，柴娟芳，等.基于重排小波-Radon变换的LFM雷达信号参数估计［J］.系统工程与电子技术，2009，31(1):74-77.

LI Li，SI Xicai，CHAI Juanfang，et al.Parameters estimation for LFM radar signal based on reassigned wavelet-Radon transform［J］.Systems Engineering and Electronics，2009，31(1):74-77.

［5］孙泓波，顾红.基于互Wigner-Ville分布的SAR运动目标检测［J］.电子学报，2002，30(3):347-350.

SUN Hongbo，GU Hong.SAR moving targets detection based on cross Wigner-Ville distribution［J］.Acta Electronica Sinica，2002，30(3):347-350.

［6］BARBAROSSA S，SCAGLIONE A，GIANNAKIS G B.Product high-order ambiguity function for multicomponent polynomial phase signal modeling［J］.IEEE Trans Signal Processing，1998，46(3):691-708.

［7］肖慧.LFMCW雷达高速/加速目标参数估计及测距范围扩展技术研究［D］.长沙:国防科技大学，2008:50-88.

XIAO Hui.Research on processing techniques of highspeed/accelerating targets and detectable range extension based on LFMCW radar［D］.Changsha:National University of Denfense Technology，2008:50-88.

［8］池庆玺.脉压雷达脉内特征分析与处理技术研究［D］.哈尔滨:哈尔滨工程大学，2007:79-111.

CHI Qingxi.Research of pulse compression radar signal intra-pulse feature analysis and processing technology［D］.Harbin:Harbin Engineering University，2007:79-111.

［9］沈海华.复合调制雷达信号识别和处理方法的研究［D］.南京:南京航空航天大学，2008:31-53.

SHEN Haihua.Research on the identification and the treatment of the composite modulation radar signal［D］.Nanjing: Nanjing University of Aeronautics and Astronautics，2008:31-53.

［10］文海.雷达脉压信号脉内特征分析研究［D］.哈尔滨:哈尔滨工程大学，2006:38-65.

WEN Hai.The research of radar pulse compression signal intra-pulse modulation characteristics analysis［D］.Harbin:Harbin Engineering University，2006:38-65.

［11］周违.空间信号检测与参数估计算法研究［D］.西安:西安电子科技大学，2006:25-48.

ZHOU Wei.Study on algorithms for spatial signal detection and parameters estimation［D］.Xi`an:Xidian University，2006:25-48.

［12］邓振淼.雷达信号脉内分析与处理理论及算法研究［D］.南京:南京航空航天大学，2007:66-86.

DENG Zhenmiao.Study on theories and algorithms of intrapulse analysis and processing of radar signals［D］.Nanjing:Nanjing University of Aeronautics and Astronautics，2007:66-86.