圆柱体出筒过程头型对流体动力的影响

刘海军，王聪，邹振祝，王本利，王柏秋

(1.哈尔滨工业大学航天学院，黑龙江哈尔滨150001;2.河北大学建筑工程学院，河北保定071002)

圆柱体的出筒方式，可分为有动力和无动力出筒.根据布置方式可分为垂直、水平和倾斜出筒;根据筒内圆柱体周围的环境分为干式和湿式出筒，等［1］.无论采用哪种方式，圆柱体都要经历出筒、水中航行、出水和空中飞行4个阶段，尽管前3个阶段的运动距离和时间比较短，但会形成复杂多相流场，对圆柱体的流体动力、弹道等产生直接影响，从而影响圆柱体运动的稳定性［2］.

圆柱体在水下运动的时间很短，却存在复杂的流场情况.Jon J.Yagla等［3］对水下垂直发射系统的动力环境进行了研究，提出了筒内发动机点火的方式发射导弹，可以为导弹出水提供一个从出筒到出水整个过程的气幕，并进行了相关的实验研究.Chris J.Weiland等研究了不同发射深度和横向流对垂直发射导弹的弹道的影响［4］.殷崇一等运用有限体积法和SIMPLE算法计算了导弹水下发射内流场的数值研究［5］.刘乐华等采用TVD有限体积法，对导弹水下大深度发射内流场进行了数值模拟，研究流场波系结构、压力、温度等参数随时间变化的规律［6］.朱明骏等对潜射导弹的充气均压系统进行了研究，利用 PID控制方法对充压系统进行了设计［7］.王汉平等采用多相流模型和动网格技术研究了均压气体对弹射后效的影响［8］.刘筠乔等研究了导弹垂直发射出筒过程的通气空泡流［9］.张红军等对不带空化模型的潜射导弹垂直出筒过程进行了研究［10］.

国内外主要对圆柱体外流场进行了研究，而对出筒过程中内弹道和流体动力特性的研究相对较少.本文采用动网格技术，并结合求解考虑质量输运空化模型的混合介质的RANS方程，实现了重力影响下的圆柱体边界运动与气(汽)水流场的耦合求解，针对采用筒内点火的方式对圆柱体出筒过程的多相流场进行了数值模拟，研究了重力影响下的3种头型的圆柱体出筒过程和流体动力特性.

1 圆柱体出筒过程数学模型

1.1 流体控制方程

描述水下圆柱体出筒过程的控制方程主要包括混合物的连续方程、动量方程、能量方程、湍流模型和空化模型.

混合物连续性方程:

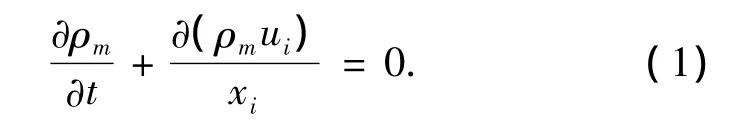
式中:ui为i方向的速度分量;ρm为混合物的密度，ρm=αlρl+αvρv+αngρng，ρi和αi(i=l，v，ng)，分别为水、水蒸气及不可凝结气体的密度和体积分数.

混合物动量方程:

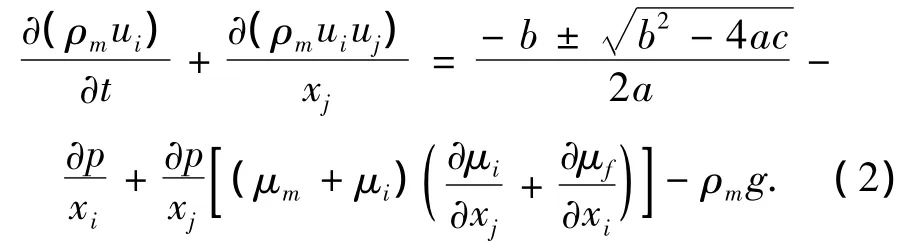
1.2 湍流模型

标准的k－ε湍流模型:

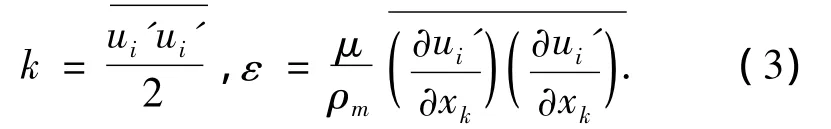
湍动能k和湍动耗散率ε的输运方程如下:

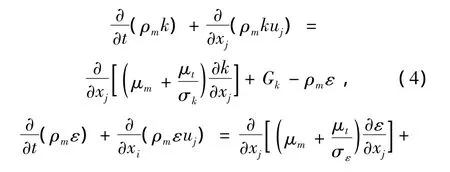
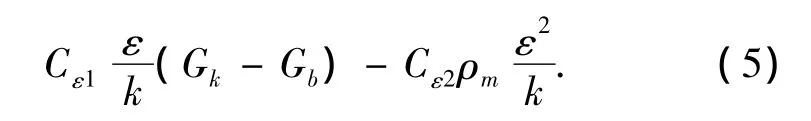
式中:k和ε分别为湍动能和耗散率，Gb由浮力引起的湍动能k的产生项，Gk为由平均速度梯度引起的湍动能k的产生项，μt为湍流粘性系数，σk和σε分别为k和ε的普朗特数.5个经验常数取值分别为:Cε1= 1.44，Cε2=1.92，σk=1.0，σε=1.3，Cμ=0.09.

1.3 空化模型

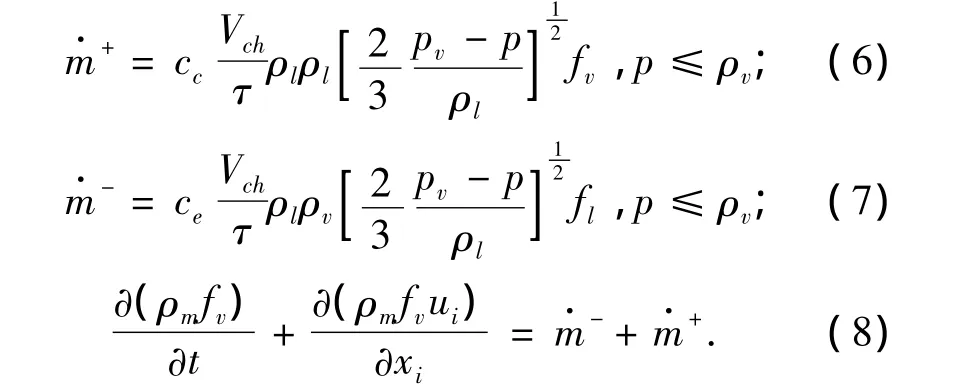
式中:Vch为特征速度，表示当地液相和汽相之间的相对速度，本文中取，其中k为当地湍动能;τ为表面张力系数;pv为指定温度下水的饱和蒸汽压力，经验常数: Cc=0.01，Ce=0.02，f1=1－fv－fng，其中不可凝结气体分数fng=1.5×10－5，fi=αiρi/ρm(i=l，v，ng)为各相的质量分数，不可凝结气体定义为理想气体;m·－和m·+分别表征汽化和液化过程的源相.

1.4 能量方程

能量方程为

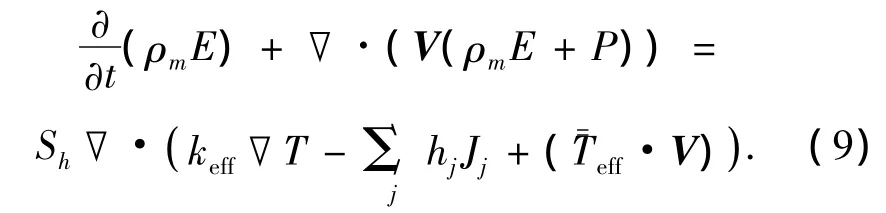
式中:keff为传导率，keff=(k+kt)，kt为湍流的热传导率;J为物质j的扩散通量;Sh为一切热源.方程(9)右边的后3项分别代表由热传导、物质扩散和粘性耗散引起的能量交换.

其中，h为焓，理想气体的焓为

不可压缩流体的焓为

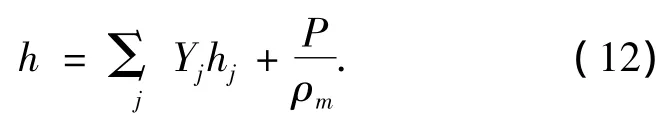
式中:Yj为物质j的质量分数，

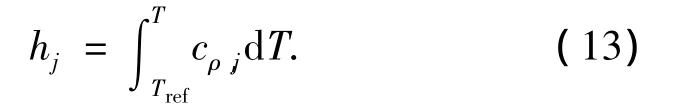
1.5 圆柱体的运动方程

假定水下圆柱体为刚体，由牛顿第二定律计算圆柱的运动，圆柱体边界运动方程采用如下离散形式:

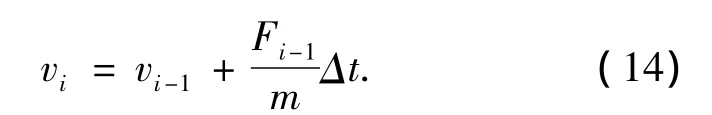
式中:vi和vi－1分别代表第i和i－1个时间步圆柱体的运动速度，Δt为时间步长，Fi－1为第i－1个时间步圆柱体所受的合力，m为圆柱体的质量.合力由下公式算得

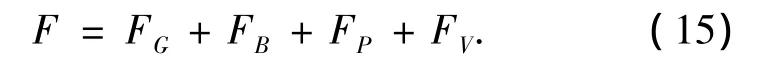
式中:FG为圆柱体受到的重力，FB为圆柱体的底部受到的推力，FG和FB由初始条件给出，FP为圆柱体受到的压差阻力，FV为圆柱受到的粘性阻力，FP和FV从非稳态流场计算得出.

2 数值仿真方法

采用有限体积法对控制方程进行离散，利用Simple方法求解混合介质RANS方程，采用二阶迎风格式对动量方程、对流项和湍流耗散项进行离散，采用PRESTO!对压力项进行离散.利用FLUENT中的自定义函数(UDF)和动网格技术，求解圆柱体出筒过程中的运动速度及位移.

数值方法正确性验证，将半球头型弹体的仿真结果与已有的实验数据进行对比，验证了数值求解方法的正确性.验证算例采用模型为:半球头型弹体直径为50 mm、总长度为200 mm.计算条件是:未受扰动水流场压强p∞=378 955 Pa，采用非定常过程计算.以弹体直径D计算雷诺数为Re=106，空化数σ=0.31，图1是圆柱体表面压力分布与实验数据对比曲线.H为距离弹头顶点处的轴向距离，从图中看出仿真结果和实验数据吻合较好.因此，采用动态分层方法的动网格技术，结合求解混合介质RANS方程，可以实现弹体边界运动与汽水流场的耦合求解，并以此为基础对潜射圆柱体垂直出筒过程空化多相流场开展数值研究.

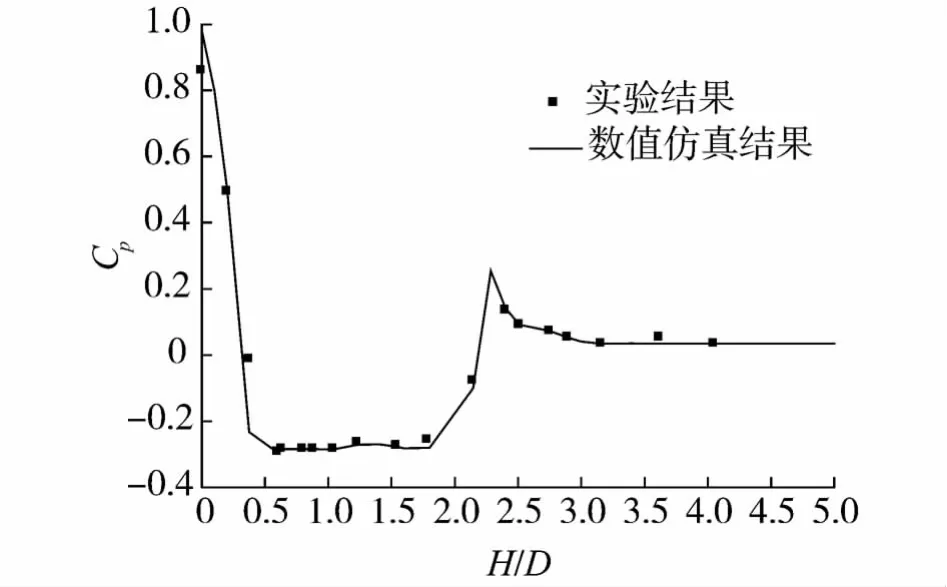
图1 数值模拟结果验证Fig.1 Validity of numerical simulation results

3 计算模型及边界条件

图2是圆柱体出筒过程示意图，整个计算区域分为2块:中间为动网格区域，周围为静网格区域.

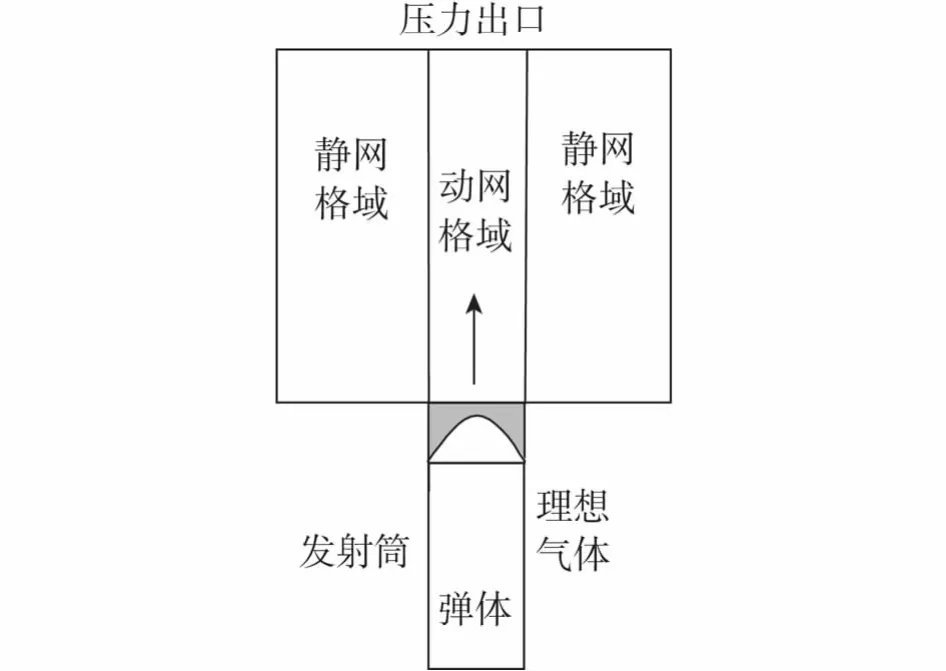
图2 计算区域与模型Fig.2 Computional zone and model

圆柱体的长细比L/D=10，L为圆柱体的长度，D为圆柱体的直径，水深为50 m.计算域由筒内的气体和筒外的水域组成.图2给出了流场计算区域、网格和边界条件的示意图，在圆柱体头部附近的网格进行了加密处理.流场的长度是50D，宽度是12D.圆柱体喷管入口是本模型的压力入口.

图3 计算区域与网格Fig.3 Computational domain and grid

图4是总压曲线，特征时间T=L/Vmax给出，式中Vmax为出筒的最大速度，Pmax为最大压力值.

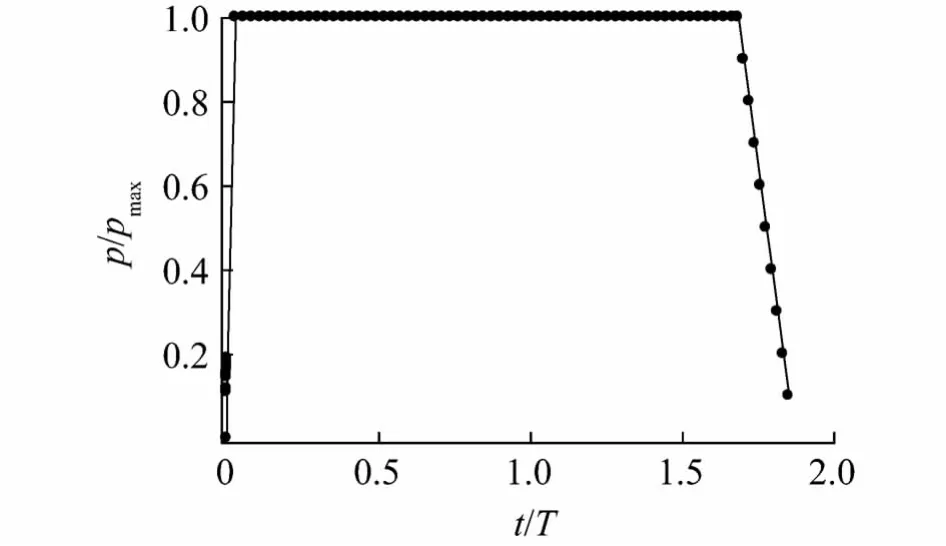
图4 燃气总压随时间变化的曲线Fig.4 Toll pressure of gas versus time

4 计算结果及分析

对3种头型的圆柱体出筒过程中的流场、表面压力、水下弹道和水下流体动力进行计算及分析.

4.1 圆柱体出筒过程流场分析

水下圆柱体运动产生空化的判据用无量纲的量空化数σ来表示，其表达式为，式中v为圆柱体的速度，p∞为未扰动流场的压力，pv为饱和蒸汽的压力，ρ为水的密度.图5是圆柱体空化云图，模型Ⅰ是小钝角头型，模型III是大钝角头型.模型III肩部空泡最大，模型Ⅰ肩空泡最小.

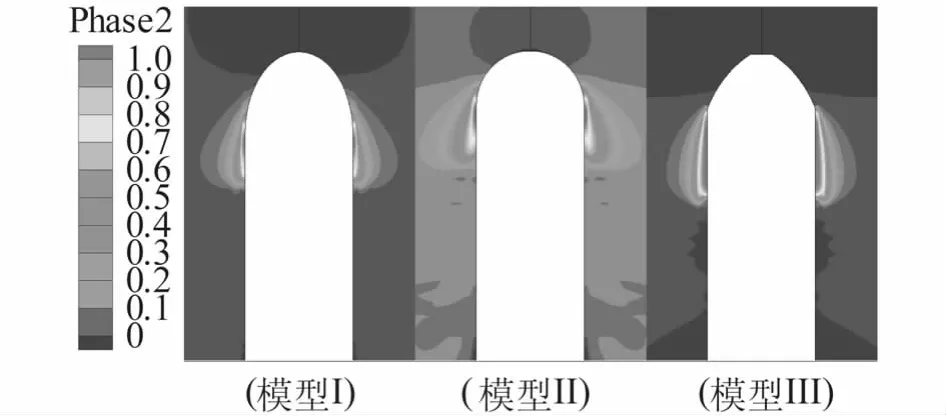
图5 不同结构圆柱体的空化云图Fig.5 Contours of cavitation to different structare cylinder

图6是气相体积分数和汽相体积分数的变化曲线，3种头型的气相体积分数曲线，t/T≤1，都平行于轴线且几乎重合，t/T≥1，模型Ⅲ的下降速度最快，模型I则最慢.

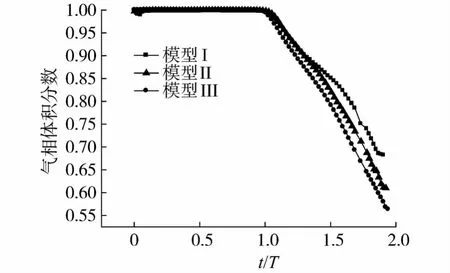
图6 气相体积分数的变化Fig.6 Gas volume fraction versus time

图7是汽相体积分数曲线，在t/T≤1时，都平行于轴线且接近0，t/T≥1，模型III的增加速度最快，模型Ⅰ则最慢.在圆柱体头部由运动产生的动压较大，不满足空化的条件，故没有出现空化现象，在大钝角头型的圆柱体的肩部因液体的绕流较容易产生低压区，满足了变化空化的条件，故模型III的肩部空化就容易产生.

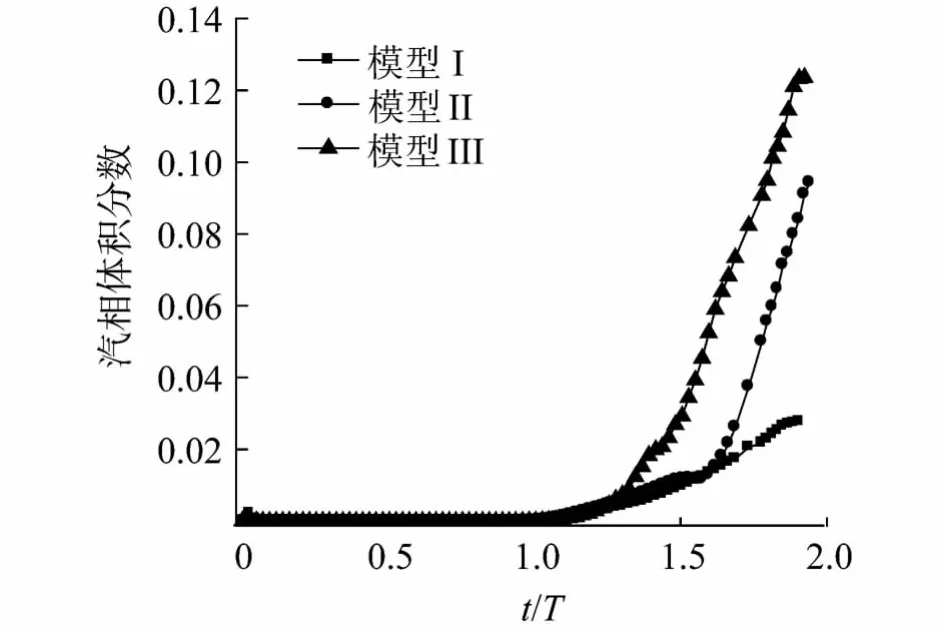
图7 汽相体积分数的变化Fig.7 Volume fraction of vapor versus time

4.2 圆柱体表面压力分析

图8是圆柱体出筒时的表面压力比值的分布曲线，左侧是圆柱体头部，右侧是圆柱体尾部，h为距离圆柱体头部的距离.模型III的肩部出现的绕流低压区最大，模型Ⅰ则最小;在圆柱体的中段，模型I的压力最大，模型III的压力最小;在圆柱体的尾部，模型I的压力最大，模型III则最小，3种头型都有小幅波动，在出筒时刻，圆柱体的尾部还在发射筒口的高压气体之中，气团的膨胀和收缩是波动的原因.

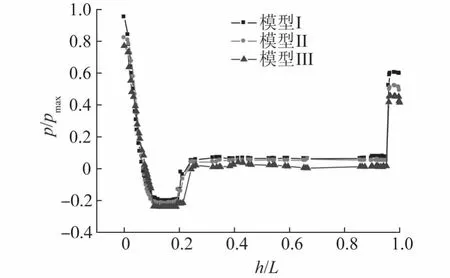
图8 圆柱体表面环向压力比值沿轴向分布Fig.8 Cylinder surface pressure ratio along axis

4.3 圆柱体出筒弹道分析

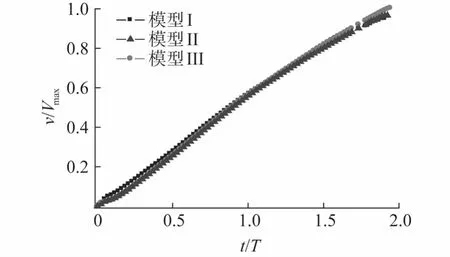
图9 圆柱体速度变化曲线Fig.9 Cylinder velocity versus time

图9是圆柱体速度变化曲线，从图中可以看出，模型III的速度最大，模型Ⅰ最小，这是由于航行体出筒过程中模型III的肩部空化最大，圆柱体的沾湿面积最小，摩擦阻力最小，所以速度最大.

图10是位移变化曲线，从图中看出，模型III的位移最大，模型Ⅰ则最小，这是由于相同时间内速度越大圆柱体上升的位移越大，模型III的速度最大，故模型III的位移最大.

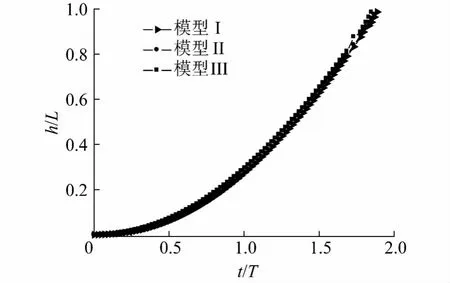
图10 圆柱体位移变化曲线Fig.10 Cylinder displacement versus time

图11 圆柱体加速度变化曲线Fig.11 Cylinder acceleration versus time

图11是加速度变化曲线，模型III的加速度最大，模型I则最小，3种头型的加速度在初始刻的波动是由于发动机的推力逐渐达到峰值和气团的膨胀和收缩的原因，随着时间的推移3种头型的加速度抖动下降，模型III的波动最小，模型I则最大.故模型III的水下弹道变化较小且比较稳定，模型I的弹道变化较大稳定性较差.通过增加头型的角度可以得到较理想的弹道，为工程应用提供了理论参考.

4.4 圆柱体出筒过程受力分析

图12～14分别是压差系数、粘性系数和总动力系数的变化曲线.圆柱体运动方向为坐标轴x的正向，力的系数用公式Cx=Fx/(0.5ρV2S)给出，式中ρ为水的密度;V为圆柱体的速度;S为圆柱体的横截面面积;Fx=Fp+Fd，Fp为推力，Fd为阻力，Fd= fg+fw，fg为空气的粘性力，fw为水的粘性力.出筒过程中的压差力、粘性力和总动力都为正值.图12是压差系数变化曲线，在初始刻有波动，曲线下降且趋缓，模型III的压差力最大而且波动较小，模型Ⅰ的压差力则最小而且波动较大.

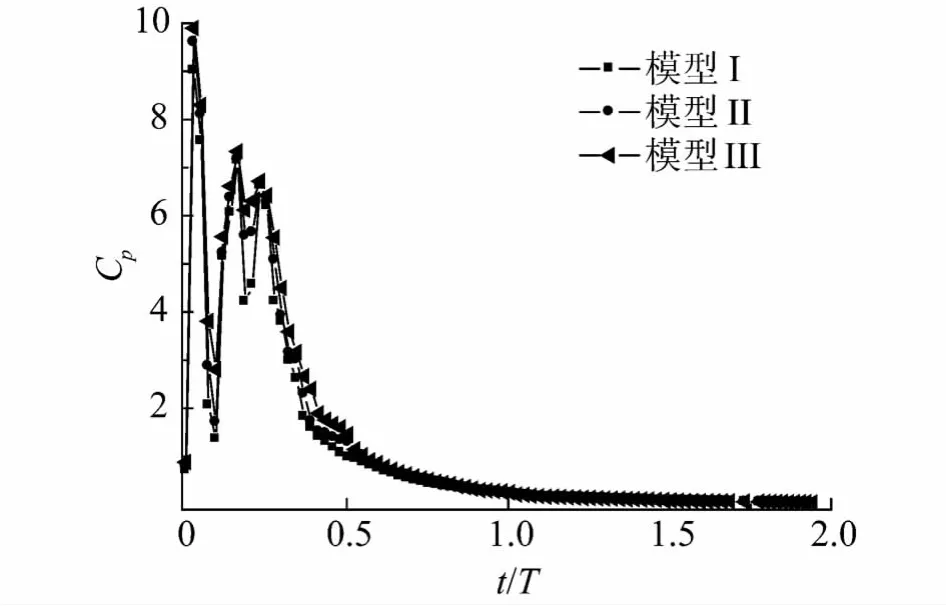
图12 圆柱体压差系数变化曲线Fig.12 Cylinder pressure coefficient versus time

圆柱体的粘性力系数的变化规律，见图13，从图中看出，3种头型圆柱体的粘性力都有相同的波动然后下降且趋缓，模型III的粘性摩擦力最小而且波动较小，模型I粘性摩擦力较大而且波动较大，肩部空泡的出现增大了圆柱体的压差阻力系数，减小了粘性摩擦阻力系数.

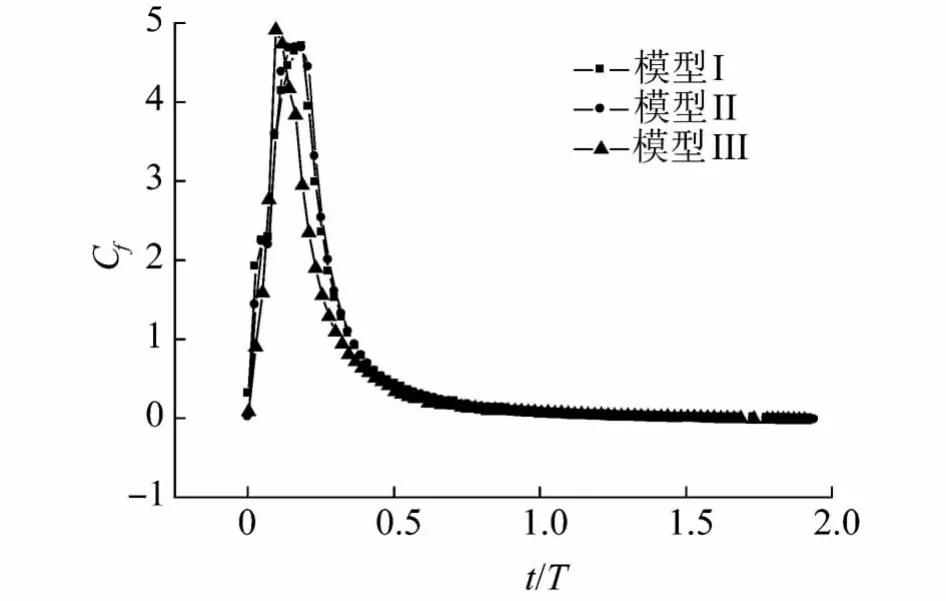
图13 圆柱体摩擦系数变化曲线Fig.13 Cylinder friction coefficient versus time

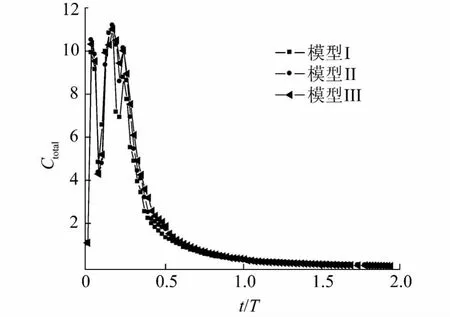
图14 圆柱体总流体动力系数变化曲线Fig.14 Cylinder toll hydrodynamic coefficient versus time

圆柱体总流体动力系数变化规律，见图14，从图中可以看出，模型III的总流体动力系数最大而且波动较小，模型I的总流体动力则最小且波动较大.由于模型III的总流体动力系数的波动较小，对圆柱体水下弹道稳定的影响较小.压差力、粘性摩擦力和总流体动力系数出现的波动都是由发动机的推力逐渐增加到峰值和气团出筒时的膨胀和收缩导致.

5 结论

本文基于混合多相流模型，采用k-ε湍流模型，Singhal空化模型和动网格技术，结合求解考虑质量输运空化模型的混合介质RANS方程，实现了圆柱体边界运动与气水流场的问题的求解.并对重力影响下的不同头型的水下圆柱体出筒过程进行了数值仿真研究，得到的主要结论如下:

1)在出筒的过程中模型III比模型II和模型Ⅰ产生空化较早并且形成肩部空泡最大，大钝角易发生空化，则小钝角不易发生空化.

2)在出筒过程中模型III的位移、速度和加速度比模型II和模型Ⅰ都大而且波动较小;模型III出筒过程中水弹道比较稳定.

3)模型III流体动力较大而且波动较小，模型Ⅰ流体动力较小而且波动较大.模型III出筒过程中流体动力对其水弹道的稳定影响较小.

［1］颜开，王宝寿.出水空泡流动的一些研究进展［C］//第二十一届全国水动力学研讨会暨第八届全国水动力学学术会议赞两岸船舶与海洋工程水动力学研讨会文集.济南，中国，2008.

YAN Kai，WANG Baoshou.Some of research progress of water-exit cavity［C］//Proceedings of the 21st National Conference on Hydrodynamics and 8th National Congress on Hydrodynamics and the Cross-Strait Conference on Ship and Ocean Engineering Hydrodynamics.Jinan，China，2008.

［2］黄寿康.流体动力·弹道·载荷·环境［M］.北京:宇航出版社，1991:165-180.

［3］YAGLA J J.Launch dynamics environment of a water piercing missile launcher［C］//24th International Symposium on Ballistics.New Orleans，2008.

［4］PAVLOS W，YAGLA J J.Concept analysis and laboratory observations on a water piercing missile launcher［J］.O-cean Engineering，2010，3(9):959-965.

［5］殷崇一，张宇文，刘乐华，等.导弹水下发射内流场的数值研究［J］.弹箭与制导学报，2003，23(3):56-58.

YIN Chongyi，ZHANG Yuwen，LIU Lehua，et al.A numerical study of the interior flow for underwater launched missile［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2003，23(3):56-58.

［6］刘乐华，张宇文，袁绪龙.水下大深度垂直发射内流场的数值研究［J］.水动力学研究与进展:A辑，2005，20 (1):90-94.

LIU Lehua，ZHANG Yuwen，YUAN Xulong.Numerical simulation of the interior flow for launch under deep water［J］.Journal of Hydrodynamics:Ser A，2005，20(1):90-94.

［7］朱明骏，杨军.潜射导弹充气均压系统建模与控制系统设计［J］.战术导弹控制技术，2010，27(1):26-30.

ZHU Mingjun，YANG Jun.Modeling and design of pressure servo system used in underwater launched missile［J］.Control Techonology of Tactical Missile，2010，27(1):26-30.

［8］王汉平，吴友生，程栋，等.潜射模拟弹弹射后效分析［J］.船舶力学，2010，14(10):1122-1128.

WANG Hanping，WU Yousheng，CHENG Dong，et al.Analysis of ejection after-effect for underwater-launched emulating missile［J］.Journal of Ship Mechanics，2010，14 (10):1112-1128.

［9］刘筠乔，鲁传敬，李杰，等.导弹垂直发射出筒过程通气空泡流研究［J］.水动力学研究与进展:A辑，2007，22 (5):549-554.

LIU Yunqiao，LU Chuanjing，LI Jie，et al.An investigation of ventilated cavitating flow in vertical launching of a missile［J］.Chinese Journal of Hydrodynamics:Ser A，2007，22 (5):549-554.

［10］张红军，陆宏志.潜射导弹出筒过程三维非定常数值模拟研究［J］.水动力学研究与进展:A辑，2010，25(3): 405-415.

ZHANG Hongjun，LU Hongzhi.Numerical investigation to vertical launching of submarine launching missile［J］.Chinese Journal of Hydrodynamics:Ser A，2010，25(3): 405-415.