双锥面二次包络环面蜗杆传动多目标优化设计

邱清盈，舒勤业，冯培恩，朱肖虎，曹磊

(浙江大学机械工程学系，浙江杭州310027)

环面蜗杆副传动相对于普通圆柱蜗杆传动，具有同时啮合齿数多、啮合时呈双线接触、接触点的法向速度大、综合曲率半径大、接触应力小、易形成油膜等优点，因此具有更高的传动效率和承载能力，更长的使用寿命.环面蜗杆副传动在冶金、采矿、军工、化工、造船等领域已得到了广泛的应用.环面蜗杆按产型面的不同可分为直廓环面蜗杆、平面包络环面蜗杆、锥面包络环面蜗杆以及双锥面包络环面蜗杆，根据是否以一次包络所得的滚刀产型面来加工蜗轮又可分为一次和二次包络环面蜗杆传动.

国内外学者针对各种类型的蜗杆传动副，在模型建立、啮合性能分析、加工修型、优化设计等各方面开展了长期的研究［1-4］.在环面蜗杆副的优化设计方面，学者也做了相关的研究［5-9］，建立了各种不同类型，不同优化目标的优化设计模型.

双锥面二次包络环面蜗杆传动不仅具有环面蜗杆副的承载能力大、传动效率高及使用寿命长的优点，而且不易引起蜗杆边齿顶变尖和根切等加工问题.在加工时，由于其左右侧齿面同时进行磨削，在生产效率方面也有很大的优势.但国内外针对双锥面二次包络环面蜗杆副的研究却较少.本文以双锥面二次包络环面蜗杆作为研究对象，结合自主研发的加工和检测设备，对该种环面蜗杆传动进行多目标优化设计，以期获得一种比较通用的设计方法，使双锥面二次包络环面蜗杆副达到更优的性能.

1 双锥面二次包络环面蜗杆副模型

选择如图1所示的坐标系，建立蜗杆副的数学模型.其中σo1(O1;io1，jo1，ko1)为蜗杆静坐标系，σo2(O2;io2，jo2，ko2)为蜗轮静坐标系，σod(Od;iod，jod，kod)为刀座静坐标系.σo1、σo2、σod均与机架固连.σ1(O1;i1，j1，k1)、σ2(O2;i2，j2，k2)、σd(Od;id，jd，kd)分别与蜗杆、蜗轮、刀座固连.k1=ko1，k2=ko2，kd= kod.蜗杆转角为φ1，蜗轮转角为φ2，φ2=i21φ1，i21为蜗轮蜗杆的传动比，初始位置φ1=φ2=0°，σ1与σo1重合，σ2与σo2重合.刀座转角为φd，蜗杆毛坯转角为φ，φd=id1φ，id1为刀座与蜗杆毛坯的速比，初始位置φ=φd=0°，σd与σod重合.

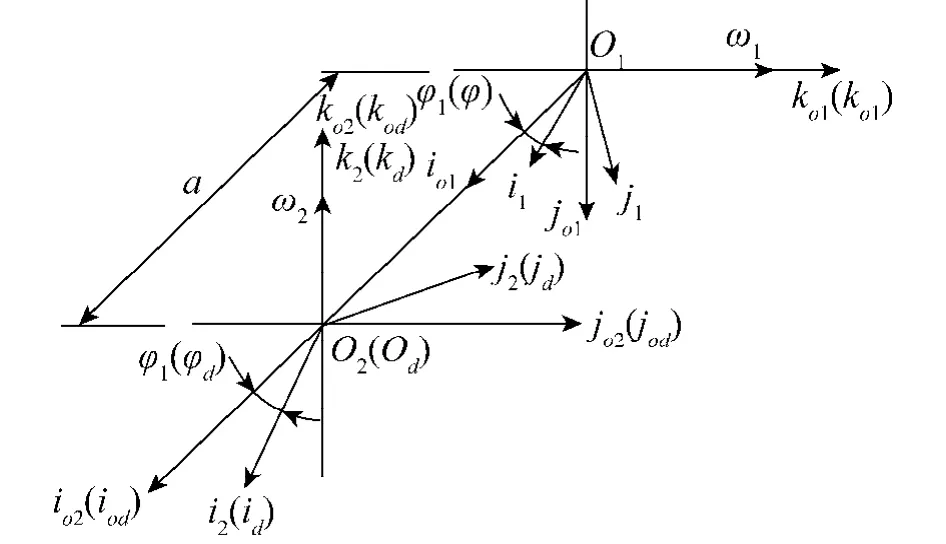
图1 双锥面二次包络环面蜗杆副的坐标系Fig.1 Coordinate system for dual-cone double enveloping hourglass worm gear pair

如图2所示，砂轮的齿形角为αd，齿顶宽为sa.取坐标系σa(Oa;ia，ja，ka)与砂轮固连.产形双锥面Σd在σa里的方程为

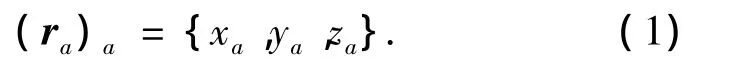
式中:xa=－ucosαdcos θ+rdcos θ，ya=－ucosαdsin θ+ rdsin θ，za=±(usinαd+0.5sa).

式中:za取正，表示砂轮右侧;za取负，表示砂轮左侧.

在Σd任一点Q处的切平面上建立活动坐标系σd(Q;αξ，aη，n).对式(1)进行σa→σd坐标变换，可得到产形双锥面Σd在σd里的方程:

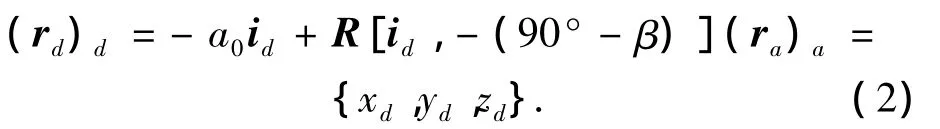
式中:R［id，－(90°－β)］的意义是表示矢量绕id转过－(90°－β)角度的回转矩阵.

式(2)通过σd→σod→σo1→σ1的转换，最终可将产形面上的啮合点在刀座动坐标系中的位置表达，转换到蜗杆动坐标系:

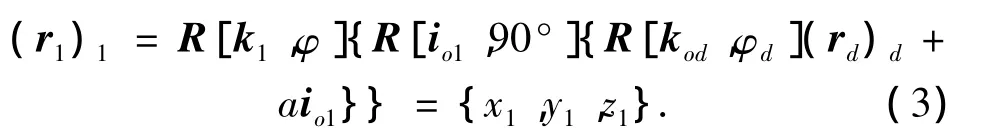
一次包络共轭条件方程为

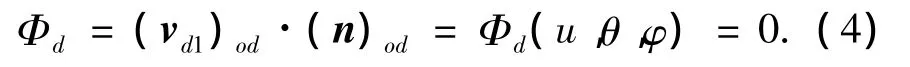
根据式(4)，可求出砂轮上的啮合点，将求得的啮合点参数代入式(3)，即可得到在σ1里蜗杆上的各个接触点.这些接触点就组成了在σ1里的蜗杆螺旋面Σ1.

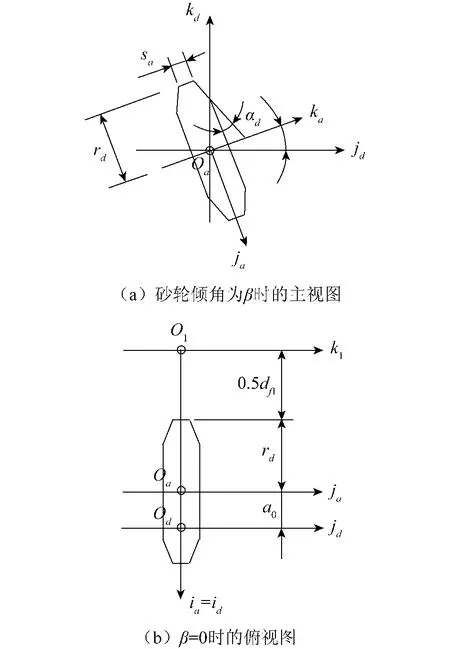
图2 双锥面砂轮在坐标系中的位置Fig.2 The position of dual-cone grinding wheel at the coordinate system

双锥面二次包络蜗轮的加工过程，是以滚刀齿面作为成型面，进行二次包络对蜗轮齿面的成形.因此，建立蜗轮齿面模型即为求解二次包络过程中产出的蜗轮齿面啮合点.

通过σ1→σo1→σo2→σ2的转换，可获得啮合点在蜗轮动坐标系中的位置表达:

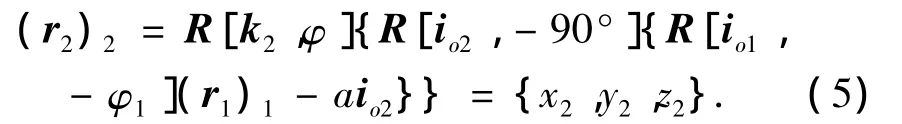
蜗杆副二次包络共轭条件方程为

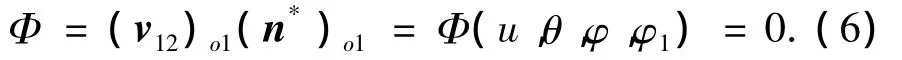
根据式(6)，可求出滚刀上的啮合点，将求得的啮合点的参数代入式(5)中，即可得在σ2里蜗轮上的各个接触点.而所有的接触点就构成了在σ2里蜗轮齿面Σ2.

2 优化模型的建立

2.1 优化参数的选择

设计开发一套新的蜗轮蜗杆减速器，首先应提出中心距a和传动比i这2个基本条件.蜗杆的头数z1和蜗轮的齿数z2根据传动比i的要求进行选择.此外，针对双锥面二次包络环面蜗杆传动，还需要确定其他3个重要的参数，分别是蜗杆分度圆直径系数k1、主基圆直径系数k2和产型面倾角β.如表1所示，这3个参数又影响到蜗杆副其他的几何参数，从而影响蜗轮蜗杆减速器的综合性能.常规设计时，k1、k2和β都是根据经验在推荐的一定的范围内选取的，为此，本文选择这3个参数作为所建立的优化模型的优化参数，即:

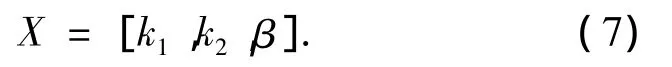
表1 双锥面二次包络环面蜗杆副部分几何参数Table 1 The geometric parameters of the dual-cone double enveloping hourglass worm gear pair

由第1节可知，蜗轮蜗杆副的齿面模型，与参数αd、sa、a0、β、a、rd有关.其中a根据设计要求确定，rd根据加工的条件决定，均可设为一定值;αd、sa与蜗杆副中的主基圆直径db、蜗杆分度圆压力角α等密切相关，受优化参数k2的影响;a0=a－0.5df1－rd，受优化参数k1的影响;而β即为优化参数之一.可见，蜗杆分度圆直径系数k1、主基圆直径系数k2和产型面倾角β这3个参数的选择，对蜗杆副的齿面模型有着直接的影响.

2.2 优化目标

在现有的平面环面蜗杆优化研究中，一般以提高润滑性能和减小传动副体积为优化目标，但只是以环面蜗杆的一次接触性能为基础进行分析，没有将环面蜗杆双线接触的传动特性进行综合分析，而且也没有考虑二次接触线的分布位置.

本文对双锥面二次包络环面蜗杆优化设计的研究，基于优先提高性能的考虑，追求更高的传动效率和更优的承载能力2个方面性能.传动效率主要取决于润滑条件，可以蜗杆副传动时的油膜厚度为参考因素，承载能力则受接触线分布情况影响较大，因此选择油膜厚度最厚、一次和二次接触线分布范围最广作为优化目标.

2.2.1 油膜厚度的几何系数

根据弹性流体动压润滑理论，蜗杆副接触齿面间油膜厚度，可按道森(Dowson)公式进行计算:

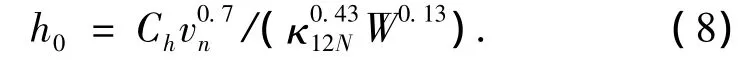
式中:κ12N表示蜗杆副沿瞬时接触线法向的诱导法曲率;W表示作用在单位齿宽上的载荷;Ch表示与润滑油的运动粘度、压粘系数及蜗杆蜗轮材料的弹性模量和泊松比有关的系数;vn表示相对卷吸速度.

蜗杆副沿αξ和αη方向的诱导法曲率为

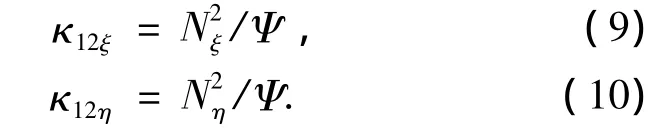
式中:Nξ和Nη为蜗杆副瞬时接触线上任一点处的法矢量N沿αξ和αη方向的分量，Ψ为蜗杆副二次包络曲率干涉界限函数.

根据式(9)、(10)，可求出蜗杆副沿瞬时接触线法向的诱导法曲率为

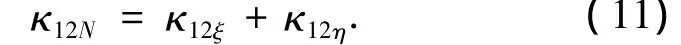
计算蜗杆副齿面间油膜厚度时，还需要求相对卷吸速度，即

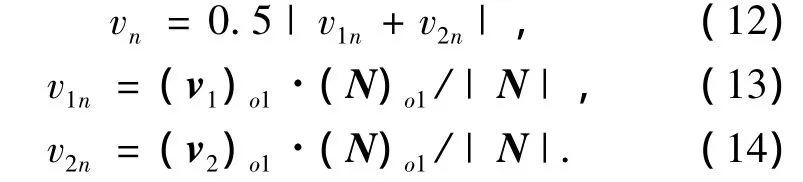
式中:v1和v2分别为蜗杆副啮合点处的蜗杆和蜗轮的线速度

在不考虑润滑油和蜗轮蜗杆材料性质，以及具体载荷的情况下，可选择油膜厚度的几何系数作为油膜厚度的评定参数［5］:

在蜗杆副不同的啮合角度和蜗杆齿面不同的啮合位置，油膜厚度的几何系数各不相同.为了获得最优的润滑条件，需要使接触面间的最小油膜厚度最大.由于蜗杆副啮入端蜗杆齿根处的油膜厚度最小，因此，以该位置处的油膜厚度几何系数建立优化目标模型，即

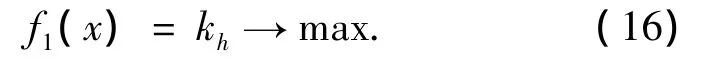
2.2.2 接触线分布

双锥面二次包络环面蜗杆具有双线接触的特性，包括一次接触线和二次接触线，其中一次接触线是产型面上接触线在蜗轮齿面上的再现，二次接触线是滚刀加工蜗轮的过程中产生的新接触线，传动过程中2类接触线同时作用.从工作起始角处开始，一次和二次接触线由蜗轮两侧面逐渐向蜗轮中心对称面附近移动.双锥面二次包络环面蜗杆副的一次和二次接触线在蜗轮齿面上的分布，不能过宽，也不能过窄.分布过宽时，工作起始角处的接触线在蜗轮齿面的外侧，这表示从工作起始角处开始的一定角度内，蜗轮外侧齿面未参与啮合，这将减少参与啮合的蜗轮齿数，从而降低了蜗杆副的承载能力.反之，当接触线在蜗轮齿面分布过窄时，接触线会集中于蜗轮齿面的中心对称面处，从而降低齿面强度，缩短了蜗杆副的使用寿命.

为了获得较好的分布区域，即接触线分布范围和蜗轮齿面的重合度更高，需要使工作起始角处的接触线，即最外侧的接触线，与蜗轮侧面的距离越小越好.为了具有代表性，选择该接触线位于蜗轮分度圆处的接触点为参考点建立目标模型，即

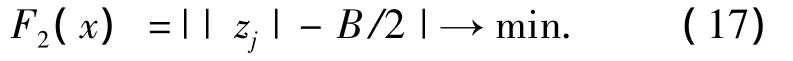
式中:zj表示接触线的位置方程，j=1表示一次接触线，j=2表示二次接触线，其计算见式(5);B表示蜗轮齿宽.

2.3 约束条件

如2.1节所述，与蜗杆分度圆直径系数k1、主基圆直径系数k2和产型面倾角β相关的约束主要考虑避免环面蜗杆根切和蜗杆齿顶变尖.

2.3.1 避免环面蜗杆根切

为了在加工环面蜗杆的过程中避免发生根切，需要保证一次包络的曲率干涉界线Ψd在蜗杆齿根环面之内.为建模方便，只需要保证根切曲线与蜗杆齿根环面之间的最小径向距离处不发生根切即可.经计算分析，可得一次包络曲率干涉界限在蜗轮齿面内的变化，如图3所示.

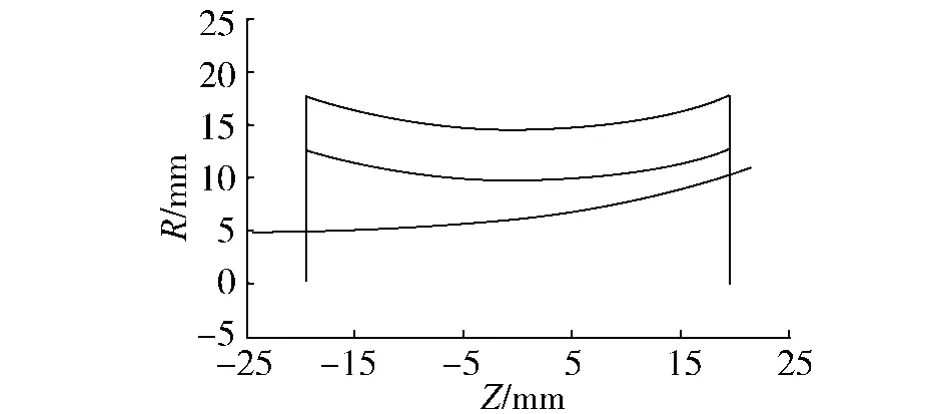
图3 一次包络曲率干涉界线Fig.3 Once-enveloping curvature interference limit line

曲率干涉界限径向距离变化趋势，如图4所示.可见，在工作起始角处，对应根切曲线的最右侧位置，其径向距离最小.所以选择约束条件:

式中:L表示根切曲线与蜗杆齿根环面之间的最小径向距离.

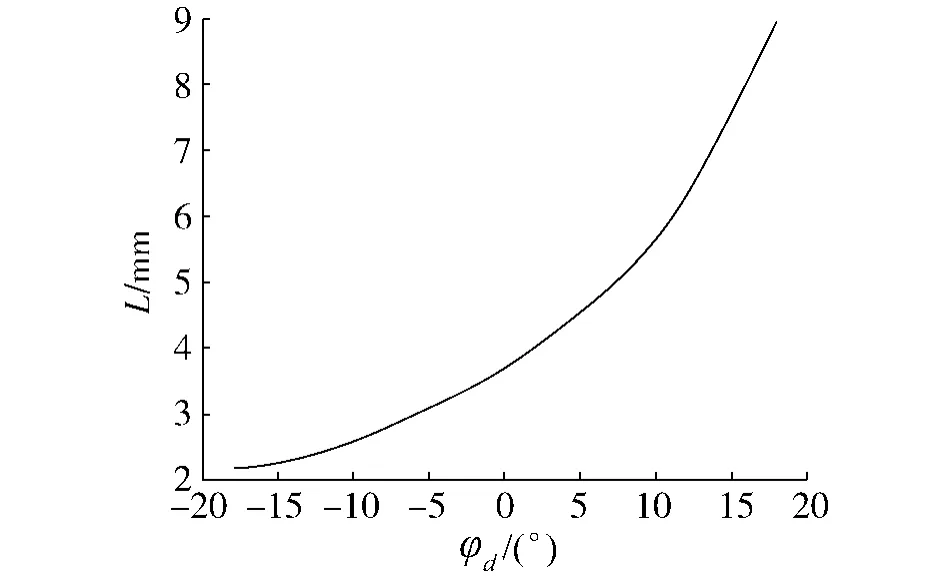
图4 L随φd的变化趋势Fig.4 The curve of L and φd

2.3.2 避免蜗杆齿顶变尖

环面蜗杆与普通圆柱蜗杆相比，成型面在蜗杆齿面上的啮合点随着刀座转角的变动而变动，所以蜗杆的齿顶宽度随着刀座转角变化.利用蜗杆左右两侧的齿面方程对蜗杆齿顶宽进行计算［10］，可知蜗杆边齿顶宽最小.为了避免蜗杆齿顶变尖，则需要保证:

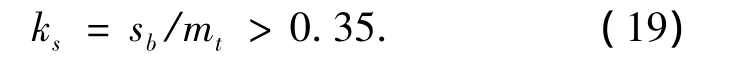
式中:ks表示边齿顶宽度系数;sb表示边齿顶宽;mt表示蜗轮端面模数.

2.4 模型的建立与求解

通过以上优化模型建立各要素的讨论，可确定双锥面二次包络环面蜗杆副多目标优化模型:

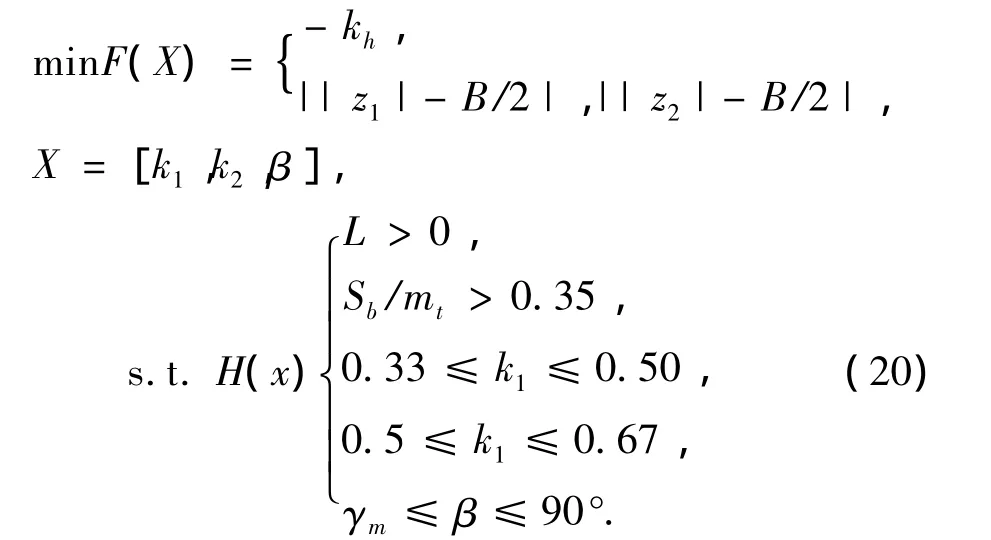
利用浙江大学机械设计研究所开发的柔性优化软件FlxOpt，建立上述优化模型.设定油膜厚度的几何系数和接触线分布的权重各为0.5，而在油膜厚度几何系数和接触线分布中，又分别设定一次接触线二次接触线的权重为0.5，如图5所示.

图5 柔性优化软件FlxOpt界面Fig.5 Interface of the flexible optimization designing software FlxOpt

3 双锥面二次包络环面蜗杆副优化设计实例

设计的双锥面二次包络环面蜗杆传动的中心距为a=75 mm，传动比i=40，采用单头蜗杆，蜗轮齿数为40.加工时，取砂轮半径rd=100 mm.取原始优化参数X=［0.35，0.63，10°］，经优化之后所得参数为X=［0.37，0.62，10.5°］.模型目标经优化后结果如表2所示.

表2 优化结果对照表Table 2 Comparison of optimization results

根据双锥面二次包络环面蜗杆副的数学模型，选取u=0的位置，即蜗轮齿根处，对其油膜厚度几何系数kh进行计算分析，结果如图6.对双锥面二次包络环面蜗杆副的接触线进行计算分析，结果如图7、8.

图7中，线1及1'为工作起始角处(φ2=－17.7°)的一次接触线和二次接触线，线2～9和线2'～8'对应的φ2从－14°以4°的增量递增，最后线10为工作结束角处(φ2=17.7°)的一次接触线.

图8中表示了蜗杆副的双线接触性能.经计算可知，优化前当φ2=－15.1°时，蜗轮齿面上开始出现二次接触线，蜗杆副开始具有双线接触的性能，而当φ2=13.2°时，齿面上的二次接触线消失;而优化后，当φ2=－16.8°时，蜗轮齿面上开始出现二次接触线，当φ2=14.6°时，齿面上的二次接触线消失.

由表2及图6～8可见，经过优化后，双锥面二次包络环面蜗杆副在约束的范围内，油膜厚度几何系数有所提高，其接触线分布范围与蜗轮齿面的重合度也有所提高，并且还具有了更长的双线接触区域.

为了从实验中对优化模型的效用进行分析，本文设计并搭建了用于实际数据测试的试验平台和数据处理系统.其中试验平台设计方案如图9所示.利用自主研制的双锥面二次包络环面蜗杆副加工设备，根据优化前后的设计参数，加工了2套用于对比实验的环面蜗杆减速器.对这2套环面蜗杆减速器，采用相同的装配和安装方式，并且使用同种润滑油.最后，利用搭建的蜗杆减速器试验平台对转速、转矩和传动效率进行了测试.

经过测试可以得到，双锥面二次包络环面蜗杆副减速器在优化前最高传动效率为57.39%，而优化后的最高传动效率能够达到62.56%.通过上述实验数据可知，利用上述多目标优化模型，对双锥面二次包络环面蜗杆副进行优化后，其传动性能有了一定的提高，从而证明该优化模型具有实际的效能.

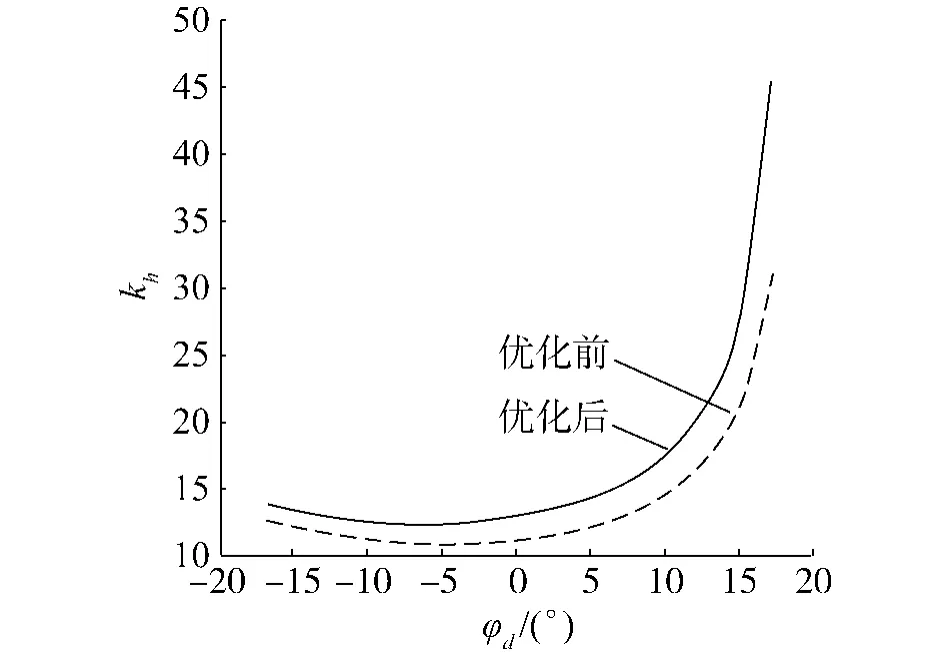
图6 优化前后的油膜厚度几何系数Fig.6 The geometrical coefficient of the oil film thickness before and after optimization

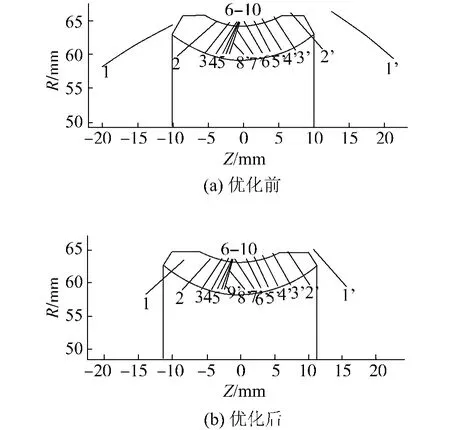
图7 优化前、后接触线在齿面上的分布情况Fig.7 The distribution of the contact lines before and after optimization

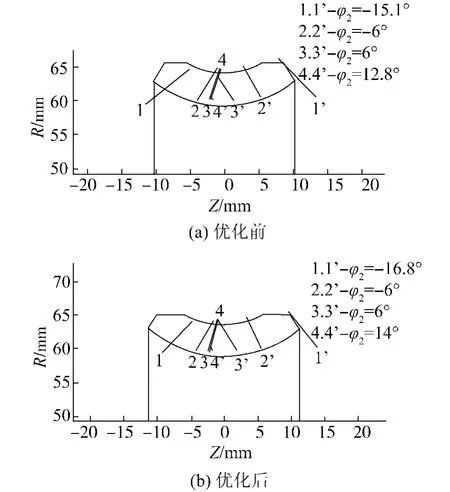
图8 优化前、后蜗杆副双线接触性能分析Fig.8 Analysis of dual-line contact performance before and after optimization

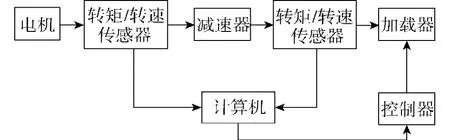
图9 试验平台设计方案Fig.9 Design of the test platform

4 结论

1)与普通圆柱蜗杆副相比，润滑性能和双线接触体现了双锥面二次包络环面蜗杆副优越的传动和承载性能，本文集中这2个方面的内容为优化目标，建立了多目标优化模型.

2)在考虑润滑性能这一优化目标时，选取油膜厚度的几何系数作为油膜厚度的评定参数.而在考虑承载能力这一优化目标时，不仅考虑了一次接触线的分布，而且同时考虑了二次接触线的分布情况.

3)通过理论分析和实验测试对优化前后的双锥面二次包络环面蜗杆副进行了对比，验证了该模型的有效性，为后续深入研究的开展提供了参考的方向.

［1］SIMON V.The influence of gear hobbing on worm gear characteristics［J］.Journal of Manufacturing Science and Engineering，2007，129(5):919-925.

［2］LITVIN F L，PEREZ I G，YUKISHIMA K，et al.Design， simulation of meshing，and contact stresses for an improved worm gear drive［J］.Mechanism and Machine Theory，2007，42(8):940-959.

［3］HILTCHER Y，GUINGAN M，VAUIANY J P.Numerical simulation and optimisation of worm gear cutting［J］.Mechanism and Machine Theory，2006，41(9):1090-1110.

［4］SU Daizhong，QIN Datong.Integration of numerical analysis，virtual simulation and finite element analysis for the optimum design of worm gearing［J］.Journal of Materials Processing Technology，2003，138(1-3):429-435

［5］黄安贻，夏江敬，张仲甫.平面二次包络环面蜗杆传动多目标优化设计［J］.机械设计，2003，20(9):40-45.

HUANG Anyi，XIA Jiangjing，ZHANG Zhongfu.Design of multi-target optimization for planar quadratic ring enveloped worm gear drive［J］.Journal of Machine Design，2003，20 (9):40-45.

［6］谭昕，徐林红，周红.基于润滑性能优先的平面二次包络环面蜗杆副参数优化设计［J］.机械设计与制造，2005，42(10):21-23.

TAN Xin，XU Linhong，ZHOU Hong.Parameter optimization design for planar double enveloping hourglass worm gear drive based on the lubricating property［J］.Machinery Design＆Manufacture，2005，42(10):21-23.

［7］张光辉，张太萍，罗文军.准平面二次包络环面蜗杆传动参数选择及优化［J］.机械传动，2007，31(2):4-8.

ZHANG Guanghui，ZHANG Taiping，LUO Wenjun.Selecting and optimizing of the parameters on quasi-plane double enveloping hourglass worm drive［J］.Journal of Mechanical Transmission，2007，31(2):4-8.

［8］王进戈，张均富，邓星桥，等.无侧隙双滚子包络环面蜗杆传动的参数优［J］.机械工程学报，2010，46(21):7-12.

WANG Jinge，ZHANG Junfu，DENG Xingqiao，et al.Parameter optimization of the non-backlash double-roller enveloping hourglass worm gearing［J］.Chinese Journal of Mechanical Engineering，2010，46(21):7-12.

［9］邓星桥，王进戈，张均富，等.基于遗传算法的无侧隙双滚子包络环面蜗杆传动的参数优化设计［J］.四川大学学报:工程科学版，2010，42(2):250-254.

DENG Xingqiao，WANG Jinge，ZHANG Junfu，et al.Optimization design of the non-backlash double-roller enveloping hourglass worm＇s parameters based on genetic algorithm［J］.Journal of Sichuan University:Engineering Science E-dition，2010，42(2):250-254.

［10］董学朱.环面蜗杆传动设计和修形［M］.北京:机械工业出版社，2004:70-84.

DONG Xuezhu.Design and modification of hourglass worm gearing［M］.Beijing:China Machine Press，2004:70-84.