欧拉型光线寻优算法

沈继红，李加莲，李焱

(1.哈尔滨工程大学理学院，黑龙江哈尔滨150001;2.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001)

优化问题存在于科学研究和工程应用中的各个领域.传统优化方法存在诸多的局限性，难以解决日益增多的复杂问题，而以生物智能或自然现象为基础的智能算法，通过模拟自然界的物理或生态过程以及其各自算法本身的寻优机制，对最优化问题进行求解并实现全局收敛，具有简单通用、鲁棒性好、适于并行处理等特点，因此成为解决复杂优化问题的一种新途径.这方面的研究很多，如遗传算法、模拟退火算法、蚁群算法、粒子群算法等.受启发于费马原理［1］，沈继红于2007年提出一种新型的智能优化算法——光线寻优算法［2］(light ray optimization algorithm，LRO).LRO算法通过模拟光线在不均匀介质中的传播过程进行优化搜索，它不依赖于函数梯度信息，需要调整的参数少，简单容易实现［3］.该算法将搜索区域设想为填充了不同折射率的介质区域，把介质区域划分成很多小区域(如矩形网格、正六边形网格［4］)，光在此小区域的传播速度为小区域中心点所对应的目标函数值，即此小区域被近似看成均匀介质.当搜索区域被分成足够多的小区域，即每一小区域足够小时，LRO的寻优路径实际是光线路径的近似［5-6］.LRO中位置的更新是通过求解光线和其所射到网格边的交点，所以每迭代一次，都要判断光线射到网格的哪一边，而且随着目标问题维数的增加，判断的次数增多，寻优速度减慢.本文针对LRO推广到高维收敛速度慢的问题，研究了光线方程欧拉数值解法与LRO迭代公式的关系，将与欧拉法相差的项加到LRO中得到一种改进LRO算法(improved light ray optimization，ILRO)，这不仅使精度提高一阶，而且大幅提高了收敛速度.

1 光线寻优算法

1.1 算法描述

以如下优化问题为例:

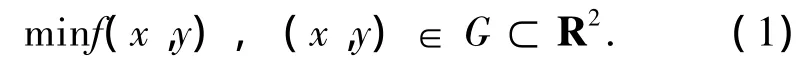
其中，对于∀(x，y)∈G，均满足f(x，y)＞0.用水平及竖直的直线划分搜索域G，这样得到很多小矩形网格Di.如图1，以第m次迭代为例，设从点(x(m)，y(m))以方向(p(m)，q(m))发出的一束光射到网格水平边上的点(x(m+1)，y(m+1))，则

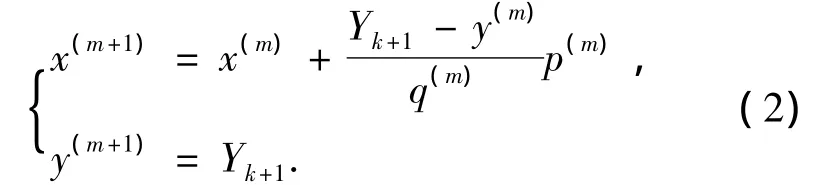
式(2)是通过计算光线与所射到边y=Yk+1的交点而得.(p(m)，q(m))与(p(m+1)，q(m+1))的迭代关系满足以下2点:

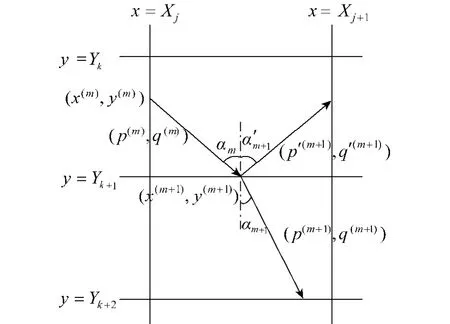
图1 模拟反射和折射的最优搜索路径Fig.1 The optimal searching path simulating reflection and refraction

1)如果满足全反射条件，即vm+1sin αm＞vm，发生反射(如图1)，方向的迭代关系满足反射定律: α'm+1=αm，其中αm为入射角，αm+1为反射角，则

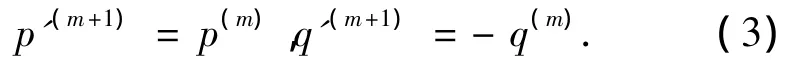
2)如果vm+1sin αm≤vm，发生折射(如图1)，方向的迭代关系满足折射定律其中αm为入射角，αm+1为折射角，则

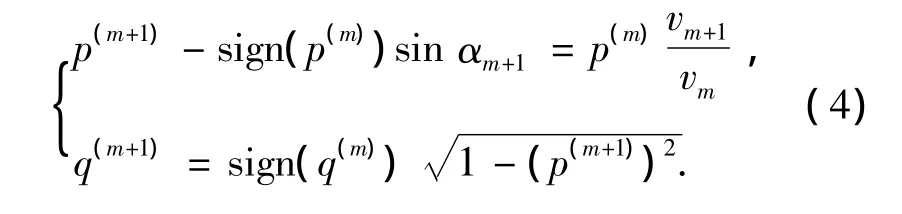
当光线射到网格的竖直边上时，类似的可推得位置和方向的迭代公式.

1.2 算法流程

根据上述分析，LRO算法具体实现步骤如下:

1)选定矩形网格的宽h和高τ，对搜索区域G进行划分.

2)随机选定初始点(x(0)，y(0))和初始方向(p(0)，q(0))，记录光线所在的网格.

3)判断光线射到所在网格的哪一边上，从而计算下一个迭代点.

4)如果满足停止条件，转步骤6)，否则，转步骤5).

5)判断是否满足全反射条件，如果满足，按照反射定律计算下一个搜索方向，否则，按照折射定律计算下一个搜索方向.记录光线所在的下一个网格，转步骤3).

6)停止优化搜索并输出最优值.

2 算法收敛性的基本理论

设光在折射率n=n(x，y)连续变化的区域传播，其所满足的微分方程［7］:

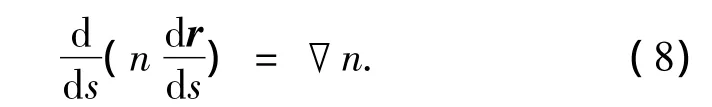
定理1 设二维搜索域G中光的传播速度为v(x，y)，如果v(x，y)二阶连续可导，那么任意选定G中的初始点，任意给定初始方向，可确定与它们相对应的唯一一条光线路径.

证明 因为:

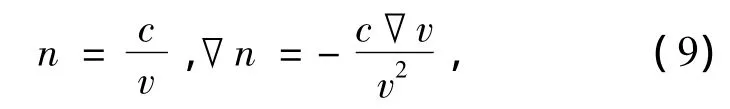
式中:c为光在真空中的速度.将式(9)代入光线微分方程(8)得

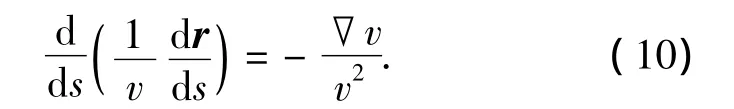
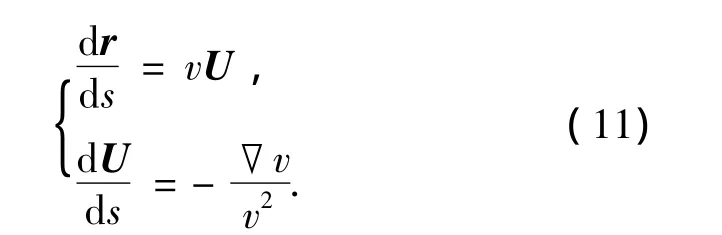
令r=(x，y)T，U=(u，w)T，方程组(11)可化为

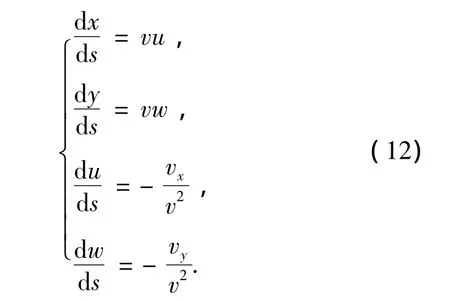
由定理已知条件v(x，y)二阶连续可导，可知方程组(12)的右端函数具有连续偏导数，因此满足微分方程组解的存在唯一性定理，即由初值可以确定方程组(12)的唯一解.

在定理1中，v(x，y)取为目标函数f(x，y)，即v(x，y)=f(x，y)，以下的讨论中也是如此.

定理2 在LRO算法中，如果第m次迭代光线在网格水平边上发生折射，得到的方向迭代公式与光线方程欧拉数值解法相差，如果光线在竖直边上发生折射，得到的方向迭代公式与光线方程欧拉数值解法相差，其中λm为LRO算法第m次迭代的步长.

证明 用欧拉法解微分方程组(11).

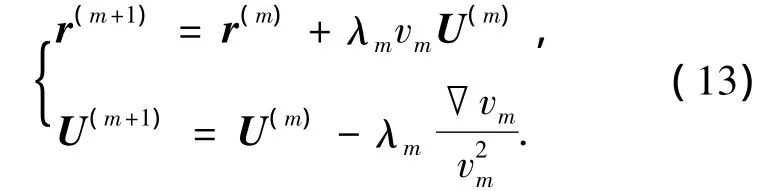
其中，

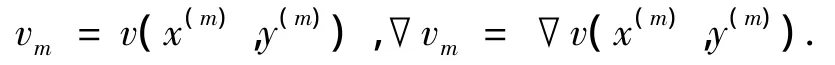
因为

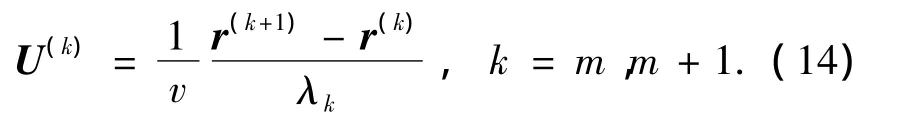
将式(14)代入式(13)得

考虑二维情形，则

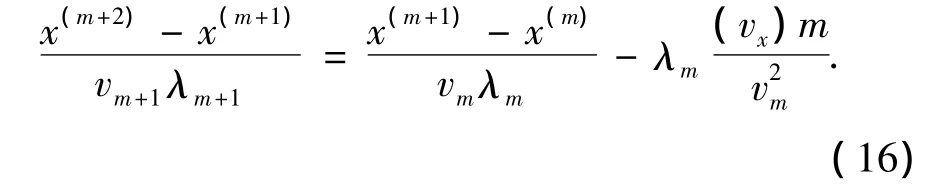
在LRO算法中，如图2，以在水平边上发生折射的情形为例，因为:

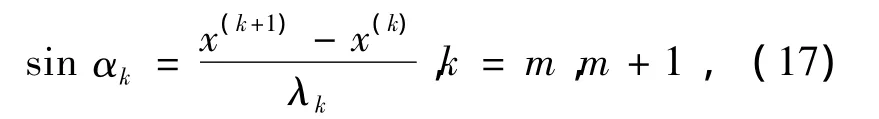
式中:λk为LRO算法第k次迭代的步长.由式(17)及折射定律得

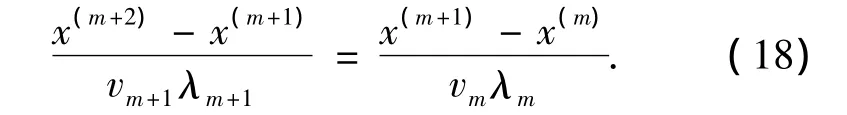
由LRO得到的式(18)和欧拉法解光线方程得到的式(16)相差同理可以得到，当光线在竖直边上发生折射时，相差为

定理3 LRO算法的寻优路径与光线路径的局部截断误差为O(λ).

证明 光线路径满足微分方程组(12)，则

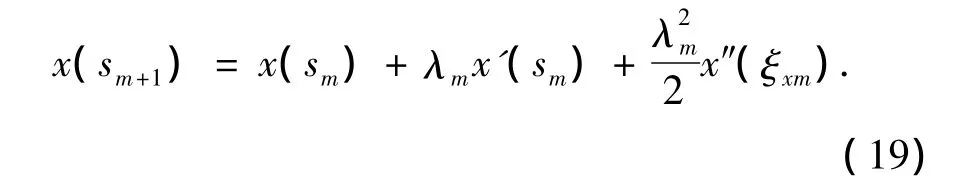
其中，ξxm∈(sm，sm+1).因为考虑局部截断误差，所以假设:

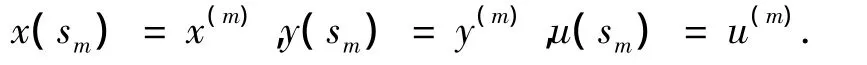
则

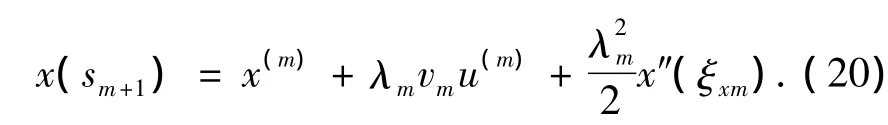
同理:

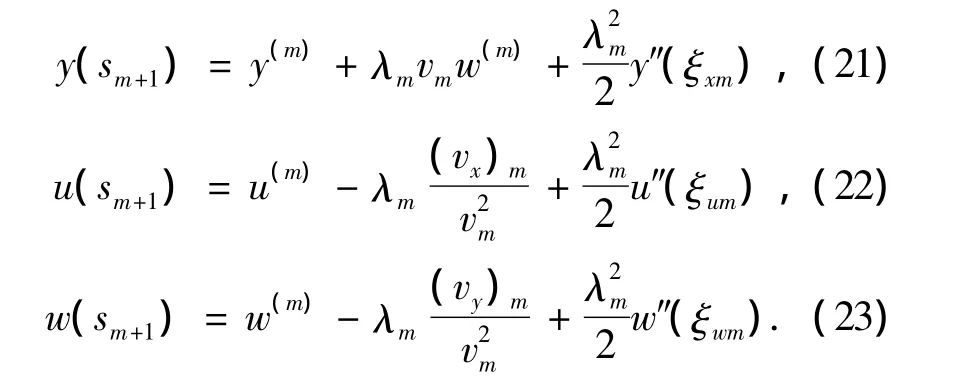
其中，ξym，ξum，ξwm∈(sm，sm+1)，则局部截断误差为

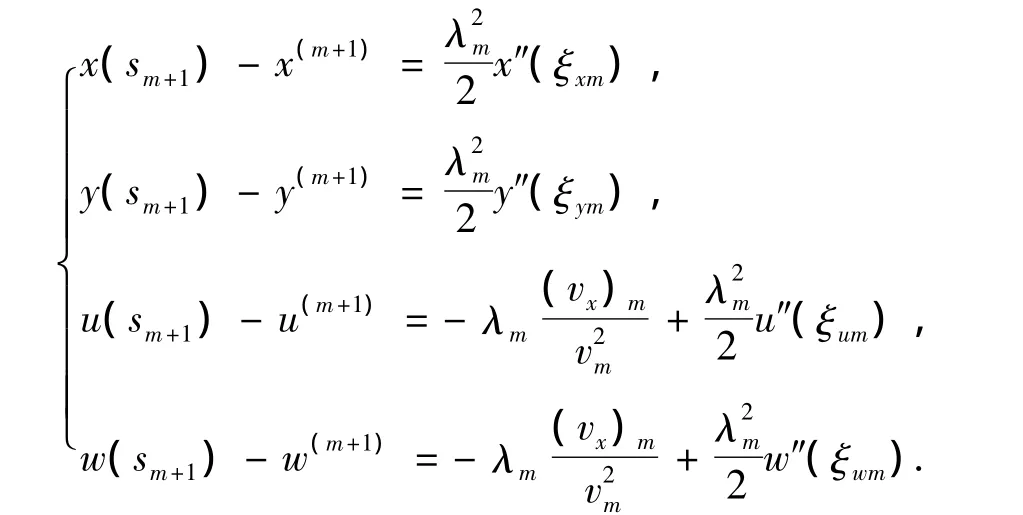
为了更清楚和直观的表述观点，定理1～3以二维为例进行阐述，实际上这些理论都可平行的推广到n维介质的情形.

3 改进光线寻优算法

LRO算法中位置的更新是通过求解光线与其所射到网格边的交点，二维情形下，网格有4条边，所以每迭代一次都要做4次判断，从而确定光线射到哪一条边上.三维情形下，网格有6个面，需要判断6次.以此类推，n维情形需要判断2n次.随着维数的增加，判断的次数增多，所以计算时间增多，收敛速度变慢，这是LRO推广到高维遇到的主要困难.根据定理2，将与欧拉法相差的项加到LRO中，从而得到一种改进的LRO算法(ILRO)，不仅将精度提高了一阶，而且使得寻优速度大大加快，解决了LRO推广到高维运行速度慢的问题.具体推导过程如下.

首先将与欧拉法相差的项加到LRO中，并固定步长，可得如下迭代公式:

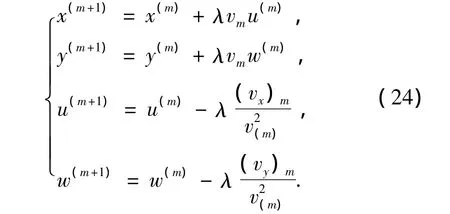
因为

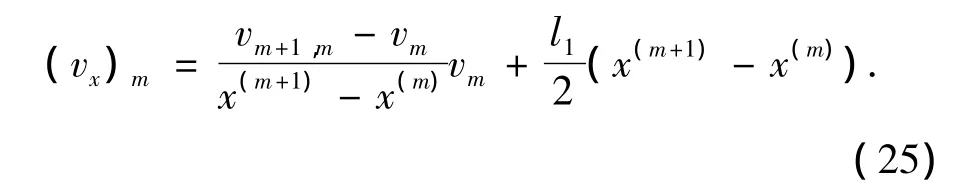
其中:

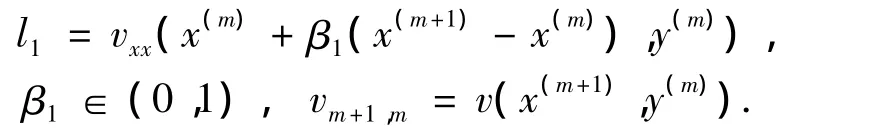
同理可得

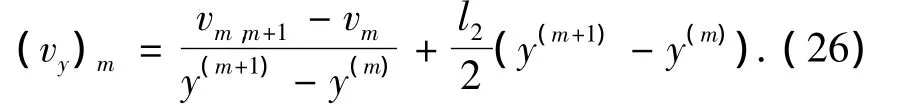
将式(25)、(26)代入式(24)得

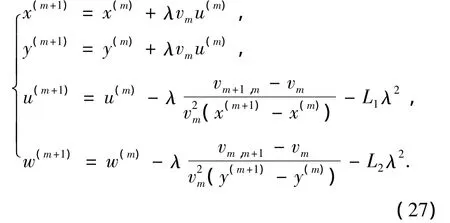
其中，

略掉式(27)中的O(λ2)项，即为ILRO的迭代公式，则由式(20)～(23)，可得ILRO算法的局部截断误差:

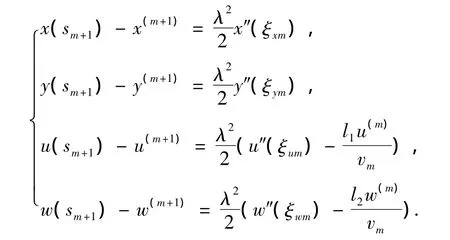
所以ILRO的局部截断误差为O(λ2)，其迭代公式可推广到n维:

以下给出ILRO算法的流程:

1)给定步长λ，随机选定初始点和初始方向，令m=0.

3)判断是否满足停止条件，如果满足，转步骤5)，否则转步骤4).

4)令m=m+1，转步骤2).

5)停止优化搜索并输出最优点.

4 改进算法与其他算法的对比仿真实验

为了检验ILRO算法的的性能，对文献［8］中的6个标准测试函数进行仿真实验，测试函数如表1所示.

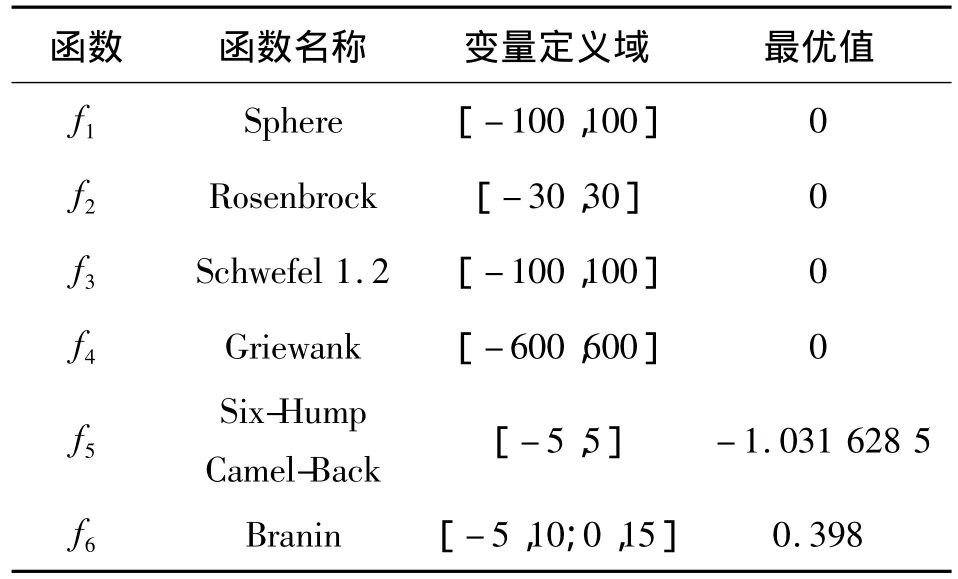
表1 测试函数Table 1 Test functions

表1中f1～f3为单峰函数，f4～f6为多峰函数，f5、f6为2维函数.采用文献［9］中的函数变换法，选择适当的M值加到各函数中，使得它们最优值均变为1.所有实验均在处理器为E5400@2.70 GHz 2 G内存的PC机上运行.

4.1 ILRO中步长对寻优精度的影响

优化函数为f1、f2，步长分别为1、0.1、0.01，最大迭代次数分别为100、1 000、10 000，对不同的函数及步长，ILRO分别独立运行100次，因为维数越高时，网格越小精度越高的优势更加明显，所以给出40维函数的数值实验结果，见表2.可知，随着步长的减小，精度提高，但步长越小，迭代次数越多，相应的运行时间将越长.所以在精度要求范围内，选取适当大小的网格是很重要的.

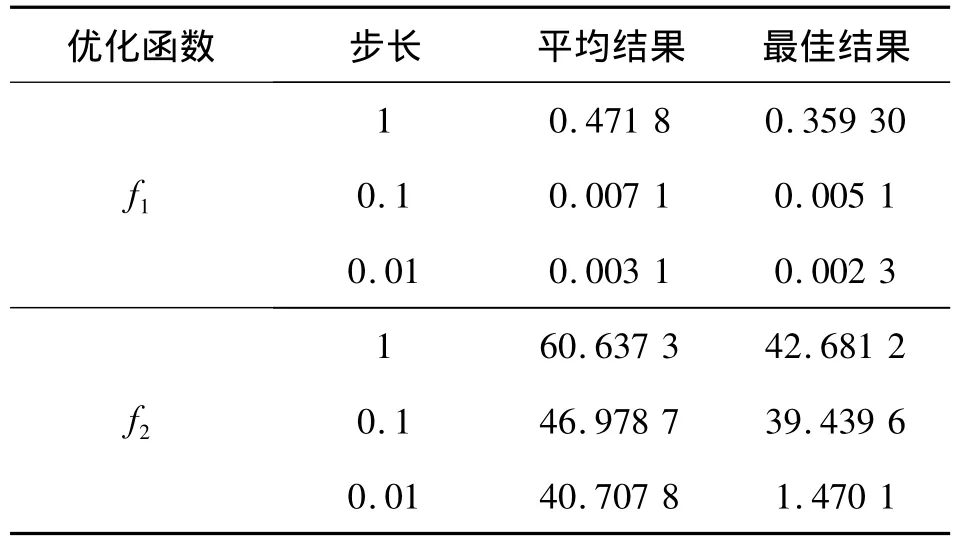
表2 步长对精度的影响Table 2 The influence of step length on accuracy

4.2 ILRO与LRO的比较法

优化函数为f1、f2，以二维为例(与LRO相比，ILRO计算速度的优势在低维时很明显)，ILRO步长0.1，LRO网格宽和高均为0.1.2种算法最大迭代次数均为1 000，分别独立运行100次，结果见表3.可见ILRO的平均迭代时间远远小于LRO.

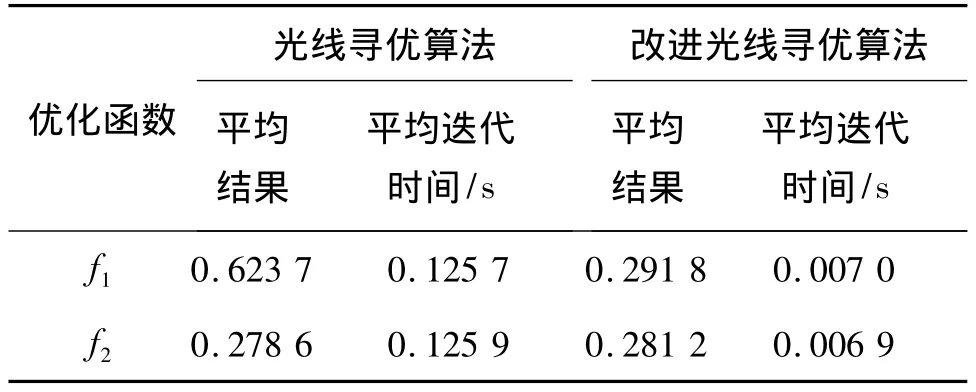
表3 ILRO与LRO的仿真结果比较Table 3 Comparison of simulation results of ILRO and LRO

4.3 ILRO与EGA和SPSO的比较

优化函数为f1～f6，30维(其他优化算法文献中经常选用的维数).为了比较的合理性，通过粗略地调节相关参数来获得合适的性能.测试中算法的参数设置如下:ILRO算法步长h为0.1;EGA交叉概率0.6，变异概率0.001，30维函数的编码长度20，群体规模80，2维函数的编码长度10，群体规模20; SPSO学习因子c1、c2均为1.4，惯性权重w=0.9，30维函数的粒子数100，2维函数的粒子数20.比较方法:设定最大迭代次数10 000，各测试函数的目标值(见表4第2列)，如果算法在达到最大迭代次数后仍未达到目标值，则认为算法没有成功收敛.针对不同的优化函数，3种算法分别独立运行50次，成功收敛实验的平均迭代时间及相应成功收敛率见表4.

由表4可知，对于30维函数f1～f4，无论从平均迭代时间还是成功收敛率角度考虑，ILRO均优于EGA和SPSO，这说明ILRO的收敛速度较快，收敛可靠性较高.对于2维函数f5～f6，从2个方面考虑ILRO都优于EGA，收敛成功率和SPSO持平，平均迭代时间要多于SPSO，这说明低维时，ILRO的收敛速度并没有SPSO快，其收敛速度的优势在高维时体现的较明显.EGA和SPSO通过参数的不断调整，也许能以更快的运行时间达到更高的精度，但这需要有一定的经验，并且不同的研究者可能得出完全不同的结果.ILRO只有步长一个参数需要调节，并且从理论上讲，步长越小，精度越高.所以作为一种新的智能算法，ILRO具有一定的优越性以及寻优潜能.

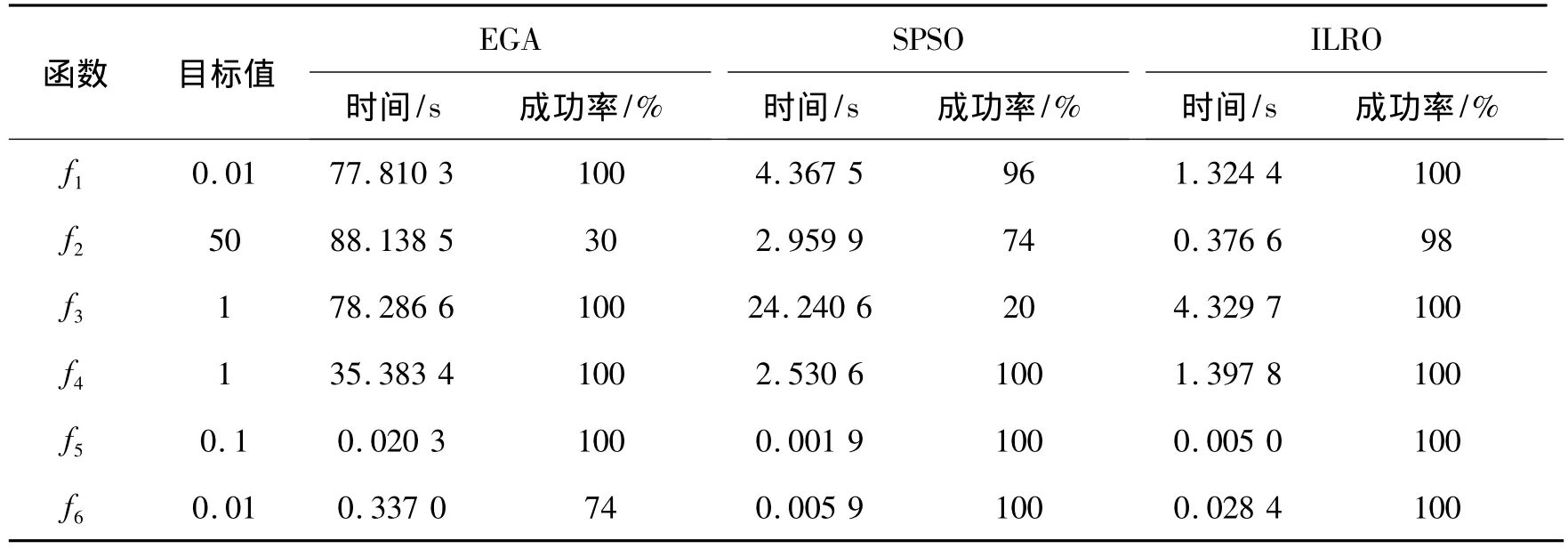
表4 ILRO与SPSO和EGA的仿真结果比较Table 4 Comparison of simulation results of ILRO，SPSO and EGA

5 结论

光线寻优算法是一种模拟光在变折射率介质中的传播路径进行最优值搜索的智能算法.作为一种新的算法，它为智能计算用于解决最优问题提供了新思路，并且具有可调参数少，结构简单容易实现等优点.研究了光线方程欧拉数值解法和光线寻优算法迭代公式的关系，通过将与欧拉法相差的项加到光线寻优算法中进行算法的改进，从而达到提高精度，加速收敛的目的.选用6个标准测试函数对改进光线寻优算法进行测试，实验结果表明:

1)改进光线寻优算法中步长越小，精度越高，搜索时间越长.

2)与光线寻优算法相比，改进光线寻优算法收敛速度的优势在低维时就很明显.

3)改进光线寻优算法的收敛速度和收敛成功率均优于保留精英遗传算法.

4)与标准粒子群算法相比，改进光线寻优算法的收敛成功率较高，求解二维函数的收敛速度较慢，30维函数的收敛速度较快.

深入分析算法的寻优机理和收敛性，改进算法(如考虑变步长)，提高算法的收敛性能，拓宽算法的应用范围，将是今后研究的重点.

［1］姚启钧.光学教程［M］.北京:高等教育出版社，2008: 154-157.

YAO Qijun.Optics course［M］.Beijing:Higher Education Press，2008:154-157.

［2］SHEN Jihong，LI Yan.An optimization algorithm based on optical principles［J］.Advances in Systems Science and Applications，2009，9(4):647-655.

［3］SHEN Jihong，LI Yan.Light ray optimization and its parameter analysis［C］//Proceeding of the 2009 International Joint Conference on Computational Sciences and Optimization.Sanya，China，2009:918-922.

［4］沈继红，李焱.基于正六边形网格的光线寻优算法［C］//中国运筹学第十届学术交流会.北京，中国，2010:21-22.

SHEN Jihong，LI Yan.Light ray optimization algorithm based on hexagon grid［C］//The 10th Academic Conference of Chinese Operational Research Society.Beijing，China，2010:21-22.

［5］SHEN Jihong，LI Jialian.The principle analysis of light ray optimization algorithm［C］//2010 Second International Conference on Computational Intelligence and Natural Computing.Wuhan，China，2010:154-157.

［6］SHEN Jihong，LI Jialian.Light ray optimization algorithm and convergence analysis for one dimensional problems［C］//2011 International Conference on Fuzzy Systems and Neural Computing.Hong Kong，China，2011:103-106.

［7］刘得森.变折射率介质理论及其技术实践［M］.重庆:西南师范大学出版社，2005:14-26.

LIU Desen.Theories and technologies of gradient refractive index medium［M］.Chongqing:Southwest Normal University Press，2005:14-26.

［8］YAO X，LIU Y，LIN G.Evolutionary programming made faster［J］.IEEE Transactions on Evolutionary Computation，1999，3(2):82-102.

［9］SHEN Jihong，LI Yan.Light ray optimization with function transform［C］//The 8th International Conference on Optimization:Techniques and Applications.Shanghai，China，2010:21-22.

［10］MAJUMDAR J，BHUNIA A K.Elitist genetic algorithm for assignment problem with imprecise goal［J］.European Journal of Operational Research，2007，177:684-692.

［11］EBERHART R C，KENNENEDY J.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks.Perth，Australia，1995:1942-1948.

［12］秦洪德，石丽丽.一种新型的被动启发式粒子群优化算法［J］.哈尔滨工程大学学报，2010，31(10):1298-1302.

QIN Hongde，SHI Lili.A new passive heuristic particle swarm optimization algorithm［J］.Journal of Harbin Engineering University，2010，31(10):1298-1302.