一类单圈图的Laplacian谱刻画

卢鹏丽，王旭柱，陈作汉

(兰州理工大学计算机与通信学院，甘肃兰州730050)

本文所涉及的图都是简单无向图.设图G= (V(G)，E(G))的顶点集和边集分别为V(G)={v1，v2，…，vn}和E(G)，其中v1，v2，…，vn按顶点的度非递增排列.设A(G)=(auv)是图G的邻接矩阵，当u和v相邻时，auv=1，当u和v不相邻时，auv=0.di= di(G)=dG(vi)是顶点vi的度，D(G)是对角元素为{d1，d2，…，dn}的n×n对角矩阵，则矩阵L(G)= D(G)－A(G)称为图G的Laplacian矩阵.显然，L(G)是一个最小特征值为0的半正定对称矩阵.设μ1≥μ2≥…≥μn(=0)是L(G)的特征值，它们构成了图G的Laplacian谱.如果2个图有相同的Laplacian谱，就说他们是Laplacian同谱图.如果与图G同Laplacian谱的图都与图G同构，则称图G可由它的Laplacian谱确定.

关于“哪些图可由它们的谱确定?”这个问题的背景，建议读者参阅文献［1－2］，到目前为止，只有少量结构特殊的图被证明了能由它们的谱确定［1－4］.因此，寻找新的谱确定图是一个有趣的问题.

文献［3］证明了lollipop图(表示为Cn，g，它是在一条顶点数为n－g的路图的一个悬挂点上连接一个圈Cg得到的图)能由其Laplacian谱确定.文献［5］证明了图H(n;q，n1，n2)(它是在一个圈Cq的同一个顶点上悬挂2条路Pn1，Pn2而构成的图，n是它的顶点数)能由其Laplacian谱确定.

本文证明了图H(n;q，n1，n2，n3)可由其Laplacian谱确定.

1 基本引理

引理1［1］对于图G，由其邻接谱和Laplacian谱可得图G的下列性质:

1)顶点数，

2)边数，

3)G是否是正则图.

由其邻接谱可得:

4)任意长度的闭回路数，

5)图G是否是二部图.

由其Laplacian谱可得:

6)分支数目，

7)生成树数目，

8)顶点的度平方和.

引理2［1］设N是一个n×n的对称矩阵，其特征根为α1≥α2≥…≥αn.N的m阶主子矩阵的特征根为α1'≥α2'≥…≥αm'，则αi≥αi'≥αn－m+i，i= 1，2，…，m.

引理3［6］设A=［aij］是一个n阶方阵，令

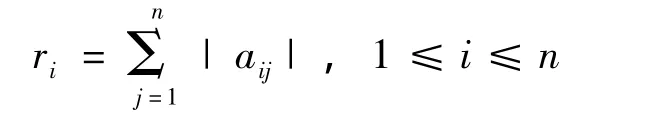
是矩阵A第i行元素的绝对值的和，则

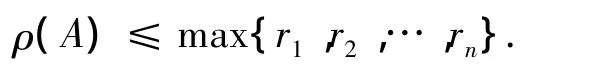
式中:ρ(A)是矩阵A的最大特征值.相似地，对于矩阵A中列元素的绝对值的和，该不等式也成立.

引理4［7－8］设图 G的顶点集和边集分别为V(G)≠Ø和E(G)≠Ø.则

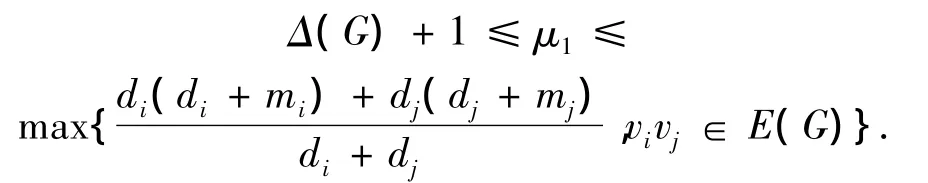
式中，Δ(G)表示图G中顶点最大的度，mi表示图G中与顶点vi邻接的顶点的度数的平均值.

本文将方阵B的特征多项式表示为

式中，I是单位阵.特殊地，当B=L(G)时，将φ(L(G))写成φ(G;x)或直接写成φ(G)，称φ(G)为图G的Laplacian特征多项式.

引理5［5］设图G有n个顶点m条边，deg(G)=(d1，d2，…，dn)为它的非递增度序列.则φ(G)的前4个系数为

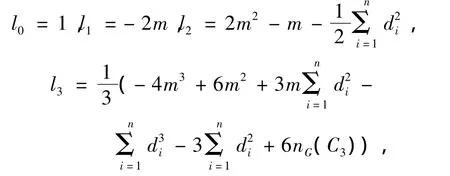
式中:nG(C3)表示图G中三角图的数目.

引理6［4］设图G是一个顶点数n≥3的连通图，则μ2≥d2.

这里，用符号Φ表示一个森林，它的每个分支都是一棵树.用p(Φ)表示森林Φ中各个分支的顶点数的乘积.

引理7［9］多项式φ(G)的系数li可由下式得出:

对图G的具有i条边的所有子森林求和.

设Pn和Cn分别是具有n个顶点的路和圈，Bn是从L(Pn+1)中删除路Pn+1的2个端点之一对应的行和列后得到的n阶矩阵，Hn是从L(Pn+2)中删除Pn+2的2个端点对应的行和列后得到的n阶矩阵.

引理8［10］设φ(P0)=0，φ(B0)=1，φ(H0)= 1.则有:

通过简单的计算便能得到，φ(P1;4)=4.根据引理8中的递推公式，可以得到如下结论.

引理9

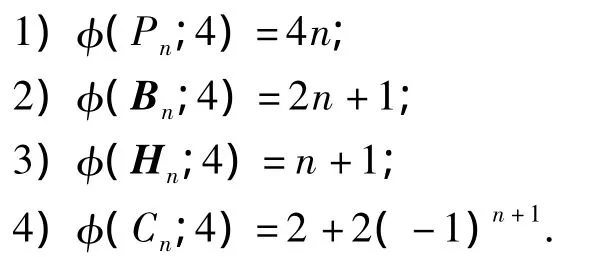
设v是图G的一个顶点，令Lv(G)是从L(G)中删去顶点v对应的行和列后得到的L(G)的主子矩阵.

引理10［11］设图G=G1u∶vG2是通过一条边连接图G1的顶点u和图G2的顶点v得到的图，则

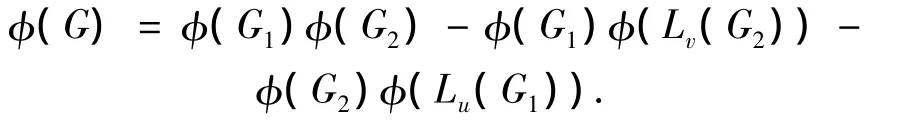
引理11［5］设图G是含有圈Cq的顶点数为n的连通单圈图.如果图G'与图G同Laplacian谱，则G'是一个含有圈Cq的顶点数为n的连通单圈图，而且:

2 主要结果

定理1 如果2个形如H(n;q，n1，n2，n3)的图同Laplacian谱，则它们必定同构.

证明 令图G=H(n;q，n1，n2，n3)(见图1).设G'=H(n;q'，n1'，n2'，n3')与图G同Laplacian谱.根据引理11，q'=q.则:

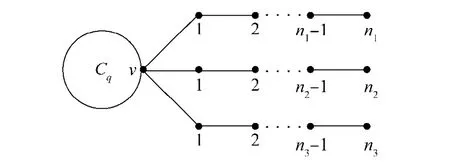
图1 图H(n;q，n1，n2，n3)Fig.1 The graph H(n;q，n1，n2，n3)

根据引理7，得到

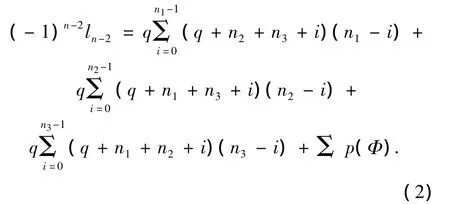
式中:Φ表示所有的在图G的圈Cq上删去2条边而得到的子森林.

相似地，

将式(3)～(5)代入式(2)，得到

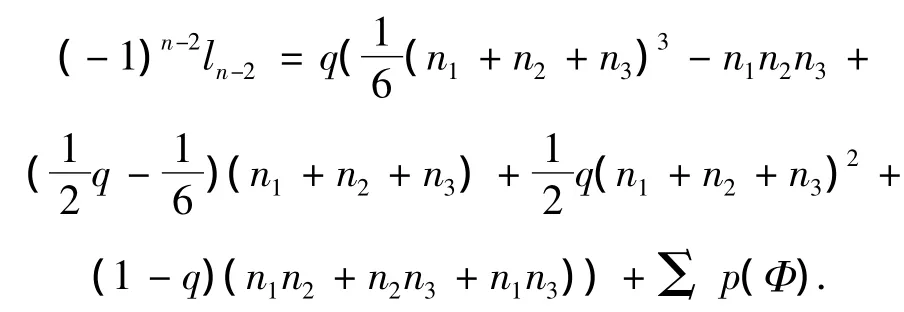
相似地，对l'n－2，有

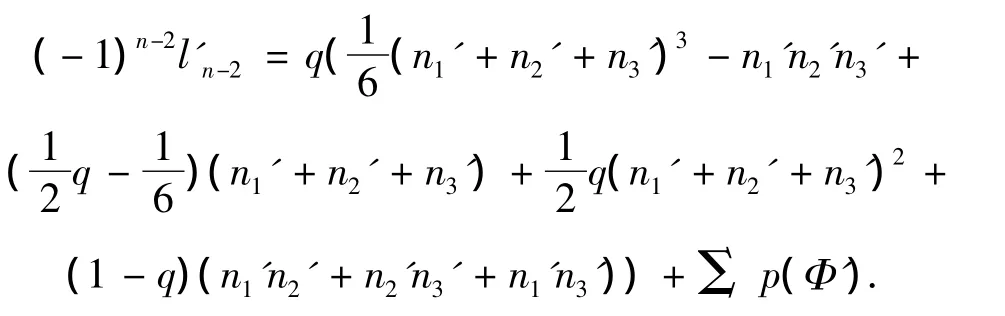
因为n1+n2+n3=n1'+n2'+n3'，所以，

因为ln－2=l'n－2，所以，

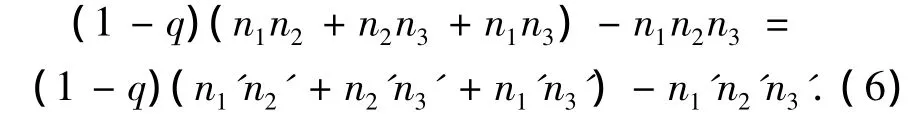
应用引理10，可以将图G的Laplacian特征多项式写成如下形式:

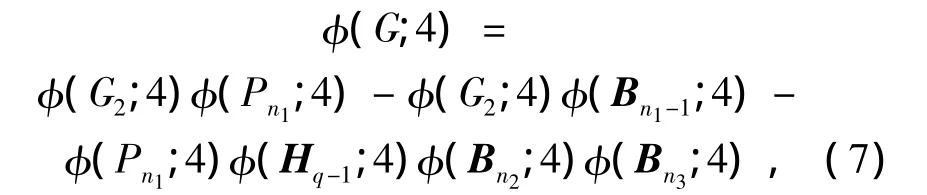
其中:

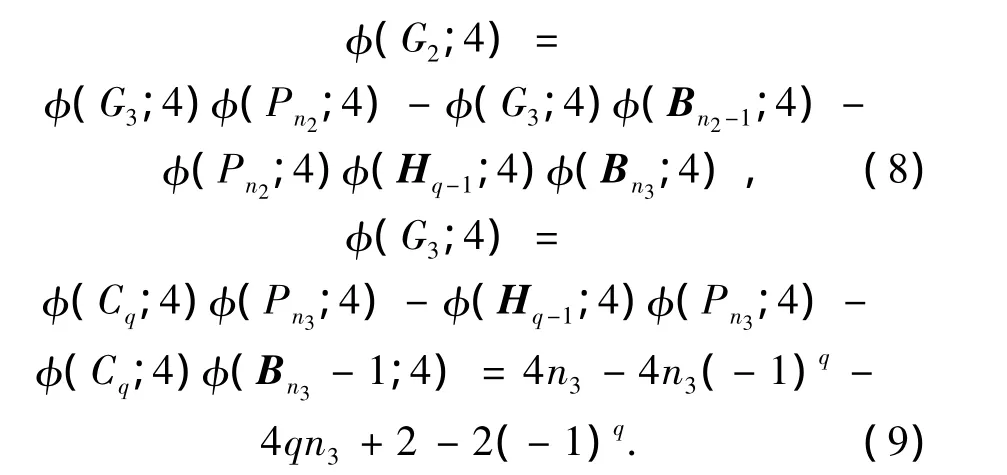
图G2=H(n－n1;q，n2，n3)，图G3=Cn－n1－n2，q.

将式(8)、(9)代入式(7)，根据引理8、9，可得

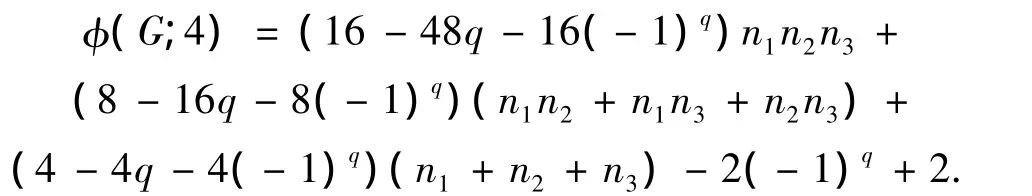
相似地，对于图G'同样有，

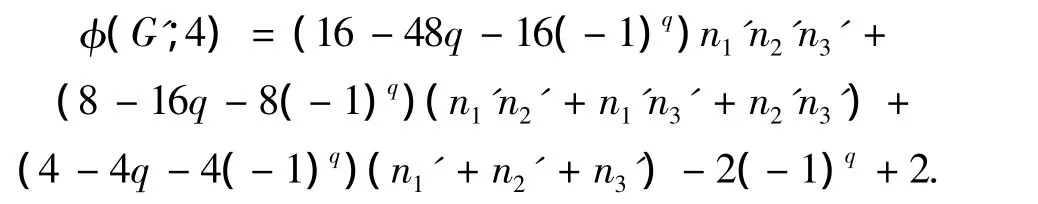
因为φ(G;4)=φ(G';4)，所以，

联立式(6)、(10)，解得

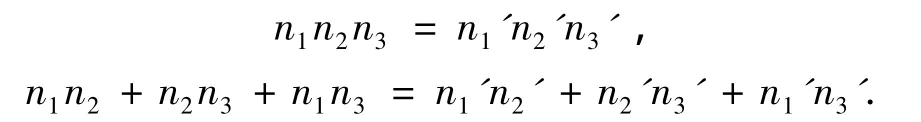
显然，n1、n2、n3与n1'、n2'、n3'分别是三次方程:

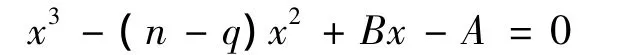
的根.所以图G与图G'同构.

定理2 图H(n;q，n1，n2，n3)由它的Laplacian谱确定.

证明 令G=H(n;q，n1，n2，n3).设图G'与图G同Laplacian谱.根据引理11，图G'是一个含有圈Cq的连通单圈图，它有n个顶点n条边.设图G'由xj'个度为j的顶点，j=1，2，…，Δ，其中，Δ是图G'中最大的度.根据引理4所以，Δ=d1(G')≤5.又max{ri(Lv(G))}=4，其中，i=1，2，…，n－1.根据引理3，μ1(Lv(G))≤4.

由引理2可得μ1(L(G))≥μ1(Lv(G))≥μ2(L(G))，即μ2(G)≤4.根据引理6，d2(G')≤μ2(L(G'))≤4，即d2(G')≤4.

因此，图G'至多有一个度大于4的顶点.所以，由引理1的1)、2)、8)和引理11得到

通过Maple解方程(11)，得到

现在，考虑下列情况:

1)当Δ=1时，x1'=1，x2'=n，x3'=－6，x4'=4;

2)当Δ=2时，x1'=2，x2'=－1+n，x3'=－6，x4'=4;

3)当Δ=3时，x1'=2，x2'=n，x3'=－7，x4'=4;

4)当Δ=4时，x1'=2，x2'=n，x3'=－6，x4'=3;

5)当Δ=5时，x1'=3，x2'=n－4，x3'=0，x4'=0.

因为xi'是非负整数，所以Δ=5.

所以，图G'的形式是H(n;q，n1'，n2'，n3').根据定理1，图H(n;q，n1'，n2'，n3')与H(n;q，n1，n2，n3)同构.

3 结束语

本文证明了图H(n;q，n1，n2，n3)可由它的Laplacian谱确定.因为一个图的Laplacian特征值决定它的补图的 Laplacian特征值［7］，因此，图H(n;q，n1，n2，n3)的补图也由它的Laplacian谱确定.

［1］CVETKOVIC M，DOOB M，SACHS H.Spectra of graphs: theory and applications［M］.3rd ed.Heidelberg-Leipzig: Johan Ambrosius Bart Verlag，1995:23-47.

［2］VAN DAM E R，HAEMERS W H.Which graphs are determined by their spectrum?［J］.Linear Algebra Appl，2003，373:241-272.

［3］HAEMERS W H，LIU X G，ZHANG Y P.Spectral characterizations of lollipop graphs［J］.Linear Algebra Appl，2008，428:2415-2423.

［4］LI J S，PAN Y L.A note on the second largest eigenvalue of the Laplacian matrix of a graph［J］.Linear and Multilinear Algebra，2000，48(20):117-121.

［5］LIU X G，WANG S J，ZHANG Y P，et al.On the spectral characterization of some unicyclic graphs［J］.Discrete Mathematics，2011，311(21):2317-2336.

［6］BRUALDI R A，CVETKOVIC D.A combinatorial approach to matrix theory and its applications［M］.Boca Raton: Chapman＆Hall/CRC Press，2009:180.

［7］KELMANS A K，CHELNOKOV V M.A certain polynomial of a graph and graphs with an extremal number of trees［J］.Journal of Combinatorial Theory，Series B，1974，16:197-214.

［8］LI J S，ZHANG X D.On the Laplacian eigenvalues of a graph［J］.Linear Algebra Appl，1998，285:305-307.

［9］BIGGS N L.Algebraic graph theory［M］.2nd ed.Cambridge:Cambridge University Press，1993:47-48.

［10］GUO J M.A conjecture on the algebraic connectivity of connected graphs with fixed girth［J］.Discrete Math，2008，308:5702-5711.

［11］GUO J M.On the second largest Laplacian eigenvalue of trees［J］.Linear Algebra Appl，2005，404:251-261.