Nanoparticle Migration in a Fully Developed Turbulent Pipe Flow Considering the Particle Coagulation*

LIN Jianzhong (林建忠)**, LIU Song (刘淞) and CHAN Tatleung (陈达良) China Jiliang University, Hangzhou 0018, China

2 State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China

3 Department of Mechanical Engineering, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong, China

1 INTRODUCTION

Fluid flows containing nanoparticles occur in a wide range of natural and engineering problems [1-5].Mechanism of the motion of these nanoparticles is of interest and has been investigated during the past several decades. Nanoparticles suspended in pipes have lots of application, such as enhanced heat transfer with nanoparticles in micro heat exchangers, toxic particle transport in the human lung, contamination control of microelectronic manufacture, and control of surface fouling of microfluidic devices.

There exists some literature addressing the motion of nanoparticles in the pipe flow. Ding and Wen [6]studied the particle migration in pressure-driven laminar pipe flows of relatively dilute suspension of nanoparticles. It is shown that particle concentration in the wall region can be much lower than that in the central core region. Jang et al. [7] performed experimental and theoretical investigation on the effective viscosity of mixture of Al2O3-water flowing through micrometer- and millimeter-sized circular tubes in the fully developed laminar flow regime. It is found that the effective viscosity of Al2O3-water increases nonlinearly with the volume concentration of nanoparticles even in the very low range and strongly depends on the ratio of the nanoparticle diameter to the tube diameter. Akbarinia and Behzadmehr [8] studied numerically fully developed laminar mixed convection of a suspension of water and Al2O3in a horizontal curved tube. The results showed that the nanoparticle volume fraction does not have a direct effect on the secondary flow, axial velocity and the skin friction coefficient. However, its effect on the entire fluid temperature could affect the hydrodynamic parameters when the order of magnitude of the buoyancy force becomes significant compared to the centrifugal force.Mirmasoumi and Behzadmehr [9] studied numerically laminar mixed convection of mixture of water and Al2O3in a horizontal tube. It is found that at the fully developed region the nanoparticle concentration does not have significant effects on the hydrodynamics parameters. However, its effects on the thermal parameters are important. Jwo et al. [10] experimentally studied the flow containing nanoparticles in the pipe with different mass fraction, flowing condition and the temperature associated with the pressure drop. The results demonstrate that the mixture of Al2O3/water increases the pressure drop, whereas an increase in temperature reduces the pressure drop. A new empirical equation for the friction factor in laminar flow was developed. Lin et al. [11] used a finite-volume code and the SIMPLE scheme to study the transport and deposition of nanoparticles in a rotating curved pipe for different angular velocities, Dean number and Schmidt number. The results show that when the Schmidt number is low, the nanoparticle distributions are mostly determined by the axial velocity. When the Schmidt number is many orders of magnitude higher than 1, the secondary flow will dominate the nanoparticle distribution. When the pipe rotates, the distribution of nanoparticle mass fraction is similar to that for the stationary case. Penget al. [12] investigated the effect of nanoparticle on the frictional pressure drop characteristics inside a horizontal smooth tube. The results showed that the frictional pressured drop increases with the increase of the mass fraction of nanoparticles,and the maximum enhancement of frictional pressure drop is 20.8%. Lin and Lin [13] studied the nanoparticle transport and deposition in bends with circular cross-section. The results showed that the particle transport patterns are similar and independent of particle size and other parameters when suspended nanoparticles flow in a straight tube. At the outside wall, particle deposition is the most intensive, while it is the weakest at the inside wall. Laiet al. [14] presented the relative viscosity for gamma-Al2O3nanoparticles in water and propylene glycol-water mixture based on pressure drop measurements of fluid flow containing nanoparticles. The results indicated that with constant wall heat flux, the relative viscosities of fluid decrease with increasing volume flow rate, and the viscosity can be explained in part by the aspect ratio of the aggregates. Qianet al. [15] investigated the motion of nanoparticles with the laser speckle velocimetry technique. It is found that the overall motion of nanoparticles was along the pipe flow direction. To a small extent,however, nanoparticle motion vectors deviated from the axial direction, and the deviations were random because of the Brownian motion of nanoparticles.

Most of the studies mentioned above are focused on the effects of nanoparticles on the pressure drop and effective viscosity, or the deposition properties.However, the dynamic evolution due to nanoparticle coagulation is an important phenomenon and particularly interesting in applications. Nanoparticle coagulation will result in the variation of particle number concentration, particle cluster diameter and particle polydispersity along the radial direction in the pipe,which has not been found in the literature. Therefore,the present study investigates the evolution of particle number concentration, total particle mass, polydispersity, particle cluster diameter and geometric standard deviation considering the particle coagulation and dispersion in a pipe for different Schmidt numbers and Damköhler numbers with the moment method.

There are in general three approaches for simulating flows which contain the nanoparticles: the moment method, the Lagrangian method, and the discrete/sectional method. The moment method is based on the idea that the properties of interest can be determined from average measures of the properties of individual particles [16]. In the present study, this moment method is used because it requires a reduced set of additional transport equations, thus reducing the computational cost. Settumba and Garrick [17] performed a numerical simulation of nanoparticle coagulation in a temporal mixing layerviaa moment method, while the present study investigates nanoparticle migration in a fully developed turbulent pipe flow considering the particle coagulation.

2 MATHEMATICAL FORMULATION

Fluid containing nanoparticles flows from left to right through the pipe as shown in Fig. 1. The fluid flow is considered as steady-state and fully developed turbulent, and the mean velocity profile can be given as [18]

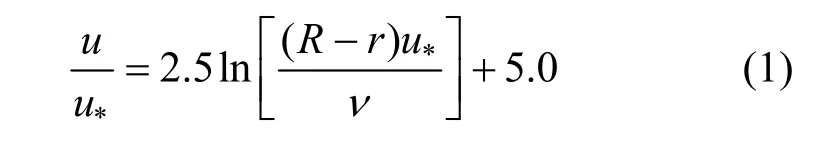
whereuis the flow velocity,*uis the friction velocity,νis the fluid kinematic viscosity,Randrare shown in Fig. 1.

Figure 1 Pipe flow and the coordinate system

The nanoparticles undergo diffusion and coagulation in turbulent flow, and their clustering is governed by the general dynamic population balance equation [19]:

wheren=n(v,x,t) is the particle size distribution function based on cluster volume,ujis the flow velocity,Dis the coefficient of diffusivity,βis the collision coefficient which is dependent on particle size,vandvare the two classes of particles of volumes. On the left-hand side of Eq. (2) the first term is the time rate of change of particle concentration and the second term represents the fluid transport. On the right-hand side the first term is the diffusion of particle, the second term represents the production rate of particles of volumevby collision of particles of volumesv, and the third term gives the disappearance rate of particle cluster having volumevby collisions with particles of all sizes.

A moment method is employed to obtain the moments of the nanoparticle distribution using the solution of the general dynamic equation. The general moment of the nanoparticle distribution function,Mk,is defined as:vvand

wherekis the order of the moment. Then the number of particles, dN, per unit volume of gas at a given position in space and time in the particle volume ranging from v to v+dv is dN=n(v, t)dv, and the volume of particles, dV, per unit volume of gas in the particle volume ranging from v to v+dv is dV=vn(v, t)dv.Therefore, the zero moment is:

另一方面，本文也认为，喜欢迁移因而在多个地域留下后代的古人，也就在不同地区留下了他的基因，当一个地区发生突然毁灭性的灾变时，其他地方的基因能得以流传。也许这种事件发生的概率很小，但考虑到进化时间的漫长，这种看似微不足道的细小差异在大浪淘沙的漫长人类演进旅途中，由于其初始条件的敏感性，这种生存优势会起到重要的作用。所以喜欢迁移的古人繁殖、生存的机会更多。反之，由于自然选择的作用，不喜欢移动的古人的基因则比较容易湮灭。

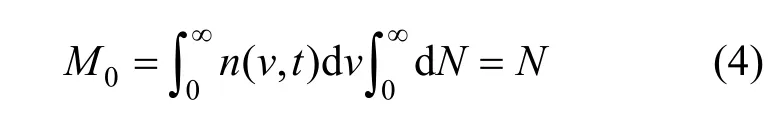
which represents the cumulative particle number distribution and is the total concentration of particles of all volumes at a given point. The first moment is

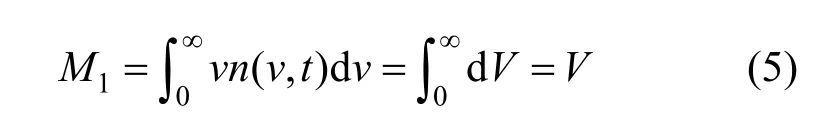
which represents the total volumes of particles of all volumes, and is proportional to the total particle mass for a definite particle density. The second moment is proportional to the light scattering by particles when they are much smaller than the wavelength of the incident light. A non-dimensionalized transport equation for the kth moment Mkis expressed as [17]

In the present study, a unimodal lognormal particle size distribution is used [17]:

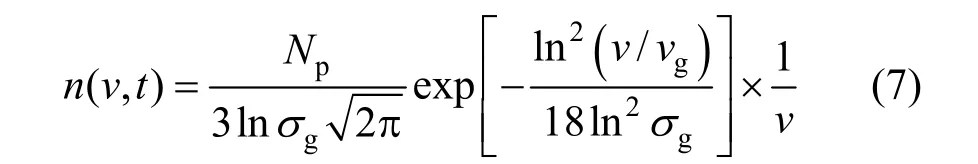
where Npis the total particle number concentration; vgand σgare the geometric mean volume and standard deviation, respectively, and they are expressed as [20]

where kBis the Boltzmann constant, T is the fluid temperature, ρgis the gas density,c and β are the mean thermal speed and accommodation coefficient,respectively. The fractional moment appearing in Eq.(6) is given by [20]

The source termkMω˙ in Eq. (6) is expressed as [17]

where L is the characteristic length scale, i.e., pipe diameter, Φ is the initial particle volume fraction,g,0v is determined by substituting,0kM into Eq. (8), the collision frequency A1is

3 RESULTS AND DISCUSSION

3.1 Validation of computation code and numerical parameters

The computation grid is comprised of 40(r)×50(θ)×80(z)=160000 grid points in a cylindrical coordinate system as shown in Fig. 1. We made a computing program to solve above equations. The extensive tests and refinements of the independence and suitability of the grid size for the convergence results were performed, i.e., the relative difference between the numerical results of M0and M1for different grid resolution are less than 10-3when changing grid points from 30 to 50 in axial direction, 40 to 60 in circumferential and 70 to 90 in radial direction, respectively. The tests were performed with 50 time step.

In order to validate the computation methods and codes, the numerical particle concentration distribution along the radial direction in the present study is compared with that given by Ding and Wen [6] as shown in Fig. 2. It can be seen that the two results are in agreement.

Figure 2 Comparison of particle concentration distribution at Re=15000● present simulation; ■ Ding and Wen’s numerical simulation [6]

The fluid is gas atT=293 K with the viscosityνand the densityρof 15×10-6m2·s-1and 1.205 kg·m-3,respectively. The flow Reynolds number is 15000. The Boltzmann constantkBis 1.38×10-23J·K-1, the mean thermal speedcis 500 m·s-1, the accommodation coefficientβis 0.9 [20]. The dimensionless time step Δtis kept constant as 0.05, which is 0.1 s. The flow is initially populated with the particles ofdp=1 nm(correspondingScM3.17) within the whole pipe. As the particle is initially monodisperse, the geometric standard deviation is initialized toσg,0=1, and each initial particle volume isv=π / 6 × 1 0-27m3. The

g,0

reference values of moments are determined byM0,0=Φ/vg,0,M1,0=ΦandM2,0=Φ×vg,0. The Damköhler numberDais kept to be 1. The values of other parameters are listed in Table 1. Eq. (6) is solved using an explicit finite difference scheme which is first order accurate in time and second order accurate in space. The zero gradient boundary conditions are applied to the walls. Distributions of particle parameters are symmetric about the pipe center line, so only distributions in half cross-section are given.

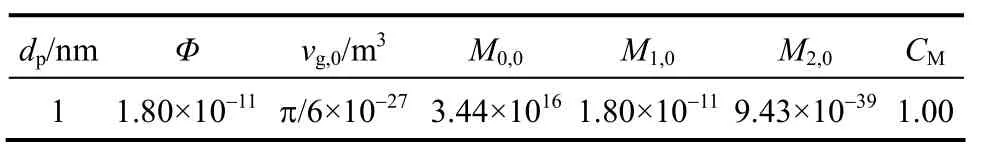
Table 1 Initial parameters

3.2 Evolution of particle number concentration

Figure 3 Evolution of particle number concentration along the radial direction with time (ScM=3.17 and Da=1)■ t=0 s; ● t=10 s; ▲ t=16 s; ▼ t=22 s; ◆ t=30 s

The distribution of particle number concentration is affected by the particle coagulation and diffusion induced by Brownian motion and shear flow. The evolution of particle number concentration along the radial direction with time is shown in Fig. 3. A non-uniform distribution of particle number concentration is seen along the radial direction,i.e., the particle number concentration is larger than the initial value in the region from the pipe center tor/R=0.4,but less than the initial value in the region fromr/R=0.4 to the wall. This means that particles move to the pipe center. This phenomenon becomes more obvious as time goes by. The non-uniformity is mainly because of the stronger contributions of the shearinduced particle migration than that of the Brownian motion. The net result of the Brownian motion is redistribution of particles between higher concentration regions to lower concentration regions, which exhibits as diffusion. The particles in the regions near the wall undergo large shear-induced force because there exists larger velocity gradient. On the one hand, migration of particles to the pipe center makes the increase of particle number concentration. On the other hand, particle coagulation makes the decrease of particle number concentration. The net result of these two mechanisms makes the increase of particle number concentration as shown in Fig. 3 because the value of particle number concentration is larger than the initial value in the region from the pipe center tor/R=0.4. The particle number concentration in the region fromr/R=0.4 to the wall is less than the initial value because some particles move to the pipe center, and other particles coagulate. Lamet al. [22] investigated particle migration in concentrated suspensions of micro-sized particles, and found that particle concentration was the lowest at the wall, rapidly increased to the maximum atr/R～0.8-0.9, but decreased slightly towards the pipe center. Therefore, the migration properties for nano-sized particles are different from that for micro-sized particles.

3.3 Evolution of total particle mass

Figure 4 Evolution of total particle mass along the radial direction with time (ScM=3.17 and Da=1)■ t=0 s; ● t=10 s; ▲ t=16 s; ▼ t=22 s; ◆ t=30 s

The radial variation of total particle mass at different times is shown in Fig. 4. In the present study no particle deposition is assumed, hence the total particle mass in the flow is conserved. A non-uniform distribution of total particle mass along the radial direction is obvious. The total particle mass increases from the wall to the pipe center. The non-uniformity tends to be obvious as time goes by, and the total particle mass in the whole flow remains unchanged even though the particles number concentration and particle diameter will change because of particle coagulation. Particles move to the pipe center, which results in an increase of total particle mass in the region from the pipe center tor/R=0.4 and a decrease in the region formr/R=0.4 to the wall. Total particle mass consists of flow velocity and mass density distribution. The flow velocity has a larger effect on the total particle mass because the total particle mass is proportional to the flow velocity while initial mass density distribution is homogeneous.

3.4 Evolution of particle diameter

Particle coagulation results in the growth of the particle cluster, which is quantified by the particle diameterdp:

thendp=(M1/M0)1/3nm.

In an initially monodisperse particle field, coagulation will produces particles of various sizes and increases the size of each particle. As the coagulation proceeds, therefore, particle diameter will increase throughout the flow domain. Fig. 5 shows the variation of the particle diameter along the radial direction. As time goes by particle diameterdpgrows from an initial value of 1 to the different values depending on the radial position. The largest particles are found in the pipe center because the migration of particles to the pipe center may encourage coagulation due to higher local concentration. These coagulated particles are less likely to be broken due to low shear rate in the region near the pipe center.

Figure 5 Evolution of particle diameter along the radial direction with time (ScM=3.17 and Da=1)■ t=0 s; ● t=10 s; ▲ t=16 s; ▼ t=22 s; ◆ t=30 s

3.5 Effect of Schmidt number on the particle number concentration and total particle mass

The Schmidt numberScMrepresents the ratio of the gas molecular diffusion to the particle diffusion. In the present study, the related parameters are constant for gas, soScMis determined only by the particle diameterdp. Assumed that the flow is initially populated withdp=1, 1.5 and 2 nm within the pipe cross-sections,then the corresponding Schmidt numbersScMare 3.17,7.13 and 12.68, respectively. The geometric standard deviation is initialized toσg,0=1, and each initial particle volumevg,0is π/6×10-27, and 4π/3×10-27m3fordp=1, 1.5 and 2 nm, respectively. When the effect ofScMis considered,Dais kept to be 1, the initial particle volume fractionΦis approximately 1.8×10-11,5×10-11and 10-10fordp=1, 1.5 and 2 nm, respectively, based onDain Eq. (14). The values of other initial parameters are listed in Table 2.

Figures 6 and 7 show the distribution of particle number concentration and total particle mass along the radial direction att=30 s with different Schmidt numbers. It can be seen that the particle number concentration and total particle mass decrease with the increase ofScMin the region near the pipe center. Thereason is that sinceScMrepresents the ratio of the gas molecular diffusion to the particle diffusion, largerScMcorresponds to the smaller particle diffusion,i.e.,fewer particles move to the pipe center. Besides, the collision frequency is inversely proportional to the particle inertial as shown in Eq. (16),i.e., probability of coagulation is less for large particles than for small particles, so that the nanoparticles with lower Schmidt number correspond to many different cluster sizes,i.e.more polydispersity.

Table 2 Initial parameters

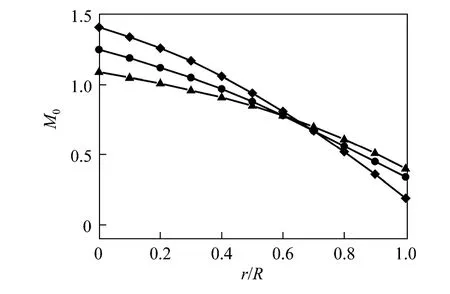
Figure 6 Effect of Schmidt number on the particle number concentration at t=30 s (Da=1)◆ ScM=3.17; ● ScM=7.13; ▲ ScM=12.68

Figure 7 Effect of Schmidt number on total particle mass at t=30 s (Da=1)◆ ScM=3.17; ● ScM=7.13; ▲ ScM=12.68

Table 3 Initial parameters

3.6 Effect of Damköhler number on the particle diameter and geometric standard deviation

IfScMis kept to be 3.17 for the particles withdp=1 nm, then the initial particle volumevg,0is π/6×10-27m3. The values of other parameters are listed in Table 3.

Effect of the Damköhler number can be quantified by considering the radial distribution of the moment variables att=30 s forDa=0.5, 1 and 2. Fig. 8 shows the distribution of particle diameter along the radial direction att=30 s for different Damköhler numbers. It can be seen that the particle diameter increases with the increase ofDaat the same radial position. For three different Damköhler numbers the particle diameter decreases slightly from the pipe center to the wall, which illustrates that larger particles accumulate near the pipe center. The effect of Damköhler number on the geometric standard deviation is shown in Fig. 9. We can see that the geometric standard deviation also grows with the increase ofDaat the same radial position. The increase in geometric standard deviation reveals that there is increased difference in particle diameter because of the particle coagulation.

Figure 8 Effect of the Damköhler number on the distributions of particle diameter at t=30 s (ScM=3.17)● Da=0.5; ◆ Da=1; ▲ Da=2

Figure 9 Effect of the Damköhler number on the geometric standard deviation at t=30 s (ScM=3.17)● Da=0.5; ◆ Da=1; ▲ Da=2

4 CONCLUSIONS

Evolution of particle number concentration, total particle mass, particle diameter and particle polydispersity considering particle coagulation and dispersion in a fully developed turbulent pipe for different Schmidt numbers and Damköhler numbers is studied with the moment method. The results show that particles move to pipe center and particle number concentration distributes non-uniformly along radial direction,which becomes more obvious as time goes by. The migration property for nano-sized particles is different from that for micro-sized particles. A non-uniform distribution of total particle mass along radial direction is also obvious. Total particle mass increases from the wall to the pipe center. The non-uniformity tends to be obvious. In an initially monodisperse particle field, coagulation will produces particles of various sizes and increases the size of each particle. As time progresses, particle diameter grows from an initial value to the different values depending on the radial position. The largest particles are found in the pipe center. Particle number concentration and total particle mass decrease with the increase of Schmidt number in the region near the pipe center. Probability of coagulation is less for large particles than for small particles so that the particles with lower Schmidt number are of many different sizes,i.e. more polydispersity. Particle diameter and geometric standard deviation increase with the increase of Damköhler number at the same radial position. Increase in geometric standard deviation reveals that there is increased difference in particle diameter because of the particle coagulation.

NOMENCLATURE

Φinitial particle volume fraction

1 Kittelson, D.B., “Engines and nanoparticles: A review”,J.Aerosol Sci., 29, 575-588 (1998).

2 Yu, M.Z., Lin, J.Z., Chen, L.H., Chan, T.L., “Large eddy simulation of a planar jet flow with nanoparticle coagulation”,Acta Mech.Sinica, 22 (4), 293-300 (2006).

3 Chan, T.L., Lin, J.Z., Zhou, K., Chan, C.K., “Simultaneous numerical simulation of nano and fine particle coagulation and dispersion in a round jet”,J.AerosolSci., 37, 1545-1561 (2006).

4 Yu, M.Z., Lin, J.Z., Chan, T.L., “Numerical simulation of nanoparticle synthesis in diffusion flame reactor”,Powder Technology, 181,9-20 (2008).

5 Yu, M.Z., Lin, J.Z., Chan, T.L., “Effect of precursor loading on non-spherical TiO2nanoparticle synthesis in a diffusion flame reactor”,Chem.Eng.Sci., 63, 2317-2329 (2008).

6 Ding, W.L., Wen, D.S., “Particle migration in a flow of nanoparticle suspension”,Powder Technol., 149, 84-92 (2005).

7 Jiang, S.P., Lee, J.H., Hwang, K.S., Choi, S.U.S., “Particle concentration and tube size dependence of viscosities of Al2O3-water nanofluids flowing through micro- and minitubes”,Appl.Phys.Lett., 91,243112 (2007).

8 Akbarinia, A., Behzadmehr, A., “Numerical study of laminar mixed convection of a nanofluid in horizontal curved tubes”,Appl.Therm.Eng., 27, 1327-1337 (2007).

9 Mirmasoumi, S., Behzadmehr, A., “Numerical study of laminar mixed convection of a nanofluid in a horizontal tube using two-phase mixture model”,Appl.Therm.Eng., 28, 717-727 (2008).

10 Jwo, C.S., Teng, T.P., Wu, D.J., Chang, H., Chen, S.L., “Research on pressure loss of alumina nanofluid flow in a pipe”,J.Chinese Soc.Mech.Eng., 30, 511-517 (2009). (in Chinese)

11 Lin, J.Z., Lin, P.F., Chen, H.J., “Research on the transport and deposition of nanoparticles in a rotating curved pipe”,Physi.Fluids, 21,122001 (2009).

12 Peng, H., Ding, G.L., Jiang, W.T., Hu, H.T., Gao, Y.F., “Measurement and correlation of frictional pressure drop of refrigerant-based nanofluid flow boiling inside a horizontal smooth tube”,Int.J.Refrig.Revue Int.Du Froid, 32, 1756-1764 (2009).

13 Lin, P.F., Lin, J.Z., “Prediction of nanoparticle transport and deposition in bends”,Appl.Math.Mech.Eng.Ed., 30, 957-968 (2009).

14 Lai, W.Y., Phelan, P.E., Prasher, R.S., “Pressure-drop viscosity measurements for gamma-Al2O3nanoparticles in water and PG-water mixtures (nanofluids)”,J.Nanosci.Nanotechnol., 10, 8026-8034 (2010).15 Qian, M., Yan, Q., Ni, X.W., Zheng, H.R., “Detection of nanoparticle Brownian motions in a nanofluid using laser speckle velocimetry”,Lasers Eng., 20, 117-128 (2010).

16 Wright, D.L., Yu, S.C., Shaocai, Y., Kasibhatla, P.S., McGraw, R.,Schwartz, S.E., Saxena, V.K., Yue, G.K., “Retrieval of aerosol properties from moments of the particle size distribution for kernels involving the step function: Cloud droplet activation”,J.AerosolSci.,33, 319-337 (2002).

17 Settumba, N., Garrick, S.C., “Direct numerical simulation of nanoparticle coagulation in a temporal mixing layerviaa moment method”,J.AerosolSci., 34, 149-167(2003).

18 Hinze, J.O., Turbulence, McGraw-Hill, USA (1975).

19 Friedlander, S.K., Smoke, Dust and Haze: Fundamentals of Aerosol Behavior, Wiley, New York (2000).

20 Pratsinis, S.E., “Simultaneous nucleation, condensation and coagulation in aerosol reactors”,J.Colloid Interface Sci., 124, 416-427(1988).

21 Suh, S.M., Zachariah, M.R., Girshick, S.L., “Numerical modelling of silicon oxide particle formation and transport in a one-dimensional low-pressure chemical vapor deposition reactor”,J.Aerosol Sci., 33(6), 943-959 (2002).

22 Lam, Y.C., Chen, X., Tan, K.W., Chai, J.C., Yu, S.C.M., “Numerical investigation of particle migration if Poiseuille flow of composite system”,Composites Science and Technology, 64, 1001-1010 (2004).