A Geometric Approach to Support Vector Regression and Its Application to Fermentation Process Fast Modeling*

WANG Jianlin (王建林)**, FENG Xuying (冯絮影) and YU Tao (于涛)

College of Information Science and Technology, Beijing University of Chemical Technology, Beijing 100029, China

1 INTRODUCTION

The soft-sensor techniques and optimal control techniques have been widely applied to monitor and control fed-batch bioreactor for fermentation processes[1, 2]. Their limitation is the existence of model-plant mismatches, which is an important issue in model-based techniques, so it is necessary to improve the model via on-line remodeling. However, the process data may be a large set after many runs of a fed-batch fermentation process. Fast modeling method based on large process dataset, therefore, is a challenge task.

Support vector machine (SVM) is a powerful machine learning method based on the statistical learning theory (SLT) [3, 4], and has been widely applied to solve classification and regression problems.SVMs have recently attracted much attention because of its many advantages over other approaches: (1)uniqueness of the solution, (2) good generalization of the solution, (3) rigid theoretical foundation based on SLT and optimization theory, (4) common formulation for the class separable and the class non-separable problems as well as for linear and non-linear problems,(5) clear geometric intuition of the classification problem, etc. For SVM classification (SVC) problems,SVMs attempt to optimize the generalization bound by separating data with a maximal margin classifier,which can be formulated as a quadratic programming problem (QPP) in the Wolfe dual representation. Although there exist many methods for solving QPPs,most mathematical programming approaches require enormous matrix storage and intensive matrix operations, which limit the large-scale SVM applications.Solving large-scale SVMs becomes one of the most important problems.

Fortunately, the special structure of the SVM optimization problem permits a class of specially tailored algorithms. The main stream of solving methods is algebraic, mainly based on decomposition and analytical methods [5]. One of the most well-known algebraic algorithms is sequential minimal optimization(SMO) [6, 7], which combines speed and ease of implementation with very good scalability. Another idea to solve SVM problem is geometric, based on the geometric interpretation. Geometrically, SVC problem is equivalent to solve a nearest point problem (NPP)between two convex sets, to find the nearest points in the (reduced) convex hulls of the data from each class,and the points with the minimum distance from the hyperplane are called support vectors. The linear requirement in memory storage allows geometric algorithms to be applied in large-scale problems.

The first geometric interpretation of SVCs can be traced back to the work of Bennett and Bredensteiner[8], and many important geometric ideas have subsequently appeared [9, 10]. All these geometric explanations provide a very intuitive background for the understanding and the solution of many problems in the fields of pattern recognition and machine learning. By using a modified kernel technique, an inseparable SVC problem with L2-norm penalty can be transformed into a separable one [10]. Most popular SVMs, such as c-SVM [11] and ν-SVM [12], are based on L1-norm penalty functions. Many researchers have argued that L1-norm SVMs have real advantage over L2-norm SVMs, especially when the redundant noise features are considered [13]. Fortunately, SVMs with L1-norm penalty are geometrically interpreted with the reduced convex hulls (RCHs) [8, 9]. Tao et al. have successfully presented a general technique for developing corresponding geometric algorithms (i.e., Gilbert, MDM,SK, etc.) for L1-norm penalty SVCs training [14, 15].

Although there are some efficient geometric algorithms for training SVMs, almost all the algorithms introduced are only suitable for SVC designs. Bi and Bennett [16] regard an SVR as a classification problem in the input space, and use a geometric algorithm to solve the problem. However, their method is just suitable for training a kind of modified ε-SVM, and is incapable of training other SVMs.

In this paper, a geometric interpretation for both L2-norm and L1-norm penalty SVRs is derived. The geometric algorithms developed for the SVC is applicable to the SVR. A geometric approach, Gilbert algorithm,is extended to train SVR, and the experimental results of fermentation process modeling show its efficiency.

2 GEOMETRIC APPROACH TO SVM

2.1 The geometric representation of SVC

Pattern recognition is a very active field of research intimately bound to machine learning. SVC is a modern machine learning method that has given superior results in various classification and pattern recognition problems. The primal SVM finds the generalized optimal separating hyperplane with maximum hard margin between two sets. This idea can be implemented by the structural risk minimization (SRM)principle [3, 4].convenience. Since the algorithms update the nearest point in inner product form, the simplified expressions do not affect their application in kernel form.

Table 1 SVC problems with different penalty functions and the correspondingWolfe-dual problems with the regularization parameters C＞0 and v＞0

Table 2 SVR problems with different penalty functions and the corresponding Wolfe-dual problems with the regularization parameters C＞0 and v＞0, and step(x) = [ 1 + s ign(x )]/2 in the Huber loss function of Huber-SVR

Figure 1 Gilbert algorithm for μ-SVM regression

The modified geometric algorithm is described in above pseudo-code just for the convenience of algorithm understanding. In fact, some other efficient strategies can be used, such as inner product caching. By caching allwhere ∀xi∈Xwith non-zero coefficient,the algorithms can be speeded up substantially. Applying geometric algorithm in regression problem needs to duplicate the dataset double formally, but it does not require to search the dataset twice in each iteration. In each loop in geometric algorithm,can be calculated synchronously by searching the dataset just once. This means that the geometric algorithm for SVR theoretically has almost the same computational complexity as it for SVC.

Although there are other geometric algorithms based on different strategies, such as SK [18, 19],MDM [20], and nearest point algorithm (NPA) [10],they are all found on the inner product computation of training data. That makes our approach convenient to be applied in different geometric algorithms.

3 RESULTS AND DISCUSSION

In this section, some experiments of process modeling are conducted to verify the theoretical analysis ofμ-SVM regression. Since SMO algorithm is currently one of the fastest algebraic algorithms for SVM design, the modified geometric algorithms are expected to have comparisons against SMO in terms of computational cost. In each iteration step of these algorithms, the number of kernel function evaluation is major cost rather than other operations, so the total computational cost approximately depends on the convergence rate and kernel evaluations in each loop.Our algorithms are implemented in MatlabTM.

The datasets are acquired for 18 rounds from a fed-batch fermentation process, and each run lasts 120 h with sampling interval 30 min. In all the experiments, Gaussian kernelwith 0.5σ= is used.μ-SVM with 0.2μ= is trained by geometric algorithms, andv-SVM with 2/vmμ=is trained by SMO for equipollence.

The predictive profiles based on the results of fermentation process modeling are shown in Fig. 2.Both of the Gilbert and SMO algorithms perform well.

Figure 2 The comparison results of two algorithms for fermentation process modeling SMO; Gilbert

As potential methods for solving large-scale SVM, the geometric algorithms have comparisons against algebraic algorithms in terms of computational cost. The quantitative comparison against SMO algorithms in terms of the averaged CPU times is shown in Fig. 3. Although the algorithms are initialized randomly, the result illustrates that the geometric algorithm is better than SMO algorithm in this case.

4 CONCLUSIONS

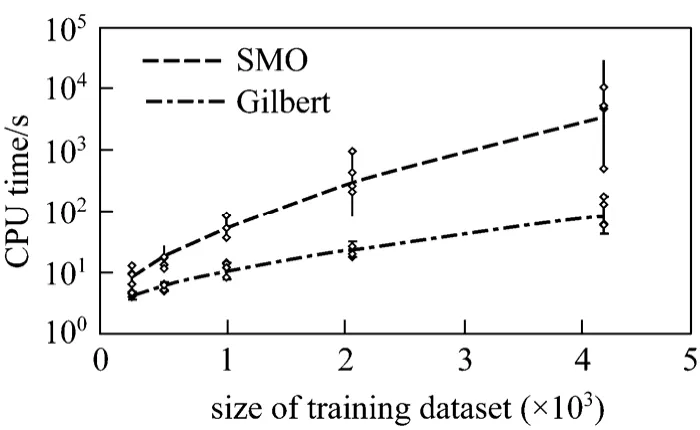
Figure 3 The relation between averaged CPU time and size of datasets

In this paper, it is shown that SVR problems can be represented as a NPP in feature space. Theμ-SVM method is applied successfully to solve regression problem, which could be bothL1-norm andL2-norm penalty. Almost all the available geometric algorithms for SVC training can be modified to solve SVR problems. Theμ-SVM method is applied to a real-world fermentation process modeling, and the experimental results show that the geometric algorithm performs better than SMO coded in MatlabTM.

Since the algorithms in this work are implemented in MatlabTMand not optimized much, the performance of fine tuned version algorithms can be improved further. More specific and practical SVM algorithms for large scale applications and the geometric methods for nonstandard SVMs will be investigated in the future study.

NOMENCLATURE

1 Chen, L.Z., Nguang, S.K., Chen, X.D., Li, X.M., “Modeling and optimization of fed-batch fermentation processes using dynamic neural networks and genetic algorithms”,Biochem.Eng.J., 22 (1), 51-61(2004).

2 Trelea, I.C., Titica, M., Landaud, S., Latrille, E., Corrieu, G., Cheruy,A., “Predictive modeling of brewing fermentation: from knowledge-based to black-box models”,Math.Comput.Simulat., 56,405-424 (2001).

3 Vapnik, V.N., Statistical Learning Theory, Wiley, New York (1998).

4 Vapnik, V.N., The Nature of Statistical Learning Theory,Springer-Verlag, New York (2000).

5 Osuna, E., Freund R., Girosi, F., “Improved training algorithm for support vector machines”, In: Proceedings of IEEE NNSP’97, Principe, J., Gile, L., Morgan, N., Wilson, E., eds., IEEE Press, New York, USA, 276-285 (1997).

6 Platt, J.C., “Fast training of support vector machines using sequential minimal optimization”, In: Advances in Kernel Methods-Support Vector Learning, Schölkopf, B., Burges, C.J.C., Smola, A.J., eds.,MIT Press, Cambridge, MA, USA, 185-208 (1999).

7 Keerthi, S.S., Shevade, S.K., Bhattacharyya, C., “Improvements to Platt’s SMO algorithm for SVM classifier design”,Neural Comput.,13 (3), 637-649 (2001).

8 Bennett, K.P., Bredensteiner, E.J., “Duality and geometry in SVM classifiers”, In: Proceedings of the 17th International Conference on Machine Learning, Langley, P., ed., Morgan Kaufmann Publishers,San Francisco, CA, USA, 57-64 (2000).

9 Crisp, D.J., Burges, C.J.C., “A geometric interpretation ofv-SVM classifiers”, In: Advances in Neural Information Processing Systems 12, Solla, S.A., Leen, T.K., Müller, K.R., eds., MIT Press, Cambridge, MA, USA, 244-251 (2000).

10 Keerthi, S.S., Shevade, S.K., Bhattacharyya, C., Murthy, K.R.K., “A fast iterative nearest point algorithm for support vector machine classifier design”,IEEE Trans Neural Networks, 11 (1), 124-136(2000).

11 Cortes, C., Vapnik,V., “Support vector networks”,Mach.Learn., 36,1991-1996 (2003).

12 Schölkopf, B., Smola, A.J., Williamson, R.C., Bartlett, P.L., “New support vector algorithms”, Neural Comput., 12, 1207-1245 (2000).

13 Zhu, J., Rosset, S., Hastie, T., Tibshirani, R., “1-norm support vector machines”, In: Advances in Neural Information Processing Systems 16, Thrun, S., Saul, L., Schòlkopf, B., eds., Neural Information Processing Systems Foundation (2003).

14 Tao, Q., Wu, G.W., Wang, J., “A generalized SK algorithm for learning v-SVM classifiers”, Pattern Recogn. Lett., 25 (10), 1165-1171(2004).

15 Tao, Q., Wu, G.W., Wang, J., “A general soft method for learning SVM classifiers with L1-norm penalty”, Pattern Recogn., 41,939-948 (2008).

16 Bi, J.B., Bennett, K.P., “A geometric approach to support vector regression”, Neurocomputing, 55, 79-108 (2003).

17 Gilbert, E.G., “An iterative procedure for computing the minimum of a quadratic form on a convex set”, SIAM J. Control, 4 (1), 61-79(1996).

18 Schlesinger, M.I., Hlaváč, V., “Ten lectures on statistical and structural pattern recognition”, Kluwer Academic Publishers, Dordrecht(2002).

19 Franc, V., Hlaváč, V., “An iterative algorithm learning the maximal margin classifier”, Pattern Recogn., 36, 1985-1996 (2003).

20 Mitchell, B.F., Dem’yanov, V.F., Malozemov, V.N., “Finding the point of a polyhedron closet to the origin”, SIAM J. Control, 12,19-26 (1974).