基于SPH方法的幂律流体突缩型管路流动过程仿真

刘 虎，强洪夫，韩亚伟，陈福振

（第二炮兵工程大学，陕西 西安710025）

0 引言

幂律型流体是指流变行为符合幂定律的流体，这类流体在石油工业、航空航天等领域应用较为广泛[1]。突缩型管路流动是指流体在管路中流动时，由于管路截面面积突然缩小而产生的流动现象[2]。对于火箭发动机而言，研究幂律型流体的突缩型管路流动特性，获取速度、剪切速率、粘度等的分布及变化情况，一方面可以为具有幂律型本构关系的推进剂的管路设计提供参考；另一方面，突缩型管路也可以看作喷注器喷口的简化形式。因此，对喷注器设计也具有一定指导意义。

光滑粒子流体动力学（Smoothed Particle Hydrodynamics,SPH） 方法是求解流体流动的一种无网格粒子法。由于流体粘性项中包含的速度的二阶导数很难求解，因此，早期SPH方法一般只用于求解Euler方程，即局限于非粘流动。目前，对于牛顿流体，较实用的方法是将有限差分方法与SPH方法相结合，将二阶导数降阶求解[3]；对于非牛顿流体，由于其本构关系种类较多，且关系式较为复杂，SPH方法的研究尚处于起步阶段[4-6]。

本文主要进行了以下工作：推导了广义流体动力学控制方程的SPH离散式，应用人工应力方法消除拉伸不稳定现象，应用XSPH方法规范粒子分布秩序，应用罚方法施加边界条件；提出了幂律型本构关系的SPH求解方法，推导了其计算公式；分别用本文方法及有限体积方法（Finite Volume Method,FVM）进行了Poiseuille流流动过程仿真，通过对比，证明了本文方法的正确性；将本文方法应用于幂律型流体的突缩型管路流动仿真研究，获得了管路流动特性，并与牛顿型流体（水）的流动特性进行了对比，分析了幂律型流体流动特性的成因。

1 SPH基本理论

1.1 控制方程及状态方程

本文采用的流体动力学控制方程为：

对于动量方程（2） 中的压力项p，采用弱可压缩状态方程进行求解：

式中：p0为参考压强；γ为常数，本文中取γ=7；p0和γ共同用于控制计算中流体密度在其常态密度附近的震荡幅度。

1.2 SPH基本方法及控制方程的离散

在SPH算法中，连续的流场离散成为一系列有相互作用的粒子，通过核函数估计技术在这些粒子上离散控制方程组，得到一组描述各粒子物理量随时间变化的常微分方程组，即SPH基本方程组，再对这组方程采用相应的常微分方程组求解方法来推进时间进程的求解。

式（1）-（3）的 SPH 离散式为：

式中：i，j为粒子编码；N为粒子i支持域内的粒子数；ρi为粒子i的密度；mj，ρj为粒子j的质量和密度；为核函数，它的选取直接影响计算的误差和稳定性，本文选用三次样条核函数；表示核函数对粒子i的偏导数；h为光滑长度，表示核函数不显著为零的取值范围，控制着SPH粒子的影响域。

式（7） 被称为XSPH方法，其基本思想是通过施加临近粒子的影响使自身的运动速度与临近粒子的平均速度相近，使粒子分布更加有序，消除由于分布不均匀带来的粒子的非物理聚集问题。 ξ(0≤ξ≤1)是一个常数，本文中ξ=0.3。

1.3 边界条件的施加

采用罚方法施加边界条件，边界力的计算方法为[8]：

1.4 时间积分

采用蛙跳 (Leap-frog)方法对SPH离散方程进行求解，它对时间是二阶精度，具有存储量低，计算效率高的特点。

式中：φ表示密度ρ及速度v； xi为粒子i的位置坐标。为了使计算过程稳定，采用考虑具有粘性耗散的时间步长表达式：

对于本文研究的幂律型流体而言，η为流体表观粘度。

2 幂律型本构关系的SPH处理

幂律型流体的本构关系式为：

流体的剪切速率可以表示为：

二维情况下，式（13）可写作：

对式（14）在粒子i处进行粒子估计：

式（15） 即为粒子i处剪切速率张量的SPH离散求解式。

借鉴牛顿流体中粘性的处理方法，本文应用下式来计算幂律型流体的粘性项：

当n<1时，

当η0取较大值时，式 （18） 可以代替式（17）近似描述幂律型流体的本构关系。

3 测试算例

应用Poiseuille算例验证第3节幂律型本构关系的SPH求解方法的正确性。Poiseuille流的模型为：流体在分别位于y=0和y=l的两块平行且无限大的固定平板间流动。初始静止的流体由于受到体力F（例如压力梯度或外力）的作用而在两平板间逐渐流动，最终达到稳定状态。

本算例中η0=106Pa·s，以近似表示式 （17）描述的幂律型流体本构关系。为增大时间步长，采用了较大尺寸的计算模型，其中，模型总体尺寸 0.4 m×0.4 m，粒子间距 0.01 m，粒子数 1 600，其中，流体粒子数1 520；边界粒子采用虚粒子，粒子数80。Poiseuille流模型的初始粒子分布如图1所示。

图1 Poiseuille流初始粒子分布图Fig.1 Initial particle distribution of Poiseuille flow

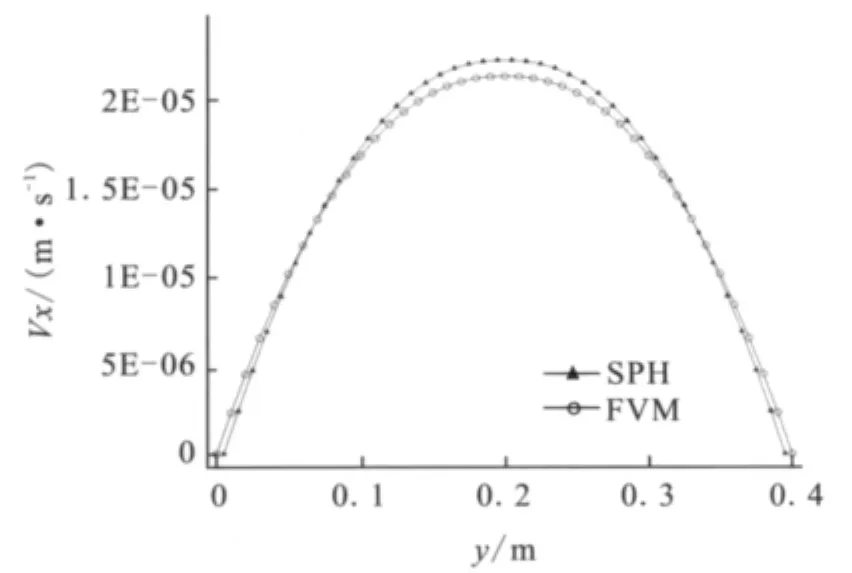
图2 Poiseuille流稳定时x=0处的速度分布图Fig.2 Velocity distribution of particles at x=0 when Poiseuille flow is stable

流体密度 ρ=1000 kg/m3。体力 F=2×10-4m/s2。流变指数n=0.8，稠度系数k=31.48 Pa·s。应用FVM方法对同等规模的网格模型进行了对比计算。图2为模拟达到稳定状态时，分别用SPH方法及FVM方法计算得到的x=0处的粒子速度分布图。由图2可以看出，SPH计算结果与FVM计算结果在速度变化趋势上完全一致，二者的最大相对误差为4.03%。

4 突缩型管路流动仿真

采用的突缩型管路模型如图3所示。推板以恒定的速度V=0.1 m/s推动管路内的流体向外流出，管路直径D=5.5×10-3m，管路截面面积与突缩口截面面积比Spipe/Sout=2，计算中不考虑重力作用。

图3 突缩型管路流动示意图Fig.3 Schematic of flow in sharply contractive pipe

模型粒子数5 552，其中，流体粒子5 000个，边界粒子552个；流体粒子间距1.1×10-4m，边界粒子间距5.5×10-5m。

采用牛顿型流体进行了突缩管路流动特性模拟，与幂律型流体的流动特性进行对比。牛顿型流体为水，幂律型流体的物质参数取自文献 [3]，其中，稠度系数k=41.65 Pa·s，流变指数 n=0.224，密度ρ=1000 kg/m3。结合文献 [3]中的表观粘度与剪切速率实验数据，取η0=0.3 Pa·s。

图4为突缩型管路流动仿真结果，通过对比可以发现，对于本算例，幂律型流体的流动特性与水有很大区别，表现为：

1） 相同时间内，幂律型流体的流动距离较小，流体液柱直径较大；

2）幂律型流体的液柱头部呈凸面形。

图4 突缩型管路流动仿真结果Fig.4 Simulation results of flow in sharply contractive pipe

图5突缩型管路流动的速度场变化过程Fig.5 Developing process of velocity field of flow in sharply contractive pipe

图5 为突缩型管路流动速度场的变化过程图，其中，上图为幂律型流体的速度变化过程图；下图为水的速度变化过程图。通过对比可以得出：

1） 各时刻的幂律型流体的流动速度均小于水流速度；

2） 流体自突缩口流出前（t＝0.00025 s），幂律型流体液速度呈凹面型，中间速度低，突缩口处速度高；流出后（t＝0.00225 s以后），呈凸面型，中间速度高，两侧速度低；水流速度始终表现为两侧速度高，中间速度低。

图6为幂律型流体液经过突缩型管路转角处的剪切速率分布等值线图。可以看出，流体的剪切速率值围绕突缩型管路转角呈环状分布，越靠近转角处，剪切速率值越大。

图6 幂律型流体经过突缩型管路转角处的剪切速率等值线图Fig.6 Isolines of shear rates while power-law fluid is flowing through the sharp edge of sharply contractive pipe

结合图4～图6，可以得到幂律型流体经过突缩型管路的流动特性成因：

1）由于幂律型流体的粘性远比水的粘性大，因此，幂律型流体在管路流动时受到的粘性阻力大，流动速度慢，在流量相同的情况下形成的液柱直径比水的液柱直径大；

2） 初始时刻，流体在推板的推动下向前运动，但并未通过突缩口，在突缩口转角处，两侧流体必须转向通过突缩口，导致速度急剧增大，此外，对于幂律型流体，速度的增大引起剪切速率变大，表观粘度减小，转角处受到的粘性阻力减小，同样引起速度的增大，因此，水和幂律型流体在喷注初期，突缩口截面的速度分布均呈凹面形，中间速度低，两侧速度高；

3） 流体从突缩口流出后，幂律型流体的粘度大，产生的粘性阻力大于牛顿型流体，导致幂律型流体的运动速度迅速减小，由于速度差主要存在于流体两侧，因此，两侧的减速作用尤为明显；此外，流体中间部分的流量比两侧流量大，也造成中间部分的流速比两侧流速高，从而导致幂律型流体的液柱头部形状及速度分布均呈凸面形。

5 结论

本文的方法可有效处理幂律型流体的本构关系。

幂律型流体的突缩型管路流动特性与水有很大差别，主要表现为流动阻力大、流速低、流动困难。

在本文研究范围内，粘性较大以及粘性随剪切速率的变化是形成幂律型流体流动特性的主要原因。

[1]NATAN B,RAHIMI S.The status of gel propellants in year 2000[C]//Proceedings of 5th International Symposium on Special Topics in Chemical Propulsion:Combustion of EnergeticMaterials.BocaRaton:BegelHouse,2000:1-24.

[2]张蒙正,左博．幂律型凝胶推进剂管路中的流动特性[J]．推进技术,2009,30(2):246-250．

[3]BASA M,QUINLAN N J,LASTIWKA M.Robustness and accuracy of SPH formulations for viscous flow[J].International Journal for Numerical Methods in Fluids,2009,60:1127-1148.

[4]FANG Jian-nong,OWENS R G,TACHER L,et al.A numericalstudyoftheSPH method forsimulating transient viscoelastic free surface flows[J].Journal of Non-Newtonian Fluid Mech,2006,139:68-84.

[5]RFIEE A,MANZARI M T,HOSSEINI M.An incom pressible SPH method for simulation of unsteady viscoelastic free-surface flows[J].International Journal of Non-Linear Mechanics,2007,42(10):1210-1223.

[6]FAN X J,TANNER R I,ZHENG R.Smoothed particle hydrodynamics simulation of non-Newtonian moulding flow [J].Journal of Non-Newtonian Fluid Mechanics,2010,165:219-226.

[7]MONAGHAN J J.SPH without a tensile instability[J].Journal of Computational Physics,2000,159:290-311.

[8]王坤鹏.基于接触边界条件SPH新方法及其工程应用[D].西安:第二炮兵工程大学201教研室,2008:25-29.