双局部行进波对流的高精度数值模拟

王 涛， 葛永斌

（1.北方民族大学预科教育学院，宁夏银川 750021；2.宁夏大学数学计算机学院，宁夏银川 750021）

0 引 言

早在1900年以前，Benard等人就进行了关于热浮力不稳定导致对流的实验研究，Rayleigh最早（1916年）进行了理论分析，给出了底部受热的静止流体层稳定性判别的无量纲参数［1］。20世纪以来，Rayleigh－Benard对流一直是研究非平衡系统稳定性、非线性动力学特性、空间形态及湍流形成机理的重要物理模型之一。对于混合流体（如水和酒精，He3与He4等）对流，温度场和浓度场的耦合效应会改变系统的稳定及分岔特性。垂直方向的温度梯度可以诱导一个浓度梯度，产生的现象被称作Soret效应，可用分离比φ来表示，φ的大小直接影响着分岔的形态与非线性特性。当φ＞0时系统是一个类似纯流体对流的超分岔。可是，当φ＜0时系统是一个不同于纯流体对流的亚分岔，其临界对流点比纯流体时大。因此，当温度梯度或瑞利数超过对流临界值之后，系统会过渡到强非线性大振幅的行进波对流状态。

φ＜0时的行进波对流斑图极大地吸引了研究者的兴趣。20世纪80年代，Bell实验室在He3与He4对流实验中，首次观测到行进波对流现象［2］，即对流涡卷的空间位置不是固定不变的，而是以一定的速度在对流腔体内传播。这引起了人们对这一系统极大的关注。实验揭示了许多行进波对流斑图，局部行进波就是其中一种，即在一定上、下壁面温度差的条件下，局部区域存在对流运动，而其他区域无对流存在。文献［3－4］获得了一种被称为局部行进波的对流图案。文献［5］结果表明在φ＝－0.47，Γ＝46条件下的矩形窄槽中，靠近两端壁的对流区域和中间区域的传导区域共存。文献［6］研究了局部行进波的稳定性形态、对流中脉冲部分的运动情况以及它们内在的扰动，实验说明局部行进波依赖于表示上下温度差特性的瑞利数。

在国内，对这一系统的研究始于20世纪末，研究主要是在数值模拟方面。文献［7－10］对长高比为46的封闭腔体内的混合流体对流进行了研究，发现了对传波（CPW）、双局部行进波（DLTW）、具缺陷的混合流体行进波对流斑图，探讨了具有强Soret效应的混合流体Undulation行进波对流斑图的动力学特性。文献［11］对混合流体Rayleigh－Benard对流的线性稳定性进行了分析。文献［12］给出了双流体流动中脉冲扰动的时空演化。所有这些模拟，都提供了比实验更详实的资料和信息。可是，这些数值模拟研究都采用了低阶精度的差分格式，但当瑞利数增大且腔体物理条件变得复杂时，要对腔体内流体的对流运动状态成功地进行模拟并得到较高精度的求解结果，势必对计算格式所采用的算法的求解效率及精确度提出更高的要求。文献［13］的数值模拟研究是采用有限元的方法。文献［14］采用了高精度的差分格式，给出了长腔体内局部行进波的稳定区间。但是用高精度差分格式数值模拟具中等强度的Soret效应的对流系统中，双局部行进波特性的研究报道很少。因此，本文基于描述对流系统的流体力学基本方程组的高精度数值模拟，研究φ＝－0.47的具有中等强度的Soret效应的对流系统中的双局部行进波特性，揭示双局部行进波的形成过程，并讨论其稳定性。

1 数学物理模型

1.1 基本方程组

考虑一个底部加热的四周为固壁的方腔内充满混合流体的物理模型。如果上部平板的温度保持常数，当下部平板的温度升高到某个临界数值时，在2个平板之间对流运动发生，如图1所示，水平放置的矩形腔体，长为Lx，高为d，记Γ＝Lx／d，一薄层双流体混合物封入矩形腔体之中，例如酒精与水的混合物的水平层，使流体处于一个均匀的重力场中，g＝－g ez，g为重力加速度，方向向下，ez表示z方向的单位矢量。上下板之间存在一个正的温度差ΔΤ＝Τhot－Τcold，由瑞利数Ra来表征。当Ra引发的浮力项超过了极限，对流运动就开始发生。这里认为对流如实验中观察到的一样，以整齐的平行滚动形式出现。平行对流运动的斑图（Pattern）随上下板之间的温度差的变化而变化。在正交的x、z轴所在的平面上描述二维对流运动。

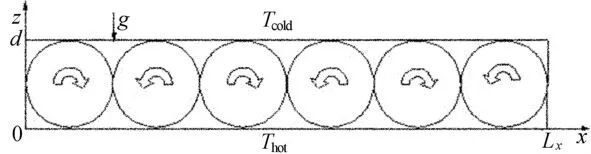
图1 对流模型示意图

对于这样的流动问题，可用二维流体力学方程组来描述。

假设坐标原点位于底板与左侧壁的交汇处，x轴向右为正，z轴向上为正。所有的几何尺寸用流体层厚度d表示，进行无因次化：时间t为d2／ν，速度U＊为ν／d，温度T＊为kν／（agd3），浓度，压力p为ν2／d2。考虑了Soret效应的流体力学基本方程组可表示为：

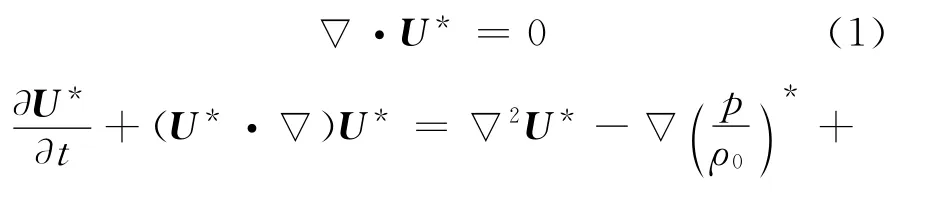
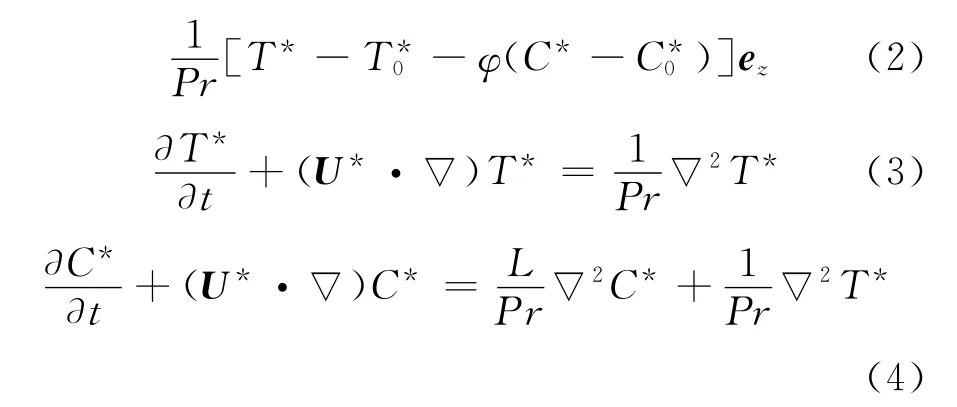
在Boussinesq近似假设下，T和C为温度和浓度离开参考值T0和C0一个小的偏差，质量密度ρ的状态方程可表示为：

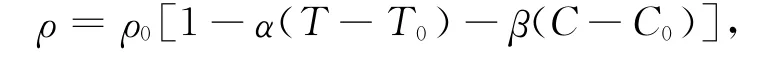
其中，ρ0为平均质量密度。

α的作用是单调的，因为不论液体或气体，温度升高时密度都会减小，α始终大于0；而β的作用却不一样，例如，随污染物质的增加，大气密度可能上升也可能下降。当β＜0时，对流系统类似于纯流体的情况，为定常流动；可是当β＞0时，对流系统会出现行进波状态、局部行进波及定常流动。α、β分别定义为：

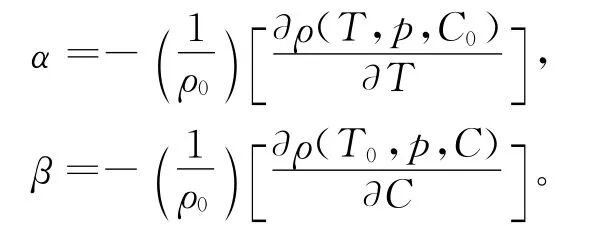
1.2 传导解

传导解可表示为：

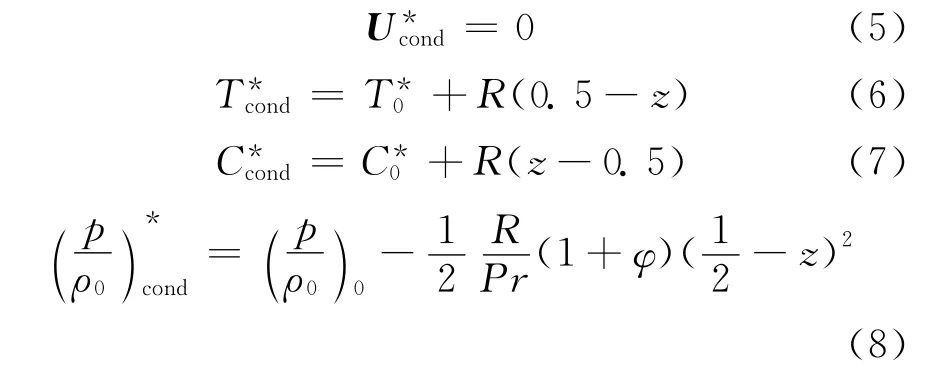
1.3 扰动方程组

进一步定义扰动量：

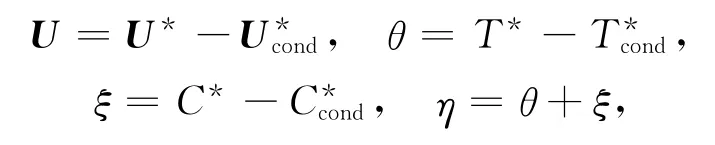
其中，U＝U（u，0，w）为扰动流速，u为水平方向的扰动流速，w为垂直方向的扰动流速；θ为扰动温度；ξ为扰动浓度；η为扰动浓度流束。

由方程（1）～（4）式和传导解（5）～（8）式，可得扰动方程组为：

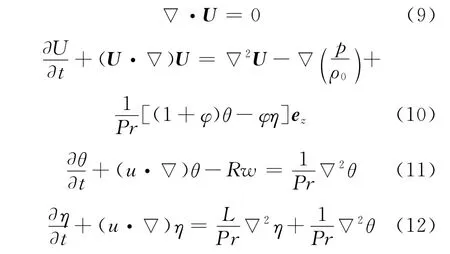
1.4 涡量－流函数形式的扰动方程组

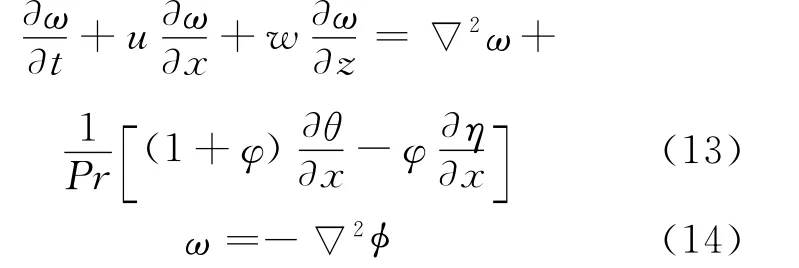
其中，（13）式为涡量输运方程，（14）式为流函数Poisson方程。

方程（11）～（14）组成了在Boussinesq假设下，二维非定常不可压缩二成分混合流体的涡量－流函数形式的基本控制方程组。

1.5 边界条件

为了求解方程组必须给出合理的边界条件。所有壁面都是固定的，速度在壁面上为0，浓度流束在壁面上是不可穿透的。

当z＝0，1时，u＝w＝∂w／∂z＝0，∂η／∂z＝0；

当x＝0，Γ时，u＝w＝∂w／∂x＝0，∂η／∂x＝0。

由于在上下边界上温度是固定的，温度的扰动量可表示为：

当z＝0，1时，θ＝0。

对于限定在矩形容器中的混合流体，容器是绝热的，故侧向边界条件可表示为：

2 高精度格式

在本文中，给出温度方程、浓度方程和涡量方程（11）～（13）式统一的表达形式：

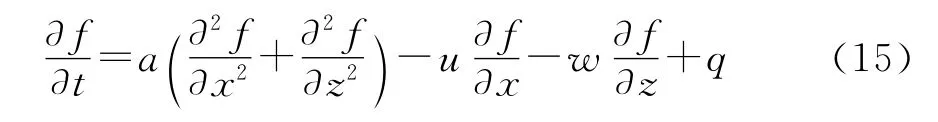
其中，f可表示ω、θ、η；q表示源项。

对于统一表达形式（15）式的求解，本文对时间方向采用三阶R－K公式［15］离散，在空间方向采用四阶精度的迎风格式［16］离散。

对流函数Poisson方程（14）式的求解，采用如下四阶紧致差分格式［17］：

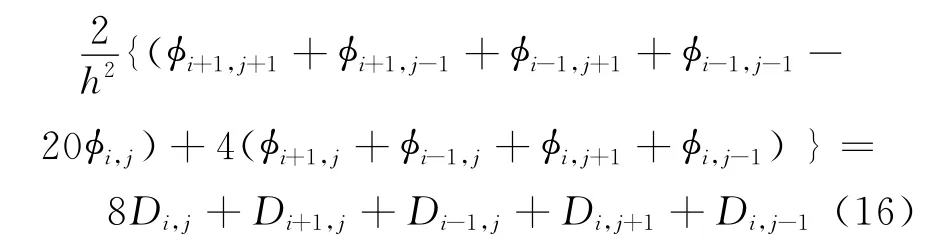
3 数值模拟及讨论

计算的初始条件为初始扰动波的波长为2倍的流体层厚度的平行滚动，其滚动的微小振幅的包络线为稍微偏离腔体中心的高斯分布函数，本文所模拟的是长高比为Γ＝46的空腔，初始扰动波的振幅在x＝25处达到最大值。这里给出初始扰动波的数学表达式为：

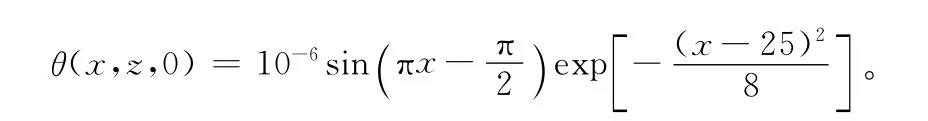
计算采用均匀网格Δx＝Δz＝1／10，时间步长为Δt＝5×10－4，计算中采用的其他流体参数分别取φ＝－0.47，Pr＝13.8，L＝0.01，这和文献［7］相同。为了方便，经常用相对瑞利数r表示，即r＝R／Rco，这里Rco是纯流体对流时的临界值（Rco＝1 708），R是混合流体对流时的瑞利数。从r＝2.10开始计算。

文献［14］中已用本文上述方法进行了计算，已说明本文方法能正确反映混合流体行进波对流运动情况。本文在选定的流体参数情况下，从相对临界瑞利数约为r＝2.10处开始计算，观察小扰动的成长。随时间增长，得到了稳定的ETW行进波状态，如图2所示。图2a给出了当r＝2.10值，腔体1／2高度处温度场随时间演化，时间从682.5～702.5，2条线间的间隔1.25，这与文献［5］所描述的ETW行进波状态也是一致的。

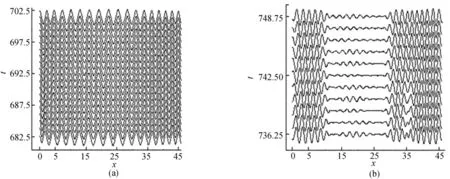
图2 r＝2.10时腔体1／2高度处扰动温度场随时间的演化

图2b给出了当r＝1.20值后，腔体1／2高度处温度场随时间演化，时间从736.25～748.75，2条线间的间隔1.25。由图2b可以发现，其中心行进波逐步向两边扩散，能量向两边界进行传递，中心区域逐步变成传导区域。

图3给出了当r＝1.23时，经过长时间的计算，腔体1／2高度处温度场随时间演化图，时间从806.25～813.25，2条线间的间隔1.25。从图3可以看出，得到了稳定的双局部行进波，行进波的前进方向是明显的，左侧壁（x＝0～10）和右侧壁（x＝30～46）附近的行进波宽度几乎保持常数，中间的传导区域（x＝10～30）随时间没有变化，其宽度保持为常数。左侧壁和右侧壁的行进波的宽度不相同，是因为在初始扰动温度，其滚动的微小振幅的包络线稍微偏离腔体中心。

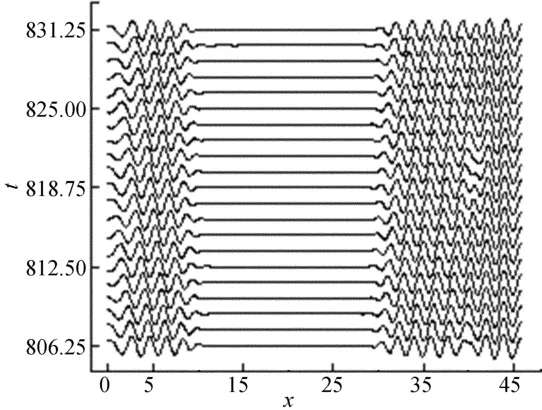
图3 r＝1.23时腔体1／2高度处扰动温度场随时间的演化

无量纲参数Nusselt数表示通过流体层的垂向热通量，用来表征温度场，平均Nusselt数被定义为。其中是传导状态的温度梯度，是一个常数；Γ为计算区域长度。

实际分析中计算了z＝0，1即下壁面（热壁）和上璧面（冷壁）的平均Nusselt数Nu0和Nu1。局部Nusselt数采用文献［18］的定义方式，即（θz）0，j的计算采用如下四阶精度的计算格式：

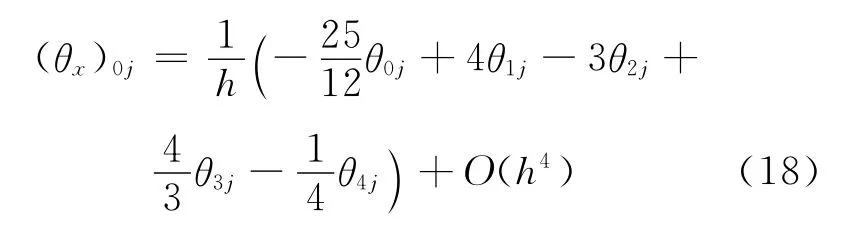
Nu0和Nu1的计算采用复合的Simpson公式。

图4给出了r＝1.23时，腔体在t＝806.25时刻下壁面（热壁）和上壁面（冷壁）的Nusselt数Nu0－1和Nu1－1，发现在两侧壁有行进波对流发生，中心区域则是无对流的传导区域。

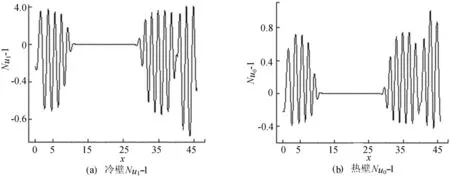
图4 冷壁、热壁的Nusselt数的变化情况

图5给出r＝1.23时，随时间推进，从腔体1／2高度处水平方向速度场、垂直方向速度场、流场、扰动浓度场在t＝806.25时的演化情况。

由图5可以看出在两边行进波控制区域和中间的传导区域可以明显区分，各个场均达到了双局部行进波的状态。

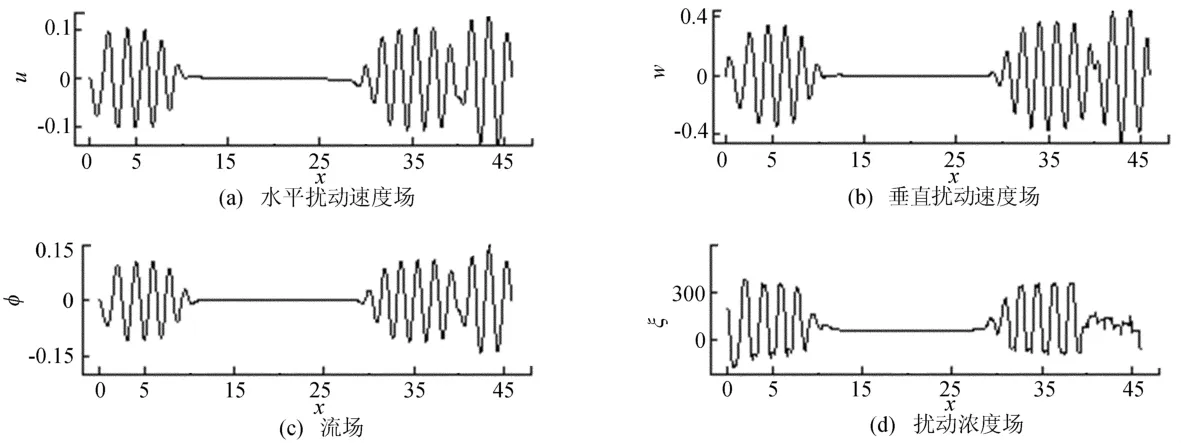
图5 r＝1.23时腔体1／2高度处达到双局部行进波时的变化

图6给出了不同Rayleigh数下，腔体1／2处 的温度场的空间变化情况。

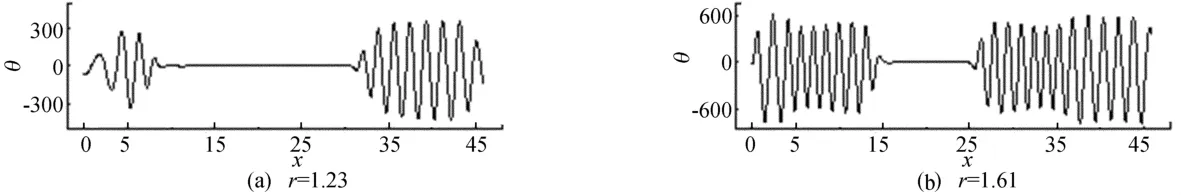
图6 不同瑞利数下腔体1／2高度处扰动温度场的空间变化

在r＝1.23时获得了稳定的局部行进波，为了探讨双局部行进波的瑞利（Rayleigh）数的依赖性，把r从1.23增加到1.61，经过长时间的计算，均得到双局部行进波，且随着Rayleigh数的增大，双局部行进波的宽度也在增加。由图6可以看出，在r＝1.23～1.61之间获得了稳定的双局部行进波。

4 结束语

本文运用高精度紧致格式求解描述混合流体对流运动的流体力学扰动方程组，并对其进行二维数值分析，讨论了长高比为46的腔体中具中等Soret效应的混合流体行进波斑图的动力学特性，在ETW波的基础上通过数值模拟得出当r＝1.23时出现了双局部行进波，并确定出其稳定性依赖瑞利数的大小，确定当r在1.23～1.61之间双局部行进波是稳定的。

［1］ Chandrasekhar S.Hydrodynamics and hydromagnetic stability［M］.New York：Dover Publication Inc，1981：1－100.

［2］ Walden R W，Kolodner P，Passner A，et al.Traveling waves and chaos in convection in binary fluid mixture［J］.Physical Review Letter，1985，55（5）：496－499.

［3］ Moses E，Fineberg J，Steinberg V.Multistability and confined traveling wave patterns in a convecting binary mixture［J］.Physical Review A，1987，35（6）：2757－2760.

［4］ Heinrichs R，Ahlers G，Cannel D S.Traveling waves and spatial variation in the convection of a binary mixture［J］. Physical Review A，1987，35（6）：2761－2764.

［5］ Harada Y，Masuno Y，Sugihara K.Traveling－wave convection in binary fluid mixtures and spatio－temporal structure［J］.Vistas in Astronomg，1993，37：107－110.

［6］ Kolodner P.Stable，unstable and defected confined states of traveling－wave convection［J］.Physical Review E，1994，50：2731－2755.

［7］ Ning L Z，Harada Y，Yahata H.Formation process of the traveling wave state with a defect in binary fluid convection［J］.Progress of Theoretical Physics，1997，98（3）：551－566.

［8］ 宁利中，齐 昕，魏炳乾，等.大长高比腔体内的混合流体行进波对流［J］.水动力学研究与进展：A辑，2006，21（4）：427－432.

［9］ 宁利中，齐 昕，余 荔，等.具有强SORET效应的混合流体Undulation行进波对流斑图［J］.力学季刊，2008，29（4）：521－529.

［10］ Ning L Z，Qi X，Yuan Z，et al.A counter propagating wave states with a periodically horizontal motion of defects［J］. Journal of Hydrodynamics，2008，20（5）：567－573.

［11］ 李国栋，田飞飞，宁利中，等.混合流体Rayleigh－Benard对流的线性稳定性分析［J］.水动力学研究与进展：A辑，2010，25（4）：446－452.

［12］ 胡 军，尹协远.双流体Poiseuille－Rayleigh－Benard流动中脉冲扰动的时空演化［J］.中国科学技术大学学报，2007，37（10）：1267－1270.

［13］ 张 华，郜余伟，武守锋.混凝土材料SHPB主动围压实验的数值模拟［J］.合肥工业大学学报：自然科学版，2012，35（2）：216－220.

［14］ 王 涛，田振夫，葛永斌.长腔体内混合流体行进波对流的高精度数值模拟［J］.水动学研究与进展：A辑，2011，26（1）：41－47.

［15］ Shu C W，Osher S.Efficient implementation of essentially nonoscillatory shock capturing schemes［J］.Journal of Computational Physics，1988，77：439－471.

［16］ Tian Z F，Li Y A.Numerical solution of the incompressible Navier－Strokes equation with a three－point fourth－order upwind compact difference schemes［C］／／Proceedings of 4th International Conference on Nonlinear Mechanics，Shanghai，China，2002：942－946.

［17］ Gupta M M.A fourth－order Poisson solver［J］.Journal of Computational Physics，1985，55（1）：166－172.

［18］ De Vahl Davis G.Natural convection of air in a square cavity：a bench mark numerical solution［J］.Int J Numer Meth Fluids，1983，3（3）：249－264.