非对称超载条件下深基坑支护结构的变形分析

吕小军， 杨 琪， 钱德玲， 刘 杰

（1.中铁上海工程局第一工程有限公司，安徽芜湖 241000；2.合肥工业大学土木与水利工程学院，安徽合肥 230009）

随着人类工程与经济活动的开展，特别是近年来大量高层、超高层建筑的兴起，一些基坑朝着超深和超大方向发展，对地上和地下空间的要求越来越高，由此而产生的大量基坑问题也越来越显著［1］。由于深基坑支护工程的复杂性和不确定性，引发的问题越来越多，甚至造成重大工程事故（如杭州地铁等）。特别是在地质条件较差的土层中，基坑的开挖、支撑和围护带来的问题常常造成附近建筑物和市政设施产生较大的变形和沉降，直接影响正常使用。因此，研究深基坑的支护问题、完善基坑设计理论，特别是研究非对称超载条件下的基坑变形，即基坑两侧地面荷载不对称的情况下产生的变形，将具有重要的现实意义。

本文根据苏州地铁1号线深基坑的围护和支撑结构的特征，采用三维有限元分析［2－3］，计算非对称超载条件下支护结构的内力和变形，并与无超载条件下的计算结果进行对比，得到了非对称超载条件下支护结构内力和变形的分布规律，研究结果将有助于提高深基坑的设计水平和安全性，并为类似工程的设计、施工和研究提供必要的数据。

1 工程概况

苏州轨道交通1号线位于苏州市市中心人民路与干将东路交会处，长约290 m，宽约22 m，为地下二层岛式，拟采用明挖法施工，地下连续墙＋内支撑围护结构体系。主体围护结构采用1 000 mm厚地下连续墙，局部采用800 mm和600 mm厚地下连续墙。A区段工程北侧邻近交通主干道和建筑物，基坑相应的超载设计值为q＝20 k N／m2，南侧比较空旷。基坑平均深度18 m，局部7.5 m，长度约为195 m，支护结构形式较为复杂，基坑中间采用对撑，角部采用角撑或斜撑，设为3道支撑，支护结构平面图如图1所示。

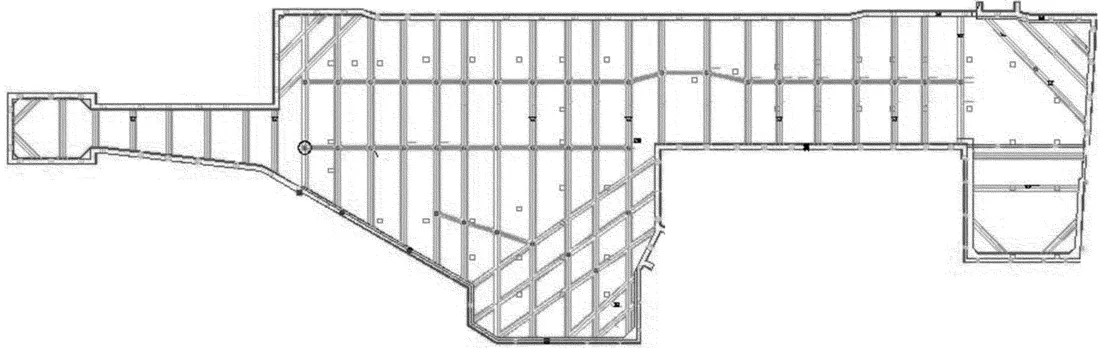
图1 支护结构平面布置图

1.1 场地工程地质条件

拟建场地地处广阔的冲积、湖积平原，为典型的水网化平原。

第1层为人工填积土，土性较杂，含碎砖、瓦片和淤泥等，工程性质较差，大部分地段厚度较大，分布于整个场区。

第2层分为上下2层。上层系晚更新世（Q3）冲湖积相沉积成因土层，为可塑和软塑黏性土，夹薄层粉土，工程性质差异较大，由于受切割，厚度变化大，局部缺失。该层内夹有浅海相、海陆交互相沉积成因的饱和砂性土和软弱黏性土，工程性质较差，总体厚度大，但各层土分布不均匀，其中，软弱黏性土厚度较大。下层为冲湖积相沉积成因的饱和砂性土，工程性质较好，较稳定地分布于整个场区，厚度较大。

第3层为中更新世（Q2）冲湖积相沉积成因土层，为硬塑－可塑－软塑黏性土，夹薄层粉土，工程性质较好，土质不均匀，总体厚度较大。

第4层为古沙洲相沉积成因的饱和砂性土层，工程性质较好，土质不均匀。

场地内埋置了各种管线，地处交通主干线和建筑物旁边，因此，基坑支护设计必须考虑基坑周边交通、建筑物及管线的安全，并严格控制基坑施工期间的地面沉降与变形。场地土层自上而下见表1所列。

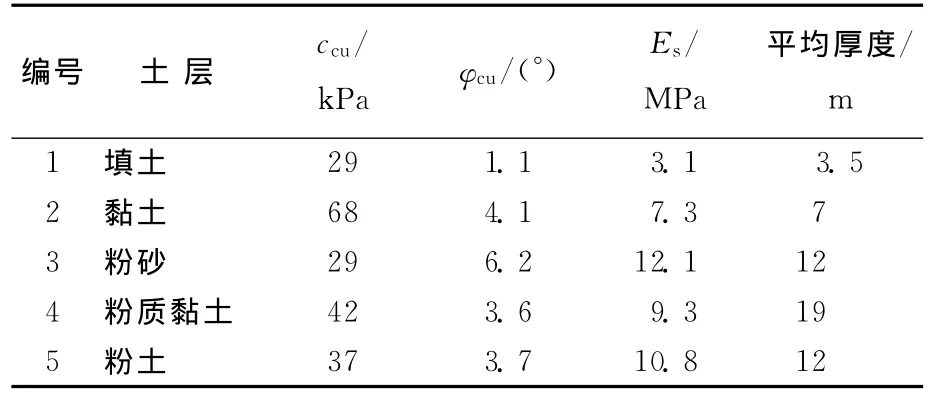
表1 苏州1号线基坑场地地质条件

1.2 监控量测

为保证基坑自身稳定和安全，以及周边道路交通、建筑物和地下管线的安全，施工过程中对基坑进行了全过程监控量测。量测的主要内容有：地表沉降及位移、建筑物及地下管线变形、水位观测、桩顶水平位移及沉降、土体水平测斜、支护桩内力、支撑轴力及立柱变形等量测。现场监控量测是监视基坑稳定、判断基坑支护设计是否合理、施工方法和工艺是否可行的重要手段，也是保证施工安全、提高经济效益的重要条件。

2 模型建立与计算

为了了解非对称超载条件下基坑支护结构的内力和变形情况，采用GTS分析软件进行计算。利用AutoCAD强大的绘图功能，将AutoCAD设计图导入GTS中进行建模，并根据实际开挖流程进行分析和计算。

针对苏州地铁A区段基坑工程的特点，考虑了初始应力，应用了“位移清零”功能，在位移清零之后再进行分步开挖和支撑的数值计算，有效地提高了模拟计算的精度。

2.1 模型的建立

根据基坑设计和施工方案，建立了三维有限元模型。由于该基坑的长度是宽度的3倍左右，考虑基坑自身的长跨效应，并结合基坑开挖过程中的步骤和时空效应，分别进行了整体分析［4－6］，计算模型如图2所示。

图2中为支护结构有限元实体模型（包括内支撑、地下连续墙和周围土体），中间线形表示钢筋混凝土内支撑、冠（腰）梁及内支撑作为梁单元来考虑［7－8］。计算域的边界为：实体模型中Z方向土体深度取基坑开挖深度的2倍，宽度自开挖边界向外取开挖深度的1倍以上。边界条件为：模型四周在X、Y方向约束，Z方向自由；模型底部在3个方向上均为约束，基坑表面自由。

图2 基坑支护结构模型图

地下连续墙平均厚度0.9 m，墙体设计高度不等，最深18 m，局部7.5 m。冠梁、腰梁、对撑和角撑的有限元模型如图2所示，混凝土强度等级为C30，相关的计算参数见表2所列。

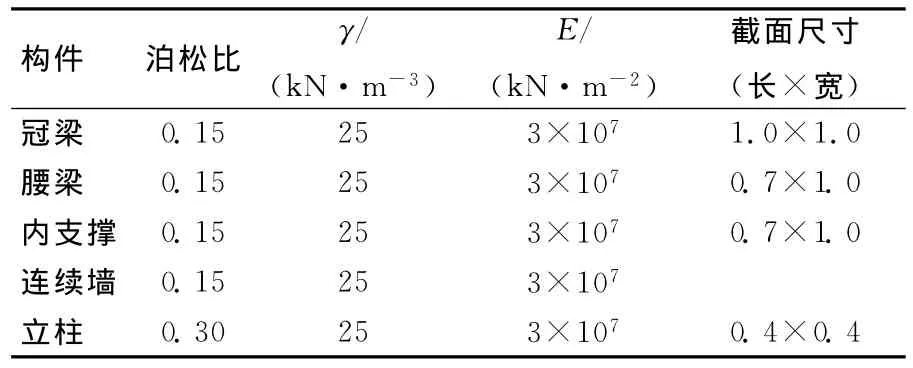
表2 支撑结构的计算参数

2.2 GTS计算结果与实测结果的对比

为保护邻近交通、建筑物和地下管线的安全，以及基坑工程本身的安全和质量，基坑开挖按规范要求，布控了大量的监测点（如图3所示）。监测数据不仅为及时调整施工和加固方案提供了依据，还为今后信息化设计和施工提供了有效的依据和参数。

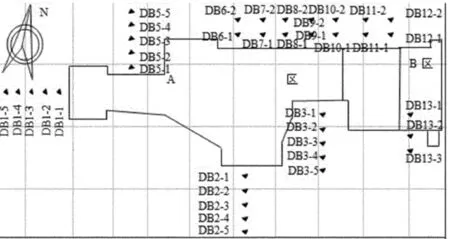
图3 监测点平面布置图

该基坑北侧紧邻交通主干线和建筑物，南侧为空地，可视为非对称超载作用下的深基坑。2008年3月完成第1层土的开挖，计算时相当于完成第1步开挖的模拟，按照施工顺序模拟至完成全部开挖和支撑。2009年11月完成底板浇注，至此，监测结果显示监测点DB3－3地表沉降值为11 mm，相同点的数值计算结果为10 mm，如图4所示，从图中看出，计算点与实测点的沉降总体趋势基本相同。

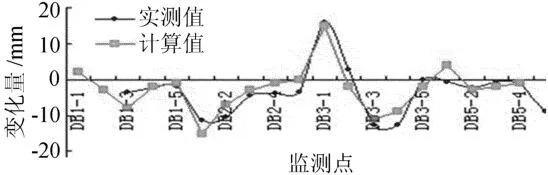
图4 实测值与计算值的对比

3 计算与分析

大多数基坑均为对称情况下的超载，为了研究非对称超载情况下的基坑变形，计算中选择2种超载状态进行分析，即相同工况条件下对称和非对称超载下地表沉降和支撑内力的差异，以此来解决实际工程中的问题和应注意的事项。

3.1 对称超载下支护结构内力和地表沉降

通过有限元分析，相同工况条件下，在开挖深度为17.3 m时（即第5道开挖），对称超载作用下的支撑轴力FX方向上的最大值为1 970 k N，主要集中在南侧第5道支撑的西南局部位置。地表沉降最大值为26.1 mm，主要集中在基坑南侧位置，北侧地表沉降17.2 mm。地下连续墙的最大负弯矩为1 390 k N·m，位于地表下11～14 m处，连续墙的位移为25.2 mm，位于墙的下部，北侧位移比南侧小，如图5和图6所示。

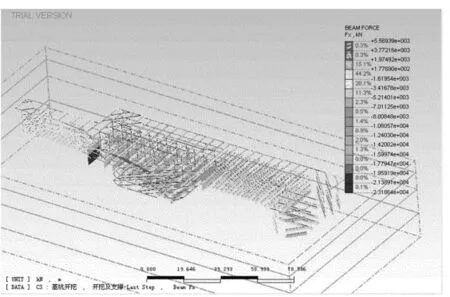
图5 对称超载下支撑轴力F X

图6 对称超载下基坑地表沉降

3.2 非对称超载下支护结构内力和地表沉降

在相同计算参数和相同工况下，开挖深度为17.3 m时，非对称超载下基坑支撑轴力和地表沉降的计算结果如图7和图8所示。在超载侧（北侧）加上10 k Pa的荷载，支撑轴力在深度13.8 m处FX方向上最大内力值为1 980 k N，地下连续墙的最大负弯矩为1 511 k N·m，出现在基坑变宽处，连续墙的位移为31.4 mm，北侧比南侧位移大。加载侧（北侧）的地表沉降为26.5 mm，比非超载侧（南侧）位移17.6 mm的地面沉降大，基坑处于应力不均衡状态。

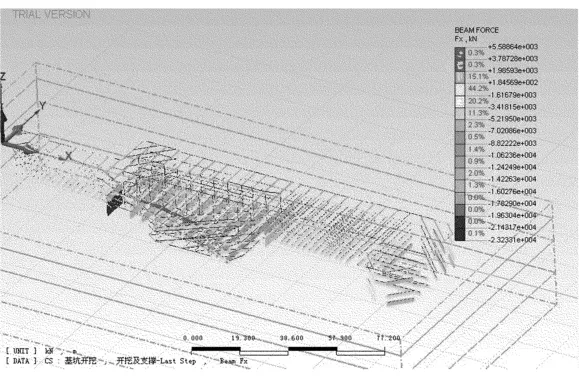
图7 非对称超载下支撑轴力F X

图8 非对称超载下基坑地表沉降

由以上结果可以得出相同开挖条件下，非对称超载条件下支撑结构内力和地表沉降的分布规律。在对称超载条件下，基坑连续墙最大水平位移为26.1 mm，两侧变形区域主要集中在地表下10.8～14.1 m处。在非对称超载作用下，超载侧连续墙的最大水平位移为31.4 mm，非超载侧连续墙最大水平位移为17.6 mm，两侧变形区域主要集中在地表下10.9～14.8 m处。这说明在非对称超载作用下，土体产生变形，超载侧土压力由静止土压力逐渐转向主动土压力，连续墙的水平位移也随着增大，同时内支撑轴力增大而产生压缩变形，并随着超载侧的变形一起向非超载侧发生偏移。文献［9］允许桩身位移为0.25%H（H为基坑深度），该基坑最大允许位移值为43.25 mm，数值计算结果为31.4 mm，满足规范要求。数值模拟结果与理论计算结果和实际情况基本吻合，对类似工程具有一定参考价值。

以上计算和分析结果表明：非对称超载状态下，基坑围护体系超载侧连续墙的内力和弯矩略大于对称超载条件下的围护结构，但超载侧的位移却较大。也就是说，在非对称超载条件的情况下，基坑的位移较大，其稳定性处于最不稳定的状态。而在常规设计时，通常是考虑对称超载条件，往往忽略非对称超载的情况。因此，在设计和施工中，应重视非对称超载条件下，超载侧基坑的变形［10］。

4 结束语

通过有限元计算和分析，得到了非超载条件下基坑支护结构内力与水平位移的分布规律。实际工程中常常将基坑两侧看作对称超载，而忽略了非对称超载作用下基坑存在的不安全因素。根据我国设计规范GB 50009－2001［11］，设计过程分为承载力极限状态和正常使用极限状态，非对称超载作用下的基坑相对于两侧均有超载作用的基坑，在墙身水平力及墙身弯矩上相差不大，设计时能够满足承载力极限状态下的强度要求。但是，此时墙身水平位移的显著增大却经常不能满足正常使用极限状态下的相关要求，为后续施工过程留下了安全隐患。在设计时应对非对称超载作用的基坑进行定量分析，验算围护结构的水平位移，使之控制在合理的范围之内。同时，在施工过程中应监测围护结构的水平位移，通过监测数据及时掌握围护结构体系的动态，必要时应采取有效的施工措施减少围护结构的水平位移。类似于本基坑非对称超载情况的现象十分普遍，为了保证工程质量以及人民生命财产的安全，对非对称超载作用下的基坑，在设计和施工中应注重超载侧围护结构的变形。

［1］ 唐孟雄，陈如桂，陈 伟.深基坑工程变形控制［M］.北京：中国建材工业出版社，2006：5－67.

［2］ 赵海燕，黄金枝.深基坑支护结构变形的三维有限元分析与模拟［J］.上海交通大学学报，2001，35（4）：610－613.

［3］ 陆新征，宋二祥.某特深基坑考虑支护结构与土体共同作用的三维有限元分析［J］.岩土工程学报，2003，25（4）：488－491.

［4］ 宋二祥，娄 鹏.某特深基坑支护的非线性三维有限元分析［J］.岩土力学，2004，25（4）：538－543.

［5］ 俞 晓.深基坑开挖与支护的模型试验与ANSYS分析研究［D］.武汉：武汉理工大学，2005.

［6］ 芮 瑞，夏元友.基于三维有限元的地下连续墙深基坑逆作法施工方案设计［J］.岩土力学，2008，29（5）：1391－1395.

［7］ Ou Changyu，Chiou D C，Wu T S.Three－dimensional finite element analysis of deep excavations［J］.Journal of Geotechnical Engineering，1996，122（5）：337－345.

［8］ 秦四清.深基坑工程优化设计［M］.北京：地震出版社，1998：14－24.

［9］ JGJ 120－99，建筑基坑支护技术规程［S］.

［10］ 王 凯，钱德玲.液化场地的桩－土－上部结构振动台模型试验的研究［J］.合肥工业大学学报：自然科学版，2011，34（11）：1687－1691.

［11］ GB 50009－2001，建筑结构荷载规范［S］.