Simpson牛顿公式的一种改进

李洋洋， 郭清伟

（合肥工业大学数学学院，安徽合肥 230009）

0 引 言

迭代法是求解非线性方程的最为常用的方法之一，主要有简单迭代法、弦截法、抛物线法、牛顿法及其各种变形的迭代方法。文献［1］提出Simpson牛顿方法和几何平均方法，且证明其三阶收敛到单根；文献［2］利用反函数的求导法则，提出了Homeier－Simpson牛顿方法，且证明其三阶收敛到单根；文献［3－4］讲述了关于非线性方程求根的一些基础知识；文献［5］中介绍了一类具有五阶收敛的牛顿方法；文献［6－7］提出调和平均牛顿方法和中点牛顿方法及改进牛顿法，且证明其三阶收敛到单根；文献［8］介绍了一类四阶牛顿变形方法；文献［9］讨论了平方收敛公式的一个5阶加速方法；文献［10］介绍了科茨求积公式与牛顿公理相结合得出的各种迭代格式，至少三阶收敛到单根。在已有的迭代法中，有的收敛阶虽高但计算效率低下，有的2个方面都不理想。考虑到收敛阶和计算效能问题，本文基于文献［1，2，5］和文献［10－12］，提出了一种新的迭代格式，称为改进的Simpson牛顿方法，简记为XSN方法；证明了该方法对单根而言具有三阶收敛性，对非单根而言具有线性收敛性，与同类方法相比，在计算效率方面有了一定的改善。

1 预备知识

为研究迭代序列的收敛速度和收敛效率，先给出效率指数的定义、收敛阶定义及收敛定理。

定义1 设迭代序列｛xn｝∞0的收敛阶为p≥1，每步迭代的计算量为ω，则称e为迭代序列的效率指数［1］，即

定义2 设迭代过程xn＋1＝φ（xn）收敛于方程x＝φ（x）的根x＊，如果迭代误差en＝xn－x＊，当n→∞时，成立下列渐进关系式：

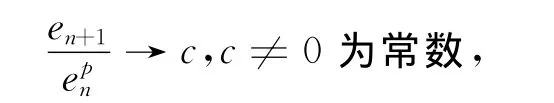
则称该迭代过程是p阶收敛的［2］。

定理1 对于迭代过程xn＋1＝φ（xn），如果φ（p）（x）在所求根x＊的邻近连续，并且有：

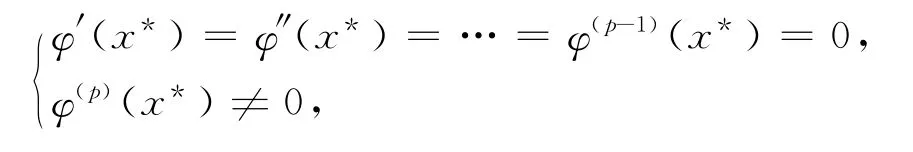
则该迭代过程在点x＊邻近是p阶收敛的［3］。

2 新算法的推导

设α是方程f（x）＝0的根，f（x）是可导函数，由牛顿公理显然成立：

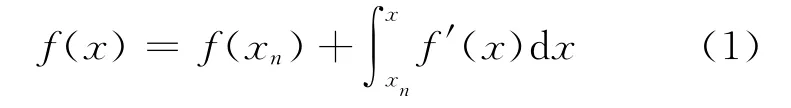
将（1）式中右端积分用数值积分Simpson公式近似代替，并令x＝α，则

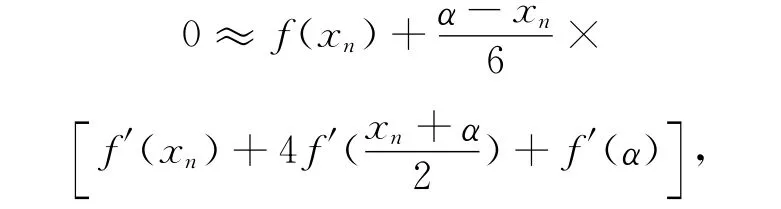
其中，用xn＋1近似代替α，整理得到迭代格式：

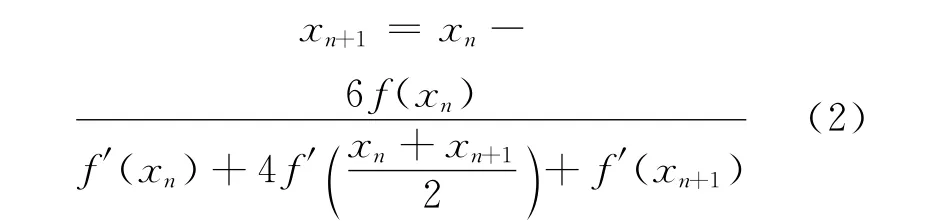
（2）式中关于xn＋1是隐式的，给求解带来很多麻烦，为避免隐式求解，提出组合格式，即

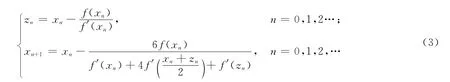
（3）式是经典牛顿方法与Simpson公式结合得到的，这就是文献［1］所给出的迭代方法，称为Simpson牛顿方法，简记为SN方法。

衡量一个迭代法的优劣除了考察其收敛阶外，还要考虑算法的效率指数。从（3）式可以明显看出，迭代一次需要计算1次函数值和3次导数值，考虑到迭代的计算效率，如果收敛阶不变，能减少函数值或导数值的计算次数，提高计算的效能。由此将和在xn泰勒展开，可得：

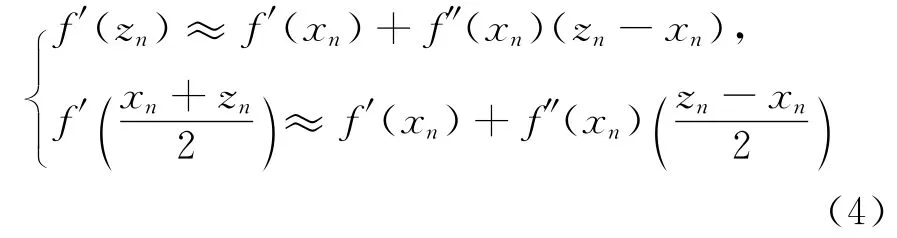
将（4）式代入（3）式，得到本文的迭代公式：

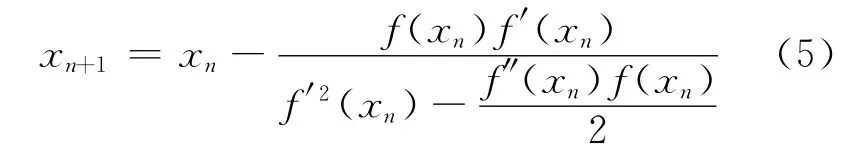
其中，n＝0，1，2，…。

显然，（5）式迭代一次需要计算1次函数值和2次导数值。如果将函数与其各阶导数的计算量看作相同，每迭代一次，（5）式就比（3）式减少1次计算量，然而它们的收敛阶相同，根据定义1可知（5）式的计算效率要高于（3）式。为了方便，把本文的迭代公式（5）式简记为XSN方法。

3 收敛性分析及计算效能比较

3.1 定理2及其证明

定理2 若方程f（x）＝0在某一区间存在实根x＊，且f″（x）在x＊某一邻域内连续，则有：

（1）当x＊是f（x）＝0的单根时，XSN方法是三阶收敛的。

（2）当x＊是f（x）＝0的m（m≥2）重根时，XSN方法是线性收敛的。

下面证明当f′（x＊）和f″（x＊）均不为零时，迭代格式三阶收敛于f（x）＝0的根x＊。

证明 （1）由（5）式知XSN方法的迭代函数为：

计算φ（x）在方程的根x＊处的各阶导数值：

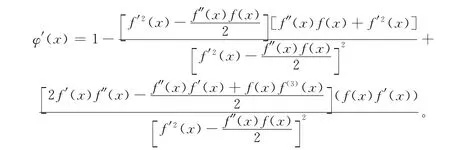
而f（x＊）＝0，代入整理得φ′（x＊）＝。当f（x＊）＝0时，有

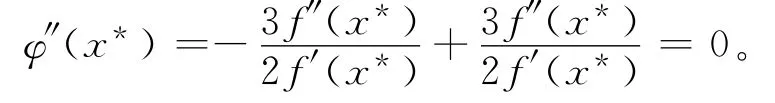
而

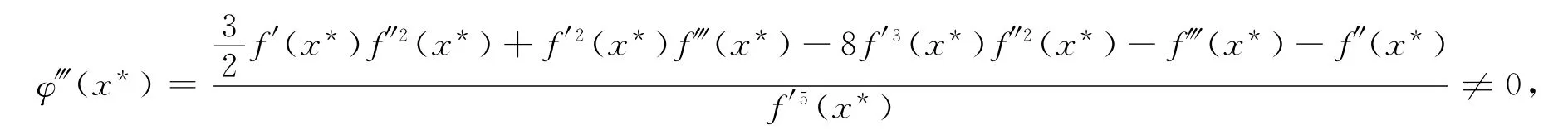
根据定理1可得XSN方法是三阶收敛，其收敛阶高于牛顿迭代法。

（2）设x＊是f（x）＝0的m（m≥2）重根，则

f（x＊）＝0， f′（x＊）＝0，…，f（m－1）（x＊）＝0， f（m）（x＊）≠0。

从而由泰勒展开公式得：

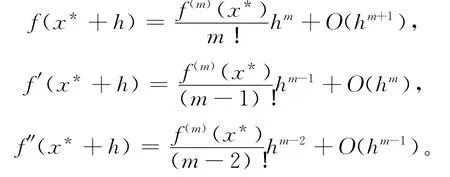
代入迭代函数中，整理得：

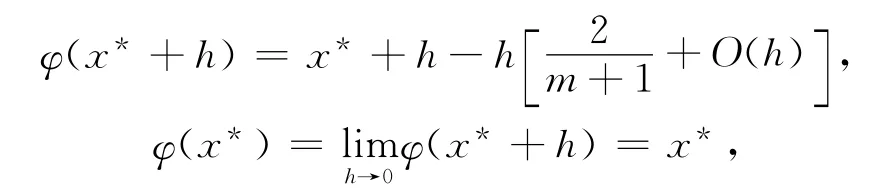
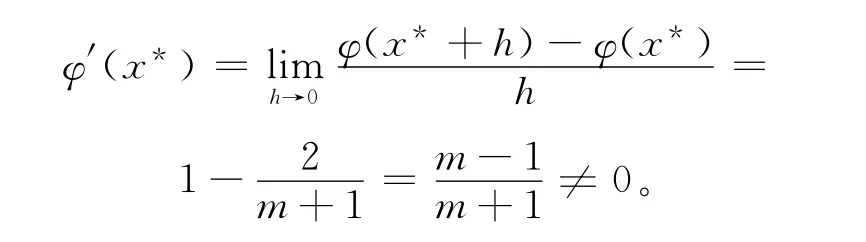
故由定理1得XSN方法在重根附近是线性收敛的，从而定理2证毕。

当方程根的重数m已知时，改进的XSN方法如下：

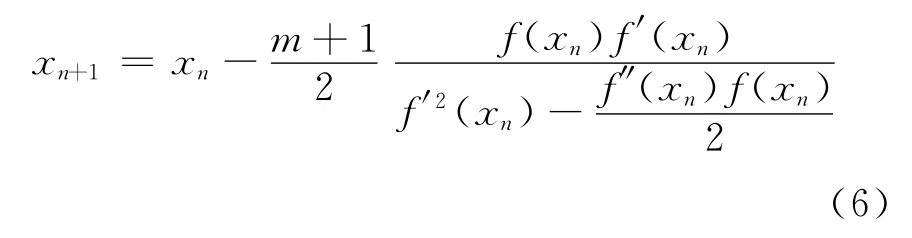
其迭代公式如下：

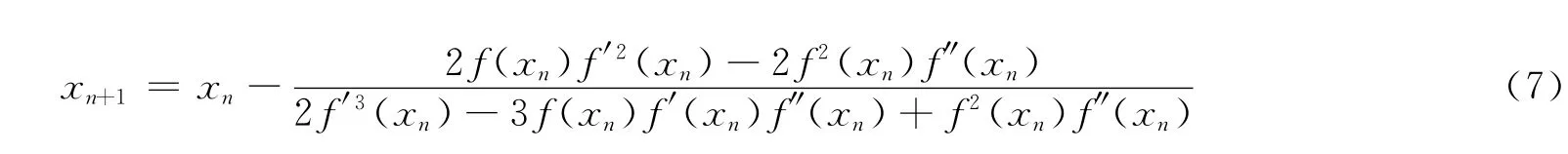
推论1 当x＊是f（x）＝0的m（m≥2）重根时，当重数m已知时，改进的XSN方法（6）式是平方收敛的；当重数m未知时，改进的XSN方法（7）式是三阶收敛的。

由定理2的证明过程即可得到该推论。

3.2 定理3及其证明

定理3 XSN方法的效率指数高于文献［1］的SN方法、文献［5］的五阶牛顿方法及文献［8］的四阶牛顿方法。

证明 （1）XSN的收敛阶为3，每次迭代的计算量为3n，所以效率指数为：

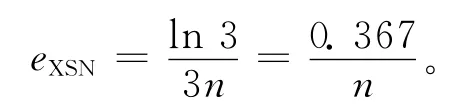
（2）文献［1］中SN方法的收敛阶为3，每次迭代的计算量为4n，所以效率指数为：

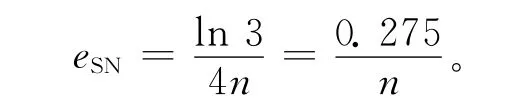
（3）文献［5］中的迭代方法收敛阶为5，每次迭代的计算量为5n，所以效率指数为：

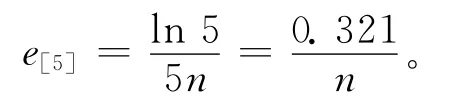
（4）文献［8］中的迭代方法收敛阶为4，每次迭代的计算量为4n，所以效率指数为：

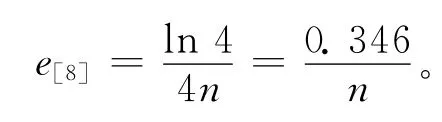
则有eSN＜e［5］＜e［8］＜eXSN，至此，定理3得证。

定理3也表明，虽然有些迭代方法收敛阶提高了，但并没有真正提高计算的效能。

4 数值试验比较

（1）算例1。求方程f（x）＝sin2（x）－x2＋1的根，取初值x＝1.5。

反复使用本文方法（XSN法）与正割法迭代，令｜xn＋1－xn｜≤10－5时终止迭代，得到xn序列，见表1所列。

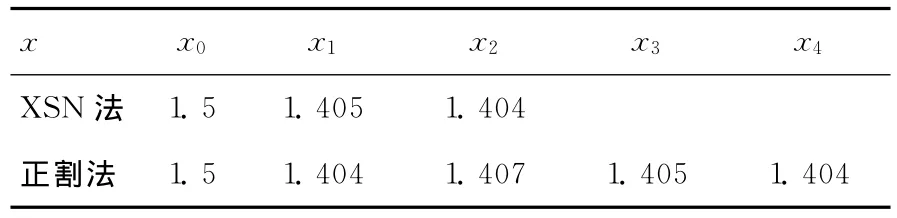
表1 使用XSN法与正割法迭代得到的xn序列

（2）算例2。求方程f（x）＝x3－x－1的根，取初值x0＝0。

反复使用本文方法（XSN法）与经典牛顿法，令｜xn＋1－xn｜≤10－5时终止迭代，得到xn序列，见表2所列。

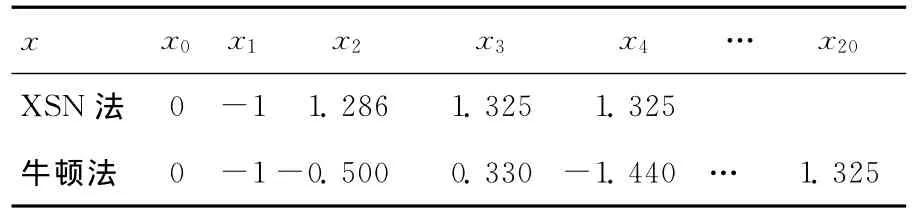
表2 使用XSN法与经典牛顿法迭代得到的x n序列

明显地，牛顿法用20次才达到精度，而XSN方法只4次就达到了很好的收敛效果。

（3）算例3。求方程f（x）＝x3＋4x2－10的根，取初值x0＝1。

反复使用本文方法（XSN法）与经典牛顿－Cauchy法，令｜xn＋1－xn｜≤10－5时终止迭代，得到xn序列，见表3所列。

表3 使用XSN法与经典牛顿－Cauchy法迭代得到的x n序列

通过表1～表3的迭代结果可以看出，XSN方法具有较快的收敛速度和较高的数值精度。

5 结束语

目前有很多迭代公式，但主要都是对经典牛顿法的各种变形，虽然收敛阶有所提高，但是计算效能并没有真正提高。本文基于收敛阶和计算效率2个方面考虑，对Simpson－牛顿法进行改进，数值验证非常有效，所以该方法在非线性方程求根中具有很高的实用价值。

［1］ 王 霞，赵玲玲，李飞敏.牛顿方法的两个新格式［J］.数学的实践与认识，2007，37（1）：72－76.

［2］ 王 霞，张银银.一个三阶牛顿变形方法［J］.数学的实践与认识，2009，39（14）：14－18.

［3］ 马振华.现代应用数学手册：计算与数值分析卷［M］.北京：清华大学出版社，2005：163－176.

［4］ Cautschi W.Numerical analysis：an introduction［M］.Boston：Birkhauser，1997：50－100.

［5］ 苏岐芳，李希文.一类具有五阶收敛的牛顿改进法［J］.台州学院学报，2008，30（6）：1－4.

［6］ Ozban A Y.Some variants of Newton’s methods［J］.Applied Mathematics Letters，2004，17（9）：677－682.

［7］ 朱 琳.关于牛顿迭代公式的改进［J］.宁夏师范学院学报：自然科学版，2011，32（3）：88－89.

［8］ 赵玲玲，王 霞.一类四阶牛顿变形方法［J］.数学的实践与认识，2008，38（9）：102－106.

［9］ 林开勇，陶芳宽，江 平，等.平方收敛公式的一个5阶加速方法［J］.合肥工业大学学报：自然科学版，2009，32（11）：1763－1765.

［10］ 薛雅萍，吴开谡，刘晓晶.基于等距节点积分公式的牛顿迭代法及其收敛阶［J］.数学的实践与认识，2007，37（24）：34－38.

［11］ 刘雅妹，王 霞.一类新的求解非线性方程的七阶方法［J］.数学的实践与认识，2011，41（14）：239－245.

［12］ Chun C B.Some fourth－order iterative methods for solving nonlinear equations［J］.Appl Math Comput，2008，195：454－459.