具有公共边的双圈图的奇优美标号及其算法

刘家保， 王 林， 陆一南

（安徽新华学院公共课教学部，安徽合肥 230088）

0 引 言

关于图的优美性，文献［1］提出“所有的树都是优美的”著名优美树猜想，奇优美标号是一类特殊的优美标号，具有奇优美标号的图类是奇优美图。文献［2］给出了优美图的定义。到目前为止，国内外已取得很多关于优美图的研究成果［1－9］。本文研究一类具有公共边的双圈图奇优美标号。

1 基本概念

定义1 对于一个简单图G＝（V，E）有a个顶点和b条边，存在函数L：V（G）→｛0，1，2，…，2b－1｝是单射的，诱导出函数L′：E（G）→｛1，3，…，2b－1｝，且L′（e＝uv）＝｜L（u）－L（v）｜是双射的，称图G具有奇优美标号，且称图G为奇优美图［1］。

定义2 2个圈图Cn共享一条公共边的图类，记为双圈图D（n），设Cn∩Cn＝e＝uv，u，v∈V（D（n）），e＝uv∈E（D（n）），双圈图D（n）满足以下条件：

（2）顶点集V（D（n））＝｛vi｜1≤i≤n｝，顶点数｜V（D（n））｜＝2n－2。

（3）边集E（D（n））＝｛vivi＋1｜1≤i≤2n－3｝∪｛v2n－2v1｝∪｛v（n＋2）／2v3n／2｝，边数｜E（D（n））｜＝2n－1。

2 主要结果

定理1 对∀n∈N＊，n≡0（mod 4）或者n≡2（mod 4），双圈图D（n）是奇优美图。

证明 双圈图D（n）顶点数为｜V（D（n））｜＝2n－2，边数为｜E（D（n））｜＝2n－1，2个单圈图公共的一条边为e＝v（n＋2）／2v3n／2。定义函数L： V（D（n））→｛0，1，2，…，2｜E（D（n））｜－1｝＝｛0，1，2，…，4n－3｝，边标号定义为L′（piqj）＝｜L（pi）－L（qj）｜，其中pq∈E（D（n）），给出图D（n）各顶点的标号算法。

2.1 情形1（n≡0（mod 4））

（1）当1≤i≤n＋1时，有

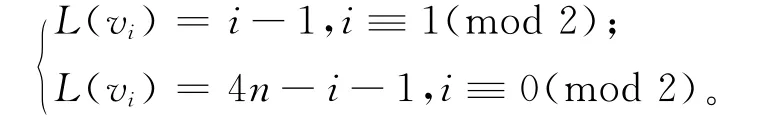
（2）当n＋2≤i≤3n／2时，有

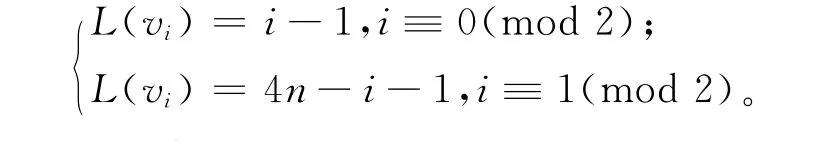
首先证明L是从顶点集V（D（n））到｛0，1，2，…，4n－3｝的单射函数。

令A＝｛L（vi）｜1≤i≤2n－2｝，则

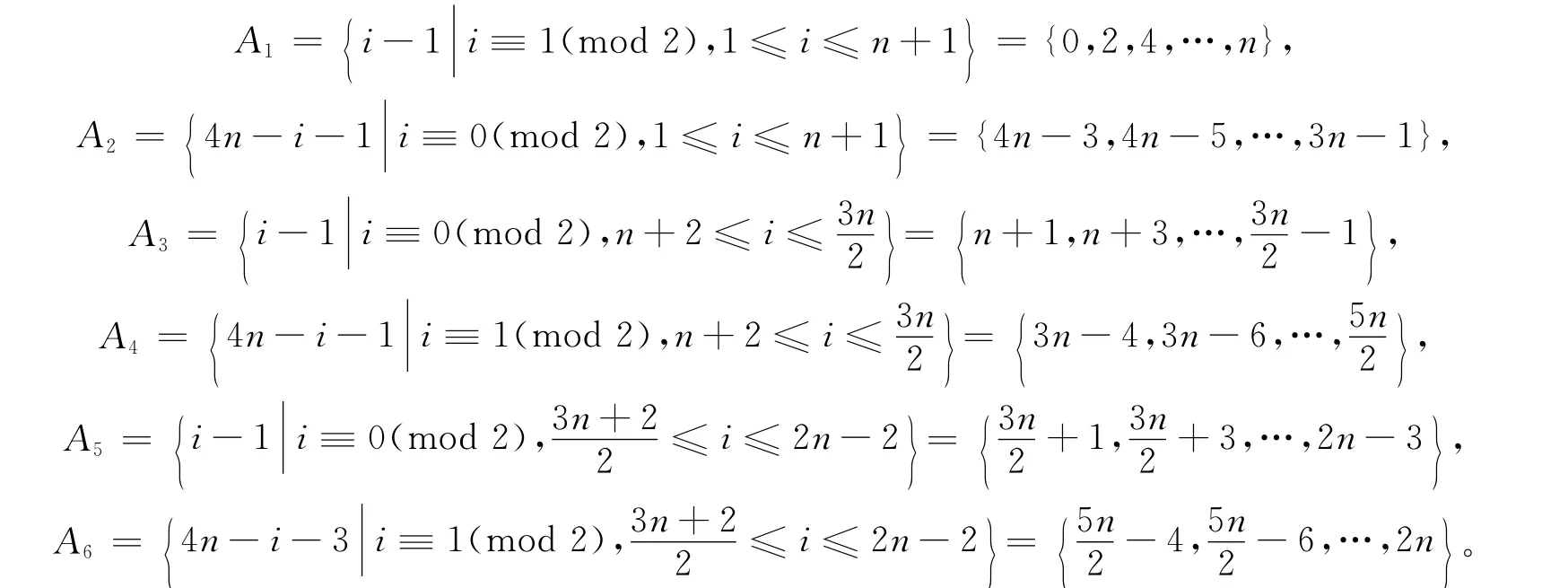
因此，A＝A1∪A2∪A3∪A4∪A5∪A6是所有顶点标号的集合，且有：

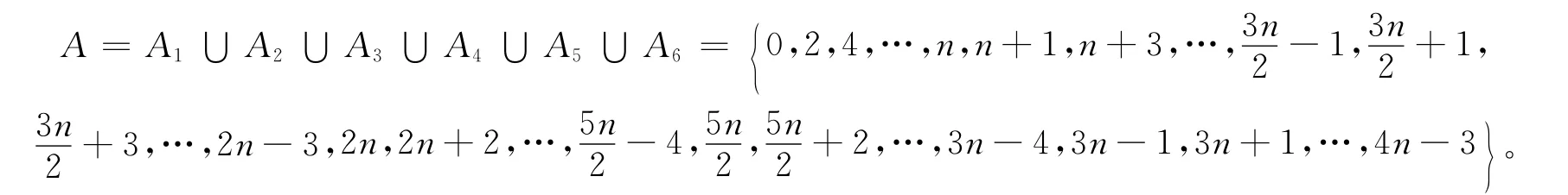
由上可知，A⊆｛0，1，2，…，4n－3｝，所有顶点的标号是各不相同的，所以L是一个从V（D（n））到｛0，1，2，…，4n－3｝的单射函数。

其次，证明L′是从E（D（n））到｛1，3，…，4n－ 3｝的双射函数。

令B＝｛L′（vivi＋1）｜1≤i≤2n－3｝∪｛L′（v（n＋2）／2v3n／2）｝∪｛L′（v2n－2v1）｝，则有：

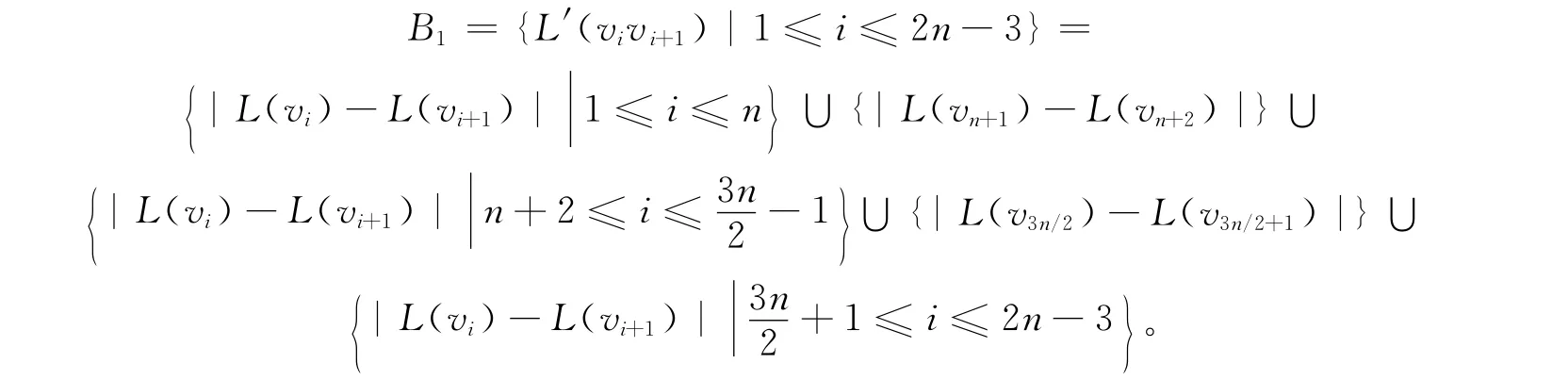
因为

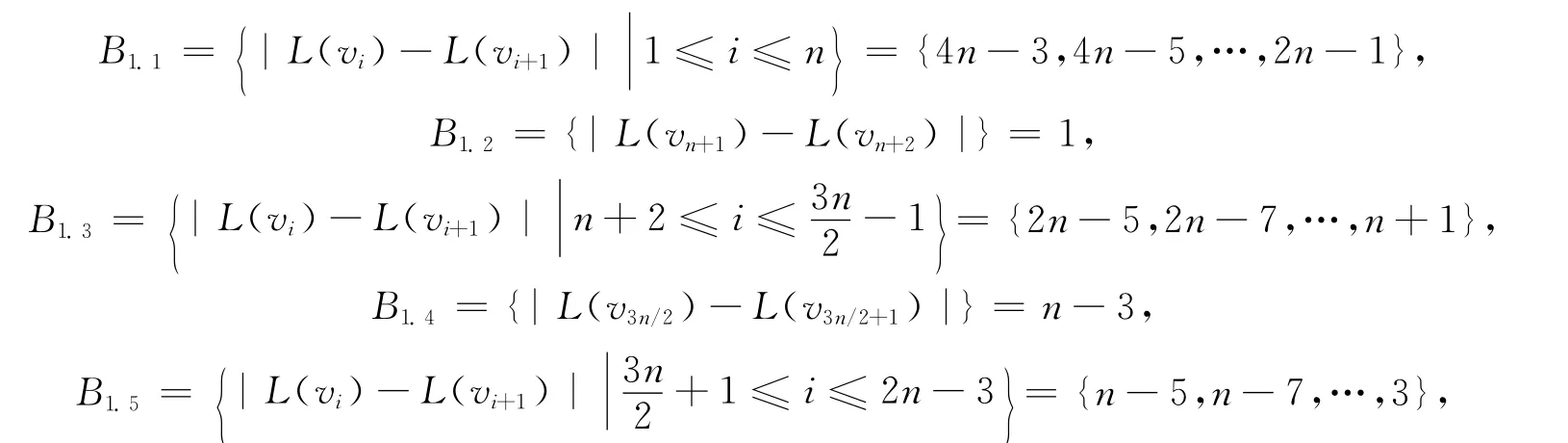
所以

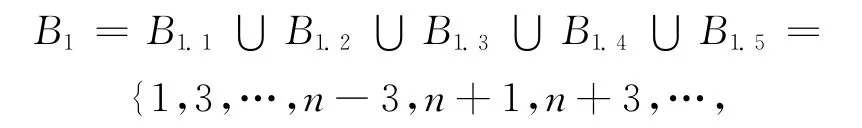
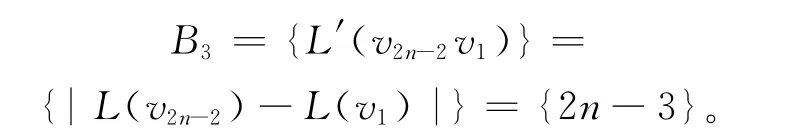
因此，B＝B1∪B2∪B3是所有边的标号的集合，且有：

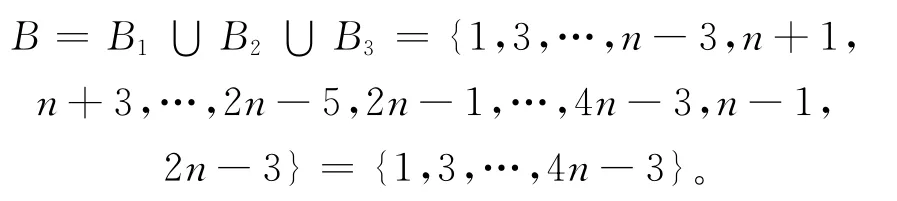
由上述可知，每条边的标号是各不相同的，且边的标号的集合为｛1，3，…，4n－3｝，所以L′是一个从E（D（n））到｛1，3，…，4n－3｝的双射函数。

根据奇优美标号的定义，对∀n∈N＊，且图D（n）的n确定，双圈图在n≡0（mod 4）的情形下是奇优美图。

2.2 情形2（n≡2（mod 4））

（1）当1≤i≤n＋1时，有

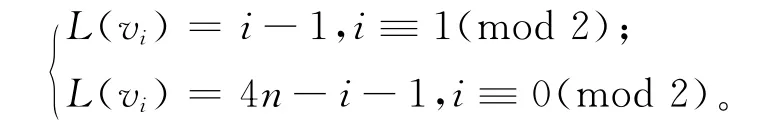
（2）当n＋2≤i≤3n／2时，有

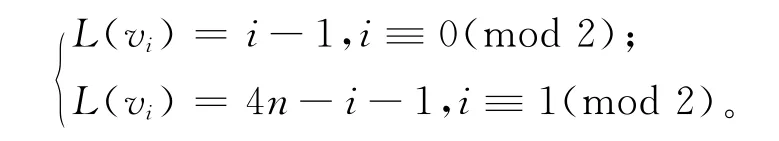
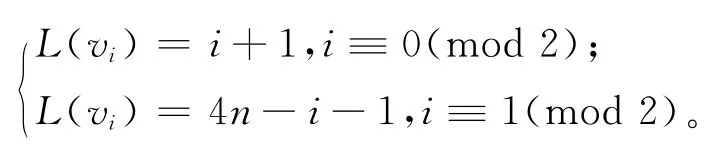
下面证明L是从顶点集V（D（n））到｛0，1，2，…，4n－3｝的单射函数。

令C＝｛L（vi）｜1≤i≤2n－2｝，则所有顶点标号的集合C⊆｛0，1，2，…，4n－3｝，所有顶点的标号是各不相同的，所以L是一个从V（D（n））到｛0，1，2，…，4n－3｝的单射函数。

同理证明L′是从E（D（n））到｛1，3，…，4n－3｝的双射函数。

令D＝｛L（vivi＋1）｜1≤i≤2n－3｝∪｛L（v（n＋2）／2v3n／2）｝∪｛L（v2n－2v1）｝，有

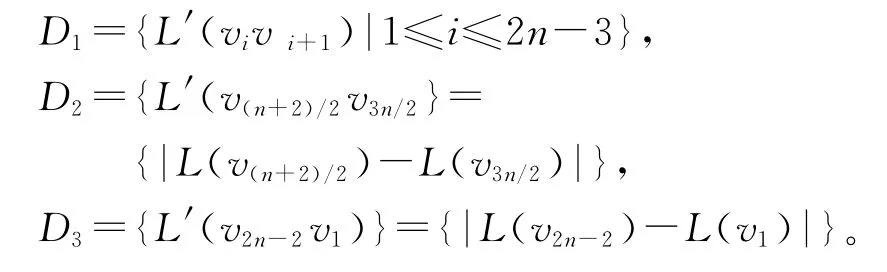
由上述可知，所有边的标号的集合D＝D1∪D2∪D3＝｛1，3，…，4n－3｝，每条边的标号是各不相同的，所以L′是一个从E（D（n））到｛1，3，…，4n－3｝的双射函数。

根据奇优美标号的定义，对∀n∈N＊，且图D（n）的n确定，双圈图D（n）在n≡2（mod 4）的情形下是奇优美图。

综上所述，定理1得证。

3 结束语

本文探索了一类具有公共边的双圈图D（n）的奇优美标号，运用算法设计与分析的理论思想设计了求解本类双圈图顶点和边标号的算法，并获得了任意顶点数双圈图的奇优美标号，最后对双圈图D（n）是否为奇优美图进行了严格论证。

［1］ Rosa A.On certain valuations of the vertices of a graph［C］／／Theory of Graphs（Int Symposium，Rome，July 1966），Gordon and Breach，N Y and Dunod Paris，1967：349－355.

［2］ Golomb S W.How to number a graph：graph theory and computing［M］.New York：Academic Press，1972：23－27.

［3］ 刘家保，潘向峰.轮形图和扇形图的优美性［J］.安徽大学学报：自然科学版，2009，133（4）：11－13.

［4］ 严谦泰.积图Pn×Pm的奇优美性和奇强协调性［J］.系统科学与数学，2010，30（3）：341－348.

［5］ 刘家保，张 季，聂东明.一类新的联图的优美标号算法［J］.汕头大学学报：自然科学版，2011，26（1）：8－10.

［6］ 郭文富.关于图B（m，n，p）的优美性［J］.数学杂志，1995，15（3）：345－351.

［7］ 严谦泰.关于P2r，2mP2r，2m的优美标号［J］.系统科学与数学，2006，26（5）：513－517.

［8］ 刘家保，王 林.一类优美图的计算机算法［J］.汕头大学学报：自然科学版，2011，26（2）：23－28.

［9］ 刘家保，王 林，陆一南.双圈图G（n，m）的奇优美标号及其算法［J］.合肥工业大学学报：自然科学版，2012，35（5）：708－710.