威布尔分布族参数的经验Bayes检验

黄金超， 凌能祥

（1.合肥工业大学数学学院，安徽合肥 230009；2.滁州职业技术学院基础部，安徽滁州 239000）

0 引 言

经验Bayes检验函数问题在文献中已有许多研究，对于连续型单参数指数族参数的EB检验问题，文献［1－4］对其做了不同程度的研究，文献［5］研究了刻度指数族参数的经验Bayes单侧检验问题，但以上文献都是对指数族中的x 1次幂条件下讨论参数的检验问题，本文在“线性损失”下，研究威布尔（Weibull）分布族刻度参数的经验Bayes检验问题，把含有刻度参数指数族中的x次幂推广到任意的m次方（m＞0）。

设随机变量X条件概率密度［6］为：

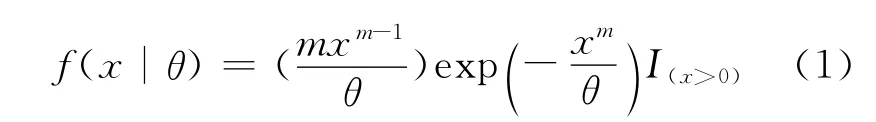
其中，m和θ分别为形状参数和刻度参数（m＞0），且本文假定m为已知常数，样本空间为χ＝｛x｜x＞0｝，参数空间为Ω＝｛θ｜θ＞0｝。Weibull分布是威布尔于1939年首次引入的，若形状参数m＝1，便得到通常的指数分布族。它在可靠性理论中有广泛的应用，如可以用来描绘疲劳失效、真空失效和轴承失效等寿命分布；它还运用于由某一局部失效引起全部失效的现象［7］；同时在工程实践、生存现象及气象预测等领域也有广泛的应用。另外，有关该分布刻度参数的EB检验的相关报道并不多，因此研究威布尔分布族刻度参数经验Bayes检验是非常有意义的。

设参数θ的先验分布为G（θ），本文考虑分布族（1）式中参数θ的EB单侧检验问题为：

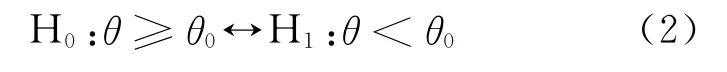
其中，θ0＞0为已知常数。

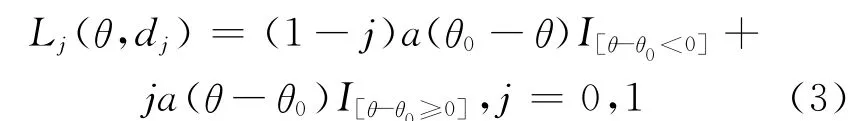
其中，a为正常数；D＝｛d0，d1｝为行动空间，d0表示接受H0，d1表示否定H0；I［A］为集合A的示性函数。设

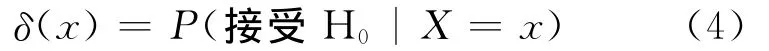
为随机化判别函数，则在先验分布G（θ）下δ（x）的风险函数为：

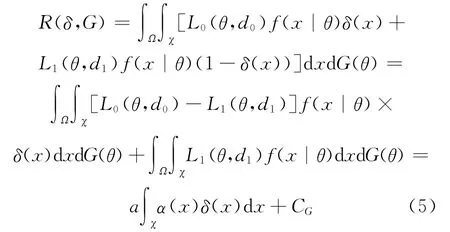
其中，CG＝∫ΩL1（θ，d1）d G（θ）；

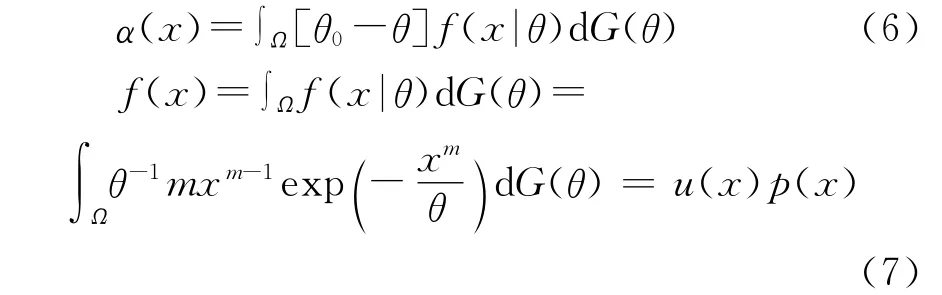
f（x）为r.v.X的边缘分布，而u（x）＝mxm－1，

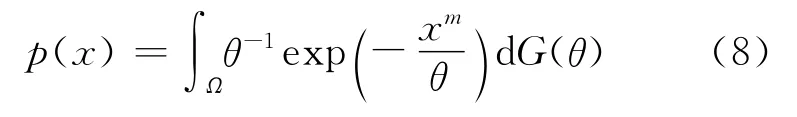
由于

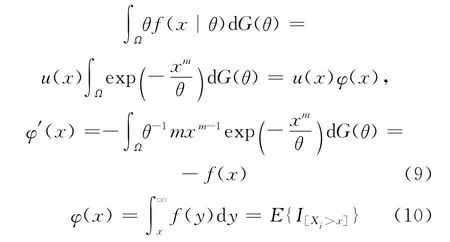
故由（6）式可知：

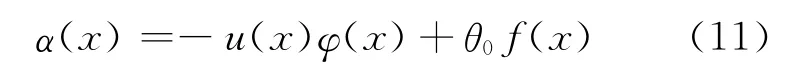
由（5）式和（6）式易见Bayes判决函数为：

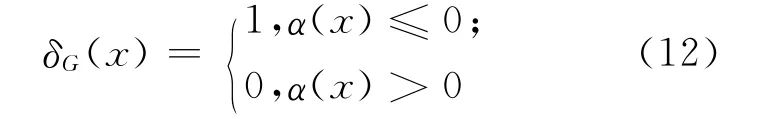
其Bayes风险为：

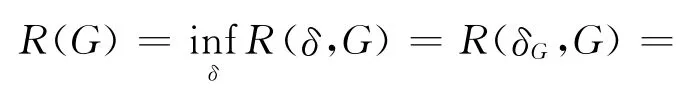
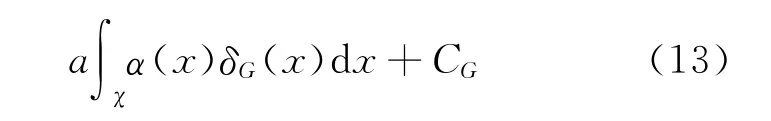
上述风险当先验分布G（θ）已知，且δ（x）＝δG（x）是可以达到的，但此处G（θ）未知，因而δG（x）无使用价值，于是考虑引入EB方法。

1 EB检验函数的构造

设X1，X2，…，Xn和X是独立同分布（iid）样本，它们具有共同的边缘密度函数，如（7）式，通常称X1，X2，…，Xn为历史样本，称X为当前样本，令f（x）为X1的概率密度函数，本文假定Cs，α为R1中一族概率密度函数，其s阶导数存在，连续且绝对值不超过α，s＞1为正整数，首先要构造α（x）的估计量。

令Kr（x）（r＝0，1，…，s－1）是Borel可测的有界函数，在区间（0，1）之外为0，且满足条件：

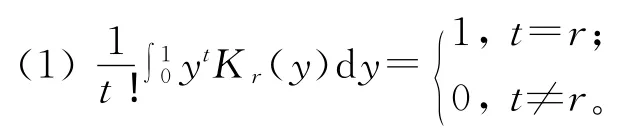
其中，t＝1，2，…，s－1。

（2）Kr（x）在R1上除有限点集E0外是可微的，且

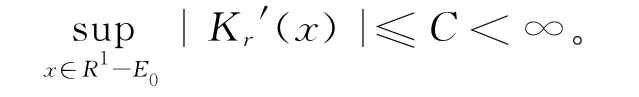
记f（0）（x）＝f（x），f（r）（x）表示对f（x）的第r阶导数，r＝0，1，…，s。由文献［8－10］定义密度函数f（x）的核估计为：

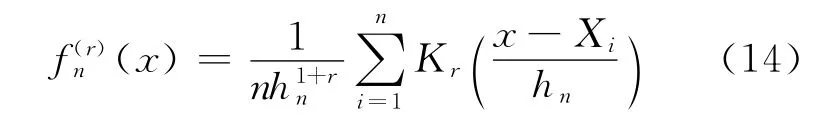
其中，｛hn｝为正数序列，且＝0；Kr（x）为满足条件（1）、条件（2）的核函数。由于

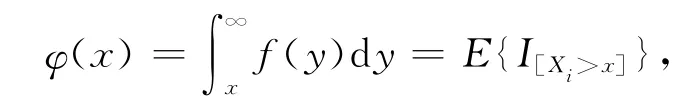
因此φ（x）的估计量定义为：

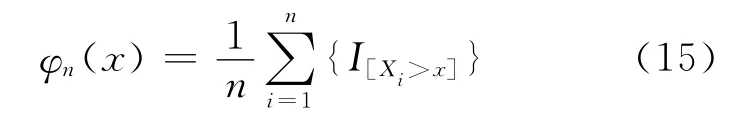
所以α（x）的估计量为：

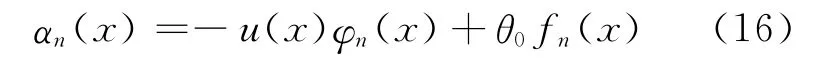
其中，fn（x）由（14）式给出。所以EB检验函数定义为：

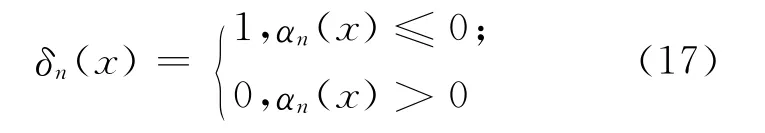
令En表示对r.v.X1，X2，…，Xn的联合分布求均值，则δn（x）的全面Bayes风险为：

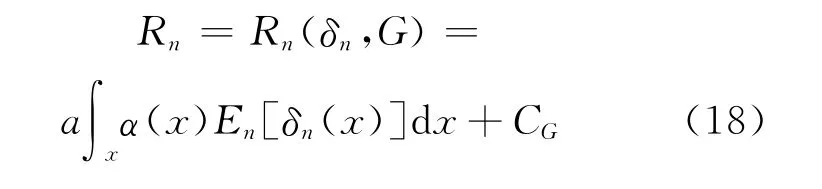
令c，c0，c1，c2…为常数，即使在同一式中它们也可能有不同的数值。

引理1 设f（r）n（x）由（14）式定义，其中X1，X2，…，Xn为独立同分布样本序列，若条件（1）、条件（2）成立，且f（x）连续，对∀x∈χ，则有：

（1）若f（r）（x）关于x连续，则当且时，有。

（2）若f（x）∈Cs，α，当取时，对0＜λ≤1，有。

证明 先证结论（1）。由Cr不等式可知：

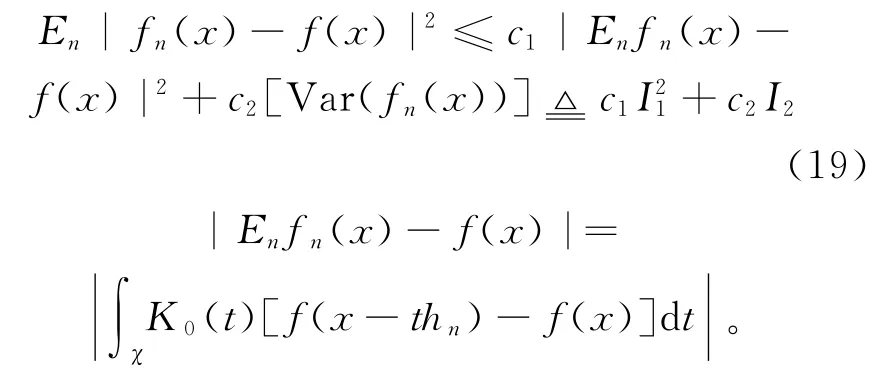
因为f（x）∈Cs，α，由Taylor展开得：

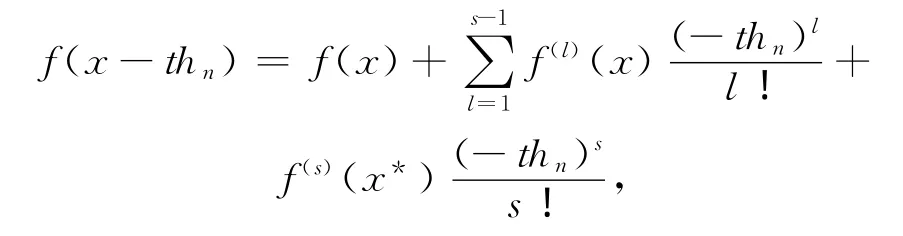
其中，x－thn≤x＊≤x。由核函数的性质可知：

玉树地处青藏高原腹地，抗震救灾任务异常艰巨。高原缺氧，低温高寒，路阻电断，余震不断。艰难险阻面前，我们看到的是水利人更加迅捷、更加统一、更加有序、更加科学、更加有力、更加有效的抗震救灾行动：迅速反应，统一指挥，科学研判，艰苦努力，成效显著。目前，震区水利工程设施震损情况初步摸清，震损供水、供电设施快速修复，应急排险和防范次生灾害工作抓紧进行，水利灾后重建规划编制工作全面启动，各项协调保障工作有序开展。4月19日，震区第一项水利灾后重建工程——禅古水电站水库大坝除险开工。水利人以最快的速度，用最短的时间，让灾区群众重新用上了电，喝上了干净的水。

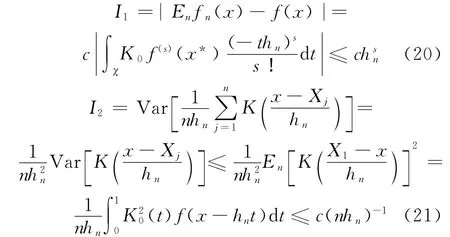
下面证明结论（2）。由Cr不等式可知：

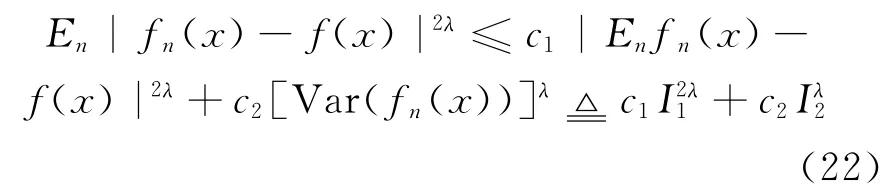
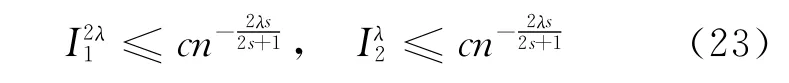
将（23）式代入（22）式可得结论（2）成立。

引理2 令R（G）和Rn分别由（13）式和（18）式给出，则

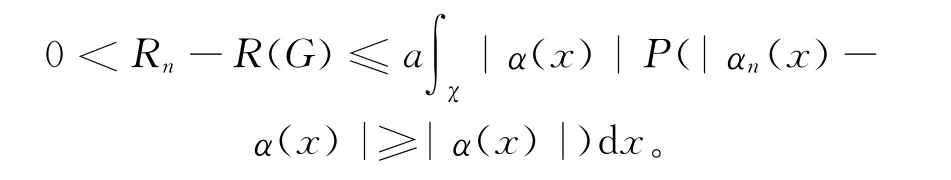
证明 见文献［1］引理1。

引理3 设φ（x）和φn（x）分别由（10）式和（15）式定义，其中X1，X2，…，Xn为独立同分布的样本，则对0＜λ≤1，有

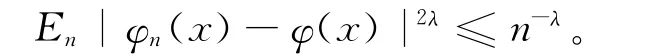
证明 由于

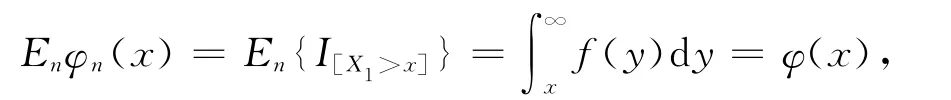
故φn（x）为φ（x）的无偏估计，由Jensen不等式可知：

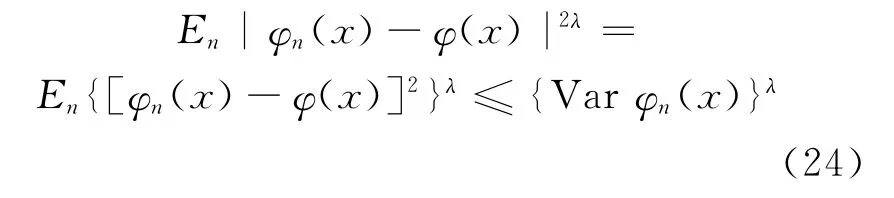
其中

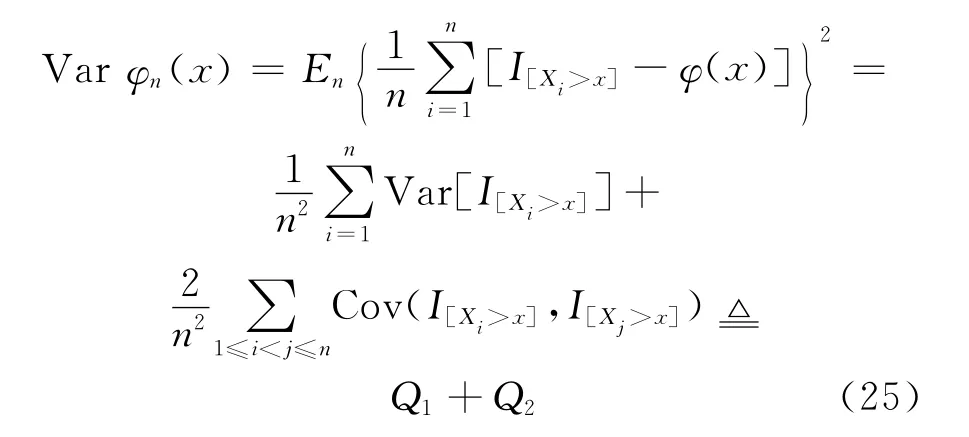
由于X1，X2，…，Xn为独立同分布r.v，故对一切i≠j，j＝1，2，…，n，有

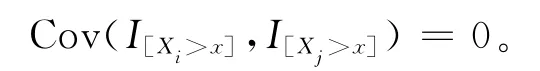
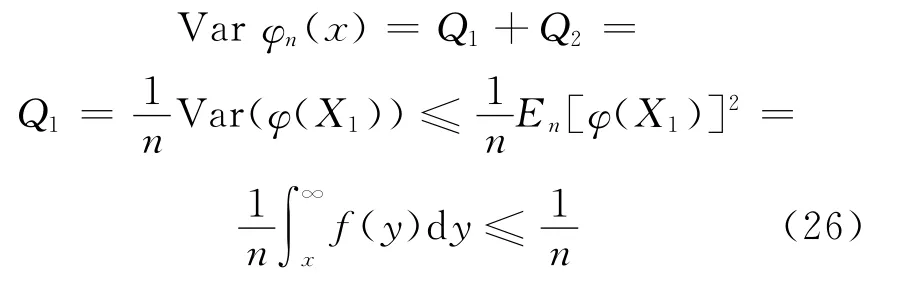
故由（25）式可知：将（26）式代入（24）式，引理得证。

2 EB检验函数的渐近最优性及收敛速度

定理1 设δn（x）由（17）式给出，其中X1，X2，…，Xn为独立同分布样本序列。假定条件（1）、条件（2）成立，若E（θ）＜∞且f（x）连续，则当时有：

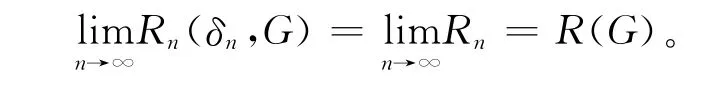
证明 由引理2可知：

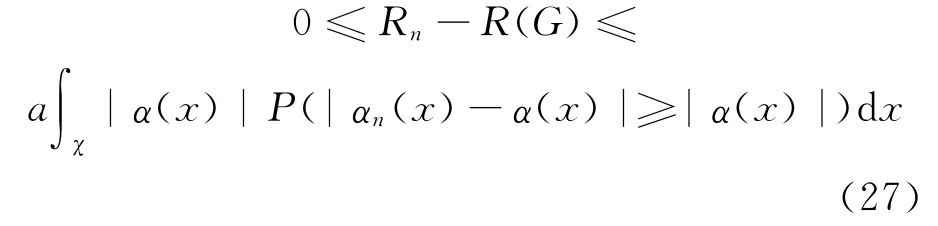
记Bn（x）＝｜α（x）｜P（｜αn（x）－α（x）｜≥｜α（x）｜），显见Bn（x）≤｜α（x）｜。由（11）式可知：

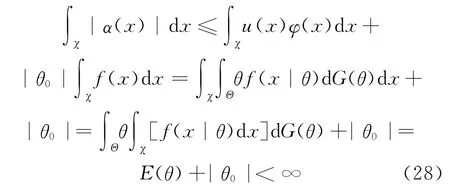
由控制收敛定理，可知：

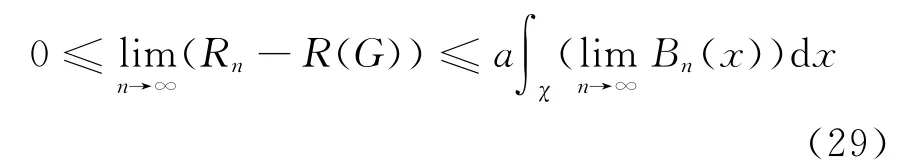
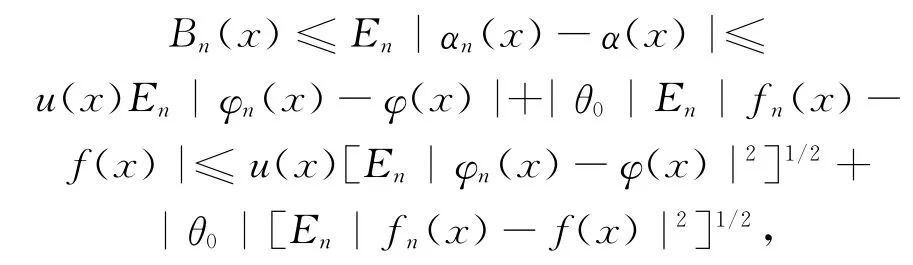
再由引理1和引理3可知，对任何固定的x∈χ有：

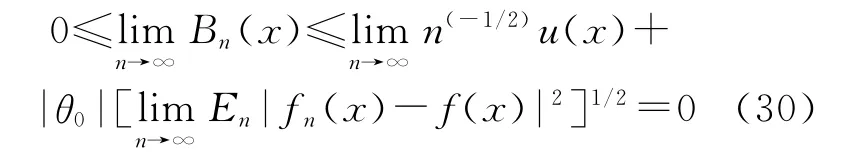
将（30）式代入（29）式，定理得证。

定理2 设δn（x）由（17）式定义，其中X1，X2，…，Xn为独立同分布的样本序列，且假定条件（1）和条件（2）成立，若0＜λ≤1，有

（1）f（x）∈Cs，α。

（2）∫χ｜α（x）｜1－λuλ（x）d x＜∞。

（3）∫χ｜α（x）｜1－λd x＜∞。

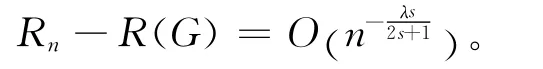
其中，s＞1为给定的一个正整数。

证明 由引理2和Markov不等式，可知：

由引理3和条件（2）可知：

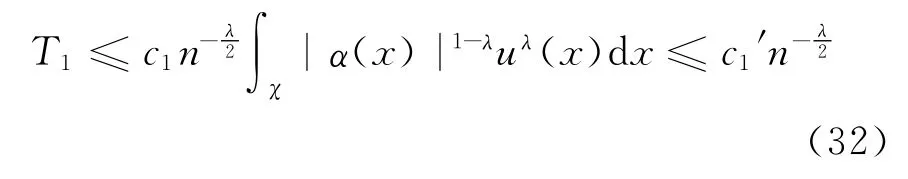
由引理1和定理1可知：

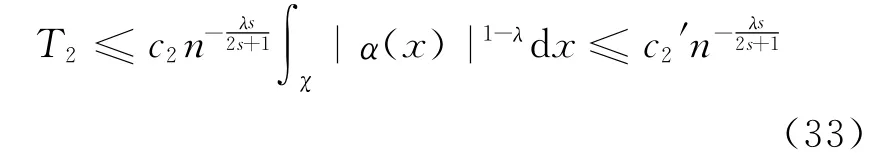
将（32）式和（33）式代入（31）式，定理得证。

3 例 子

为了说明适合文中定理条件的Weibull族和先验分布是存在的，在（1）式中，令m为给定正整数，其中，取θ的先验分布为：

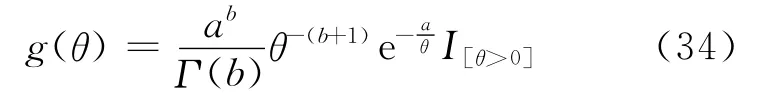
a和b为已知常数，且a＞0，b＞1，所以有：

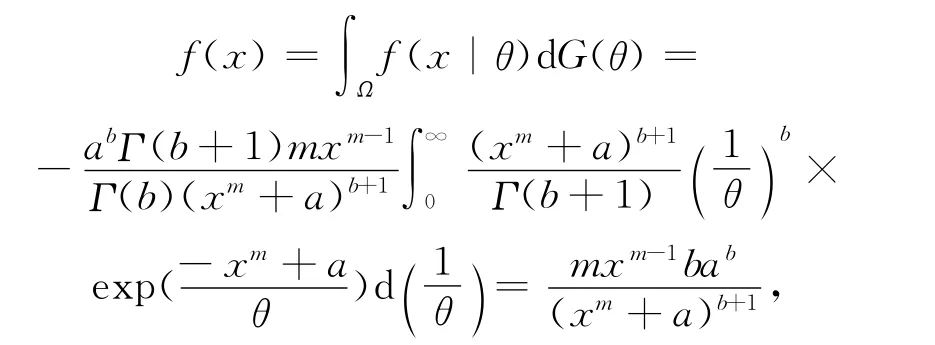
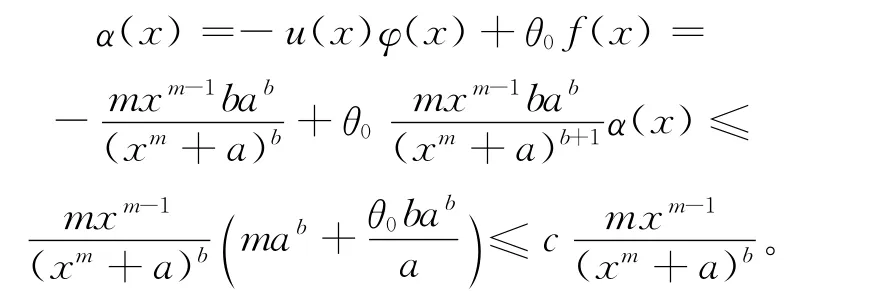
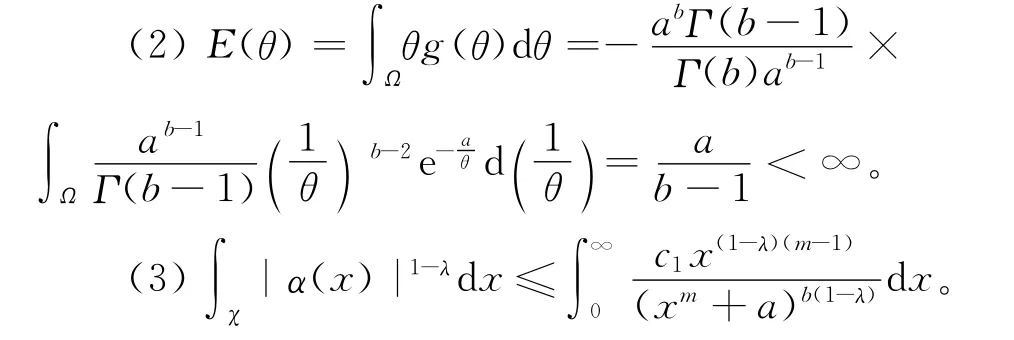
由于a＞0，b＞1，该积分为第1类广义积分，当mb（1－λ）－（1－λ）（m－1）＞1，即0＜λ＜m（b－1）／［m（b－1）＋1］，上述积分收敛。

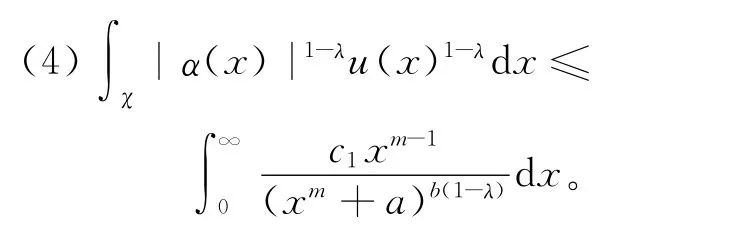
类似（3），当mb（1－λ）－（m－1）＞1，即0＜λ＜（b－1）／b，上述积分收敛。

由（1）～（4）可知，定理1和定理2的条件均成立。故有下述重要结论。

定理3 对Weibull分布（1）式先验分布由（34）式给出，其中a＞0，b＞1，m为任意固定正整数，则定理1成立，又若0＜λ＜（b－1）／b，则定理2成立。

［1］ Johns M V，Jr，Van Ryzin J.Convergence rates in empirical Bayes two－action problems 2：continuous case［J］.Ann Math Statist，1972，42：937－947.

［2］ Van Houwelingen J C.Monotone empirical Bayes test for the continuous one－parameter exponential family［J］.Ann Statist，1976（4）：981－989.

［3］ Liang Tachen.On empirical Bayes tests in a positive exponential family［J］.Journal of Statistical Planning and Inference，2002（3）：169－181.

［4］ Liang Tachen.On optimal convergence rate of empirical Bayes tests［J］.Statistics ＆Probability Letters，2004，68：189－198.

［5］ 魏 莉，韦来生.刻度指数族参数的经验Bayes检验问题［J］.中国科技大学学报，2004，34（1）：1－10.

［6］ 孙荣恒.应用概率论［M］.第2版.北京：科学出版社，2006：87－89.

［7］ 邓永录.应用概率及其理论［M］.北京：清华大学出版社，2005：43－44.

［8］ Singh R S.Empirical Bayes estimation in Lebesgue exponential families with the rates near the best possible rate［J］.Ann Statist，1979，7：890－902.

［9］ 凌能祥，杜雪樵.NA样本下单边截断型分布族位置参数的Bayes估计［J］.合肥工业大学学报：自然科学版，2002，25（5）：743－747.

［10］ 陈家清，刘次华.线性指数分布族参数的经验Bayes检验

问题［［J］.系统科学与数学，2008，28（5）：616－626.