GM(1,1)模型的改进与应用

谢臣英，尹方平

(广东机电职业技术学院，广州 510515)

0 引言

在灰色系统理论的应用中，预报或预测已成为灰色系统理论的一个最活跃的领域。在预测领域内，由于小样本、贫信息不确定性系统的大量存在，GM（1,1）模型作为灰色预测理论的核心，得到了广泛的应用[1][2]。但GM（1,1）模型也存在一些预测精度不高的情况，因此，对GM（1,1）模型进行深入仔细的研究，找出影响GM(1,1)模型精度及适应性的关键因素，提高GM（1,1）模型的精度及其适应性，具有非常重要的理论意义和实际意义。对GM（1,1）模型进行改进，大致可以分为三类：（1）对模型的参数估计方法的改进；（2）对模型背景值的改进；（3）对模型的初始条件的改进。

针对模型的初始值选取问题，在原有初始值选取的基础上，出现了多种改进方法的讨论[3～5]。本文拟提出一种修正初值法来提高模型的精度，对以x(1)(n)为初始条件的GM模型进行改进，使所建的模型的精度大为提高，并将通过具体的实例验证模型的实用性与可靠性。

1 改进的以x(1)(n)为初始条件的GM模型

1.1 传统的GM(1,1)模型

则一次累加后生成的1-AGO序列X(1)为：

Z(1)为X(1)的紧邻均值生成序列；

其中a和b为待确定的常数。a为发展系数，其大小及符号反映了X(0)(k)及X(1)(k)的发展态势。b为系统的灰色作用量，它是从背景值挖掘出来的数据，反映数据变化的关系。灰色作用量的存在是灰色建模与一般建模的本质区别，是系统内涵外延化的表现，是灰色系统重要内涵开发的表现。

2.2 以x(1)(n)为初始条件GM模型

以x(1)(n)为初始条件的GM模型是根据新信息优先原理和最少信息原理提出的灰色GM模型的一种改进的方法，它主要用于对复杂系统某一主导因素特征值的拟合和预测，以揭示主导因素变化规律和未来变化发展态势。

二十世纪六十年代初的一天凌晨，几百名警卫在柏林勃兰登堡门的分界线上各就各位，一道横贯东德和西德的冰冷墙壁隔绝了人们的交往。1984年，艺术家特里·诺尔趁守卫不注意，偷偷在灰白的柏林墙上涂鸦，开启了柏林墙的彩色生涯。十几年里，特里·诺尔和其他艺术家用长达一公里的涂鸦把柏林墙变成了艺术品，寄托了人们美好的愿望。冷战结束后，柏林墙被推倒，但在艺术家们的奔走下，涂鸦的部分被保留下来，这就是著名的“东边画廊”。

其法方程组为：

由白化方程的离散解不难得：

灰色微分方程x(0)(k)+az(1)(k)=b的时间响应序列为：

还原值为：

从上述模型可以看出，GM（1，1）模型的拟合和预测精度不但跟a,b有关，还跟x(1)(n)的取值有关。因此合理的选择初值对于提高模型的预测精度有着重要的作用。

1.3 增加扰动因素β的GM模型

为了获得最优的拟合曲线，提高模型的建模精度，不妨对模型的初始条件x(1)(n)增加扰动因素β，以x(1)(n)+β作为模型的初始条件。

将该初值代入

其中：

为了求出指标函数值最小时的待辨识参数β，先用如下梯度法求取dJ dβ=0。求得

2 实例分析

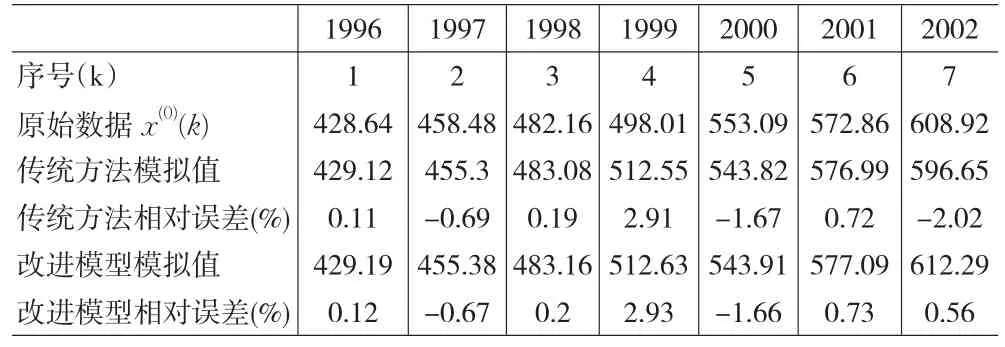
表1 模型值比较表 （单位：k w：h）

续表1

2.1 上海市发电量的检验性预测

现用本文提出的方法建立1996～2009年我国上海市的发电量《上海统计年鉴－2010》的GM（1，1）模型[6]，用matlab软件针对传统的GM（1，1）方法建立的模型和改进的模型分别进行仿真计算，结果如表1所示。

利用此模型进行预测上海市2010年发电量，即当原始序列k=15时，原GM（1，1）模型的预测值为x(0)(15)=847.59，改进的模型的预测值为x(0)(15)=856.48。

3.2 2008～2011年国内生产总值预测

笔者根据《中国统计年鉴－2010》[7]的数据建立灰色模型，对1999年至2009年数据进行分析，并对2010年至2011年GDP进行预测，结果如表2所示。

3 结束语

表2 GDP预测值 (单位：亿元)

续表2

本文在GM（1，1）灰色模型的基础上，提出了一种增加扰动因素β修正初值法来提高模型的精度，大大弱化了干扰因素，揭示了系统的运行规律，使得模型更为稳定。该方法保留了GM（1，1）模型建模计算简便和易于应用的优点，不存在复杂的计算。从实例分析上看，该方法能得到比原GM（1，1）模型更高的精度和适应性，无论在微观经济还是宏观经济上，都具有重要的理论价值和实践意义。

[1]刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京：科学出版社,2004.

[2]张圆刚,王心源.基于灰色系统理论经济视域下的农村居民出游可行性分析[J].经济问题探索,2008,(11).

[3]Deng Ju Long.Solution of Grey Differential Equation forGM(1,1|τ,r) in Matrix Train[J].The Journal of Grey System，2002,14(1).

[4]王义闹,刘光珍,刘开第.GM（1,1）模型的一种逐步优化直接建模法[J].系统工程理论与实践,2000,20(9).

[5]党耀国,刘思峰,刘斌.以x(1)(n)为初始条件的GM模型[J].中国管理科学,2005,13(1).

[6]李俊峰,戴文战.GM(1,1)改进模型的研究及在上海市发电量建模中的应用[J].系统工程理论与实践,2005,3(3).

[7]中华人民共和国国家统计局.中国统计年鉴2010[M].北京：中国统计出版社,2010.