磁流变减振系统的双谱分析研究

张福江，李丽娜

(福建工程学院机电及自动化工程系，福州350108)

磁流变液(Magnetorheological fluid，简称MRF)是一种智能软物质，具有强度高、黏度低、耗能小、温度稳定性好、对制造过程中产生的杂质不敏感等特点［1］.在外加磁场作用下，能以毫秒级速度从液态转化成半固态或固态，且这种过程是连续的、可逆的、可控的.由它制成的可调阻尼器，结构简单、响应快、动态范围广、耐久性好、不变质、阻尼力大、噪音小.

由于磁流变效应是非线性的，且振动系统的结构不对称性，外界干扰为非高斯过程.目前，对非线性、非高斯过程的磁流变振动的研究很少，多采用功率谱等传统信号处理方法，很难从根本上解决该类问题.高阶谱有很强的消噪能力，是分析非高斯信号的有力工具，可以从更高阶概率结构表征随机信号，能弥补二阶统计量(功率谱)不包含相位信息的缺陷，定量地描述非线性相位耦合度，理论上能完全抑制高斯噪声.实际应用中，采用双谱分析就可以满足磁流减振系统分析要求.

1 高阶谱分析原理

高阶谱用累积量定义，因此又被称为累积量谱.设{xn}为一个零均值的k阶随机平稳信号，定义{xn}的k阶联合累积量为［2］:

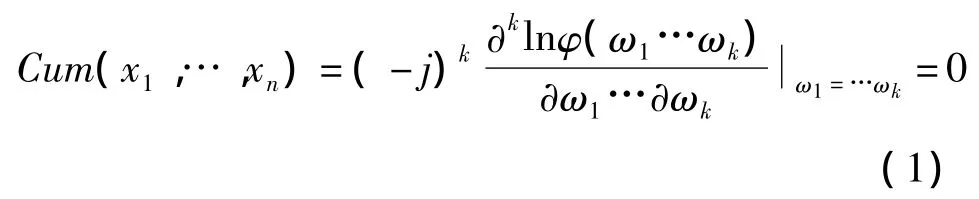
若高阶累积量Cumkx(τ1…τk－1)满足边界条件:

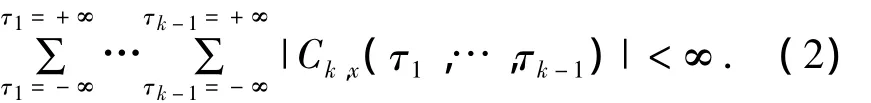
则随机信号{xn}的k阶累积量谱定义为k阶累积量的(k－1)维傅里叶变换，即:

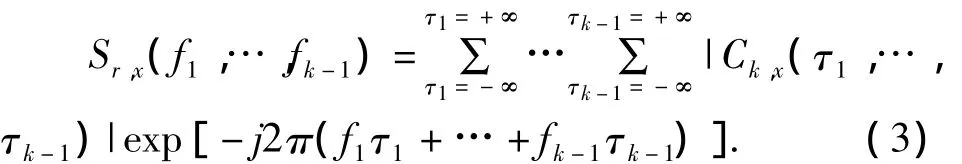
当k=2时，定义为二阶谱－功率谱:

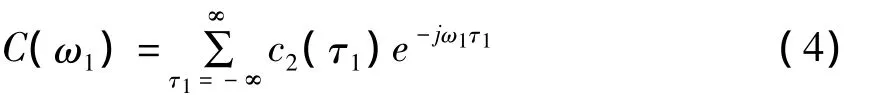
当k=3时，定义为三阶谱－双谱:

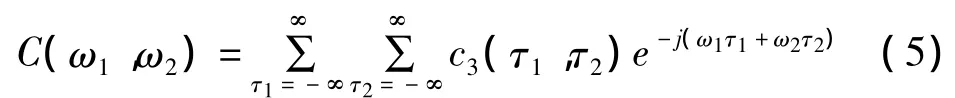
当k=4时，定义为四阶谱－三谱:

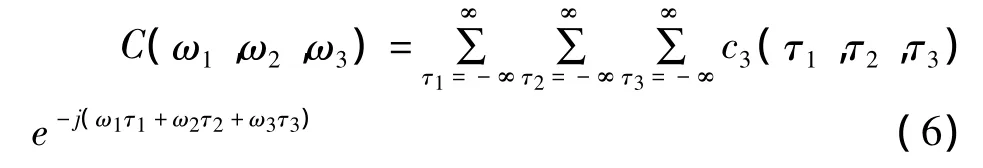
对比高阶谱表达式(3)与式(4)、式(5)可知:功率谱是实数，不包含相位信息，而高阶谱是复数，保留了系统信号的非线性信息和相位信息，可判别系统中是否存在非线性及非线性程度.W·B· Collis［3］对高阶谱的物理意义提出了近似的解释，二阶累积量是频域上的信号方差，三阶累积量是频域上的信号歪度，四阶累积量是频域上信号峰度.可以得出，高阶谱能够定量地描述信号非对称、非线性的特性.

2 实验部分

实验设计及装置如图1所示，磁流变阻尼器对电信号的响应可以达到数十毫秒级，为达到快速减振效果，要求高的信号采样率.

图1 实验设备实物图

实验方法与过程:采集振动台位移信号、加速度信号和阻尼器内部工作区温度信号，经调理和去噪声后通过数据采集卡输入计算机;在基于Lab-VIEW虚拟仪器控制平台上进行处理、分析和显示，得到振动速度和位移幅值，根据具体的减振要求(如幅值控制)和相关参数(系统结构、磁流变材料特性等)，计算出需要的控制电流大小;用GBIP方式，通过数据采集卡和GBIP传输电缆调整输出电流源，控制阻尼器的阻尼力实现减振.

3 实验数据分析

3.1 信号预处理

双谱分析的信号源为试验台振动信号的白噪声，因此在进行双阶谱分析前，需对信号进行预处理，将采集到的数据进行滤波、消除趋势项，进而获取白噪声信号.图2是磁流变振动系统的采样信号，图3是通过中值滤波［4－5］后获得的系统白噪声信号.

经处理后的数据符合LabVIEW虚拟仪器控制平台计算要求，且保持了非线性特征和相位信息.

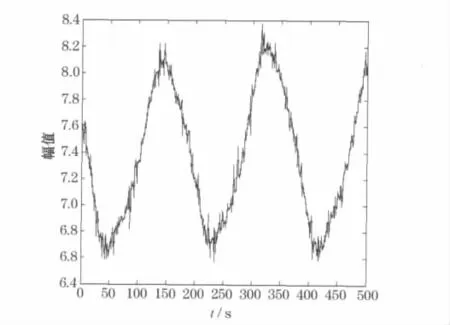
图2 采样信号

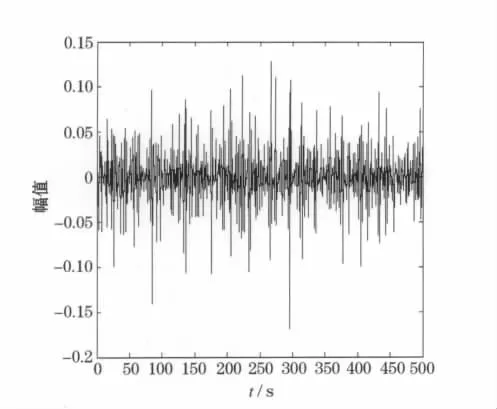
图3 中值滤波后信号

3.2 图谱分析

3.2.1 双谱和等高分析

图4、5是磁流变减振器不外加电流时，采样信号的双谱图和等高线图，图6、7是磁流变减振器外加电流为1A时，采样信号的双谱图和等高线图.

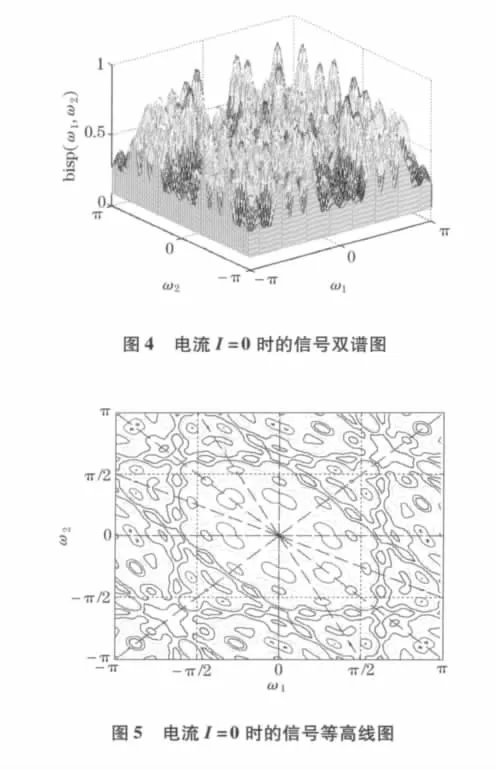
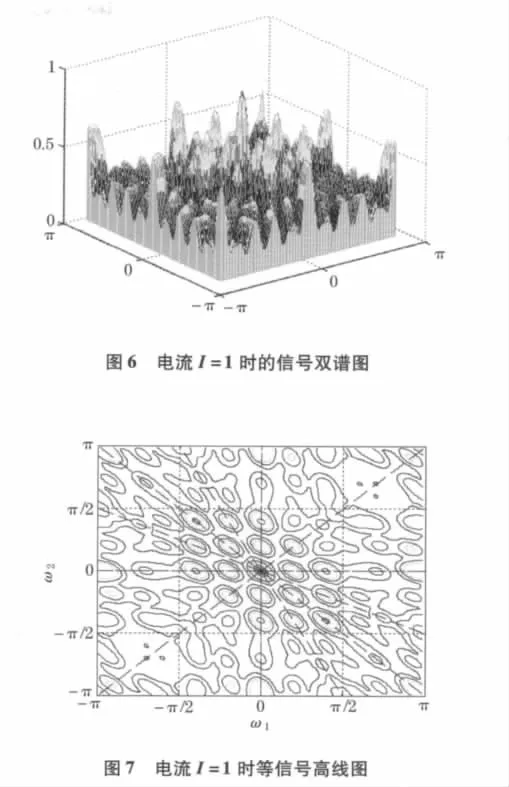
对比分析发现，在没有输入电流，即I=0 A的状态下，磁流变减振系统的振动耦合现象比较剧烈，存在较多的谱峰高点;当I=1 A时，减振系统振动程度减小，谱峰高点分布减少，且分布区域较无电流输入时发生很大变化.

3.2.2 相位分析

对应两种实验状态的相位分析如图8、9所示.

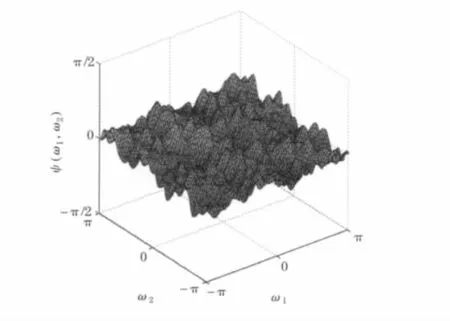
图8 电流I=0 A时的信号相位谱

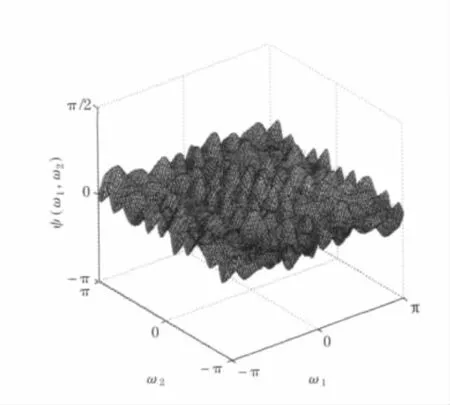
图9 电流I=1 A时的信号相位谱

明显可见，I=0 A时磁流变减振相位落差较大，且分布不均匀;而I=1 A时，相位分布相较之下趋于均匀.说明磁流变减振系统存在比较明显的二次相位耦合，即明显的非线性现象，主要是由减振台滚动轴承、齿轮等零件存在调制或不对中以及油缸的复杂润滑条件等因素造成的.

3.2.3 谱峰分析

为进一步分析电流调节对系统振动的影响程度，对数据双谱谱峰处进行了切片分析［2－6］，研究谱峰变化规律.表1为计算得出的双谱谱峰位置和幅值.

表1 双谱谱峰坐标及幅值

其结果表明，电流I=0 A，在ω1=44和ω1= 86时出现双谱峰情况;电流I=0.5 A，在ω1=55和ω1=75时也会出现双谱峰情况，且双谱峰逐渐向中间靠拢.

图10是在此基础上画出的双谱位置图，“×”表示电流为0A时的谱峰位置，“O”表示电流为0.5 A时的谱峰位置，“*”代表电流大于0.5 A时谱峰的位置.

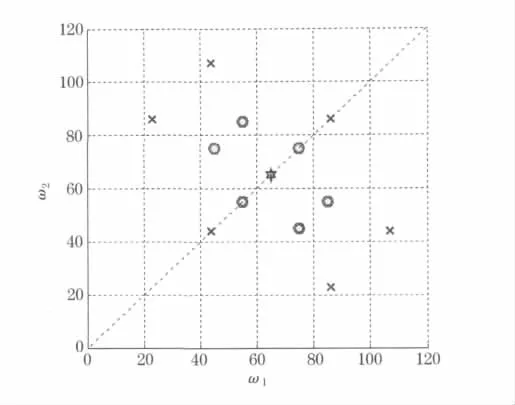
图10 双谱位置图

结合表1和图10，分析得出:1)电流I=0 A和I=0.5 A时，双谱各有6个谱峰;电流大于0.5 A时，双谱只有一个谱峰，且谱峰位于ω1=ω2=65处.2)从谱峰位置分布来看，对应每一电流，谱峰位置关于直线y=x对称;从谱峰幅值大小来看，虽然表现出高低起伏的现象，但随着电流的增加，幅值呈现下降趋势.说明，随电流的增加，能量逐步减少.3)随电流的增加，谱峰表现出向中心点(65，65)聚集的趋势.电流I=0 A时，谱峰在图10的最外沿;电流I=0.5 A时，谱峰位于内侧;而当电流大于0.5 A时，谱峰则位于中间(65，65).说明，随电流的加大，能量的分布表现出明显的集中趋势.

4 结语

应用高阶谱信号分析原理，采用双谱分析方法，结合现代统计学和计算机数据处理技术，研究了磁流变减振系统非线性特性规律.实验结果表明，磁流变减振系统的谱峰分布规律表现出非常明显的对称性和收敛性，即随着电流的增加，谱峰位置逐渐向中间靠拢，并最终收敛于原点，而且每一个电流的谱峰位置都保持严格的对称性.可以得出，用双谱分析方法判别系统的非线性特征，尤其是在相位信息的展现方面相对传统的功率谱分析具有绝对优势.

［1］ YANG G Q，JUNG H J，SPENCER B F.Dynamic Modeling of Full－Scale MR Dampers for Civil Engineering Applications［R］.US－Japan Workshop on Smart Structures for Improved Seismic Performance in Urban Region，Seattle，WA，2001:14－16.

［2］ 张贤达.时间序列分析［M］.北京:清华大学出版社，1996.

［3］ COLLIS W B，WHITE P R，HAMMOND J K.Higher－order spectra:the bispectrum and trispectrum［J］.Mechanical System and Signal Processing，1998，12(3):375－395.

［4］ BURIAN A，KUOSMANEN P.Tuning the smoothness of the recursive median filter［J］.IEEE Transaction on signal processing，2002，50(7):1631－1639.

［5］ 罗四倍，张保会，曹瑞峰，等.基于中值滤波的超高速暂态量方向元件［J］.中国电机工程学报，2007，27(34):64－69.

［6］ HINICH M J，WOLINSKY M.Normalizing bispectra［J］.Journal of Statistical Planning and Inference，2005，130(1－2): 405－411.