Vague软集的相似度量及其应用

王 昌

（西北大学a.数学与科学史研究中心；b.数学系,西安 710127）

0 引言

Zadeh在1965年首先开创了Fuzzy集理论[1]，但由于Fuzzy集的隶属函数值是一个单一的值，它不能同时表达支持和反对的证据，为此，Gau和Buehrer于1993年提出了Vague集的概念[2],它是一种Fuzzy集的推广[3],也是一种直觉的模糊集[4]。随后的几十年，Vague集理论得到了不断地发展和完善，在包括数学、自动控制、智能系统等众多领域得到广泛地应用[5-6]。然而，这两种理论都有一个共同的不足之处，就是它们都只能处理一部分不确定性信息，即参数工具理论的不充分。为解决这个问题，Molodtsov于1999年在文献[7]中引入了软集概念以克服这些不足，如今软集理论已被成功应用到众多的领域[8-9]。对于Vague集理论和软集理论的研究一直以来都主要集中在两个方面：一是研究两者各自的代数性质，另一方面则注重于它们各自在模式识别、不确定性推理等领域中的应用。可见所有这些研究都没能将两者结合起来，文献[10]依据Vague集和软集的现有理论，首先将两者的思想融合起来，提出了Vague软集的一些基本概念，并提出公开问题即研究Vague软集的潜在应用。文献[11]进一步给出了Vague软集的一些概念，并研究了与其相关的一些代数性质。本文在此基础上，给出了Vague软集间相似度量的公理化定义，同时引入了一种计算Vague软集间相似度量的公式，最后通过一个实例给出了Vague软集间的相似度量在模糊多目标决策系统中的应用，从而部分回答了文献[10]中提出的公开问题。

1 预备知识

定义1[2]令U是一个点（对象）的空间，其中任意的一个元素用x表示，U上的一个Vague集A用一个真隶属函数tA(x)和一个假隶属函数 fA(x)表示，tA(x)是从支持x的证据所导出的x的隶属度下界，fA(x)是从反对x的证据所导出的x的否定隶属度下界，tA(x)和 fA(x)将区间[0,1]中的一个实数与U中每一个点联系起来，即tA∶U→[0,1]；fA∶U→[0,1]，其中tA(x)+fA(x)≤1。称[tA(x),1-fA(x)]为x在A中的Vague值，记为A(x)，论域U上Vague集全体用V(U)表示。当U离散的时候，；当U连续的时候，x∈U。

定义2[7]设U是一个论域，P(U)是U的幂集，E是一个参数集，A⊆E,且：

F∶A→P(U)是一个映射,称(F,A)为U上的一个软集。

定义3[10]设U是一个论域，E是一个参数集，A⊆E,且F∶A→V(U)是一个映射，即∀e∈A,F(e)是U上的一个Vague集，称(F,A)为U上的一个Vague软集。用VSS(U)来表示。

例1令(F,E)为Vague软集，论域U={x1,x2,x3}表示决策者打算购买的三种不同的房子，参数集E={e1,e2,e3}= {房屋结构，房屋价钱，房屋面积}，Vague软集(F,E)表示对于购买者的吸引情况，若：

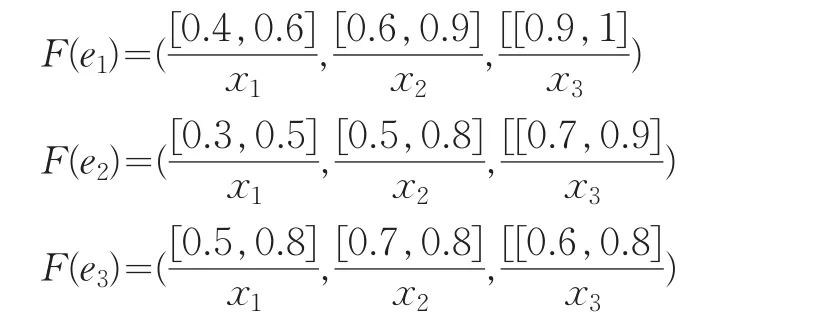
论域U上的参数集族{F(ei),i=1,2,3}即为Vague软集(F,E)，用矩阵形式表述如下：

2 Vague软集的相似度量

通过文献[12]可知，众多学者在研究Vague集的相似度量方面已经形成了一些共识，现在我们将这些共识进行整理改进，提出Vague软集(F,E)和(G,E)间的相似度量。

M((F,E),(G,E))应满足的定义：

定义4VSS(U)表示论域U上的Vague软集，E是一个参数集，(F,E),(G,E)∈VSS(U),函数M∶VSS(U)×VSS(U)→[0,1]称为Vague软集间的相似度量，如果其满足以下条件：

（1）有界性M((F,E),(G,E))∈[0,1]

（2）对称性M((F,E),(G,E))=M((G,E),(F,E))

（3）归一性M((F,E),(G,E))=1⇔(F,E)=(G,E)

（4）单调性(F,E)⊆(G,E)⊆(H,E),(H,E)∈VSS(U) M((F,E),(H,E))≤min(M((F,E),(G,E)),M((G,E),(H,E)))

通过Vague软集间相似度量的公理化定义，可知它是评价两个Vague软集间的相似程度的，显然，两个Vague软集间的相似度量越大，则这两个Vague软集越相似。

定理1设U={x1,x2,...,xn}是一个论域，E={e1,e2,...[,em}]是一个参数集，故(F,E)={F(ei)|i=1,2,...,m}是一个Vague软集族，称：

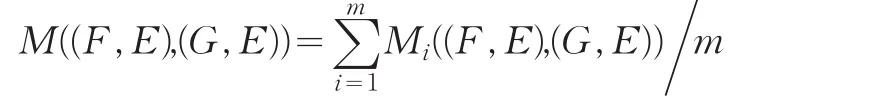
为Vague软集(F,E)和(G,E)的相似度量，如果H(F,[E)]满足定义4，这里：

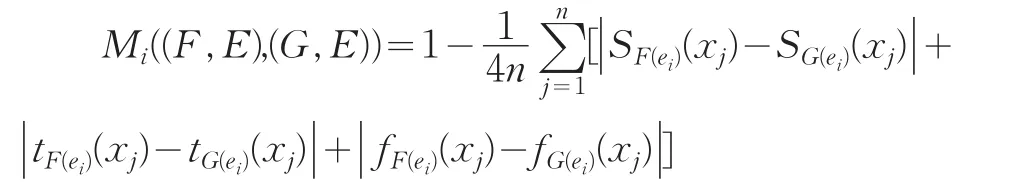
其中：SF(ei)(xj)=tF(ei)(xj)-fF(ei)(xj),SG(ei)(xj)=tG(ei)(xj)-fG(ei)(xj)分别叫做F(ei)和G(ei)的核，它表征对于参数ei来说，现有证据对元素xj支持和反对两种力量的对比，看作整体支持（肯定）度，SF(ei)(xj)∈[-1,1],SG(ei)(xj)∈[-1,1]。

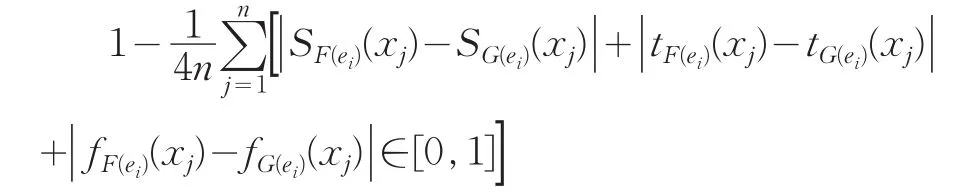
从而M((F,E),(G,E))∈[0,1]

（2）由于Mi((F,E),(G,E))=Mi((G,E),(F,E)),故：

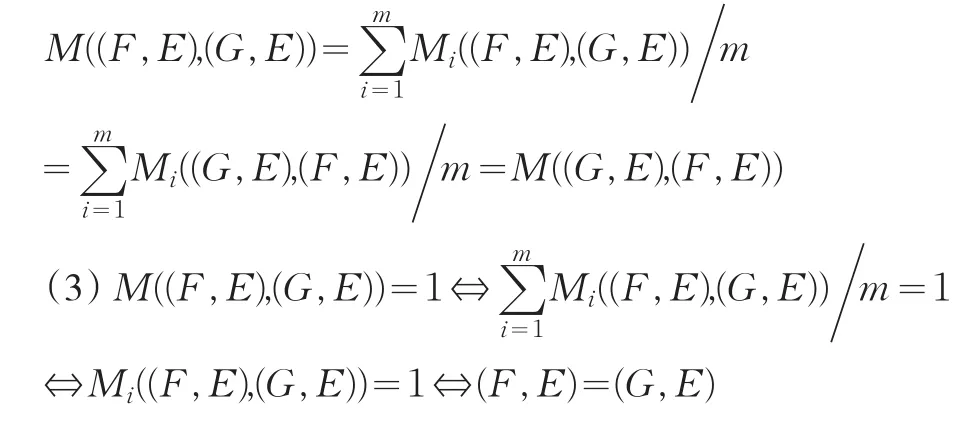
（4）由于(F,E)⊆(G,E)⊆(H,E),故：

tF(ei)(xj)≤tG(ei)(xj)≤tH(ei)(xj),fF(ei)(xj)≥fG(ei)(xj)≥fH(ei)(xj),即

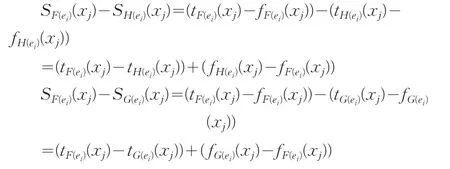
综上可知Mi((F,E),(H,E))≤Mi((F,E),(G,E))

从而M((F,E),(H,E))≤M((F,E),(G,E))

同理有M((F,E),(H,E))≤M((G,E),(H,E))

故M((F,E),(H,E))≤min(M((F,E),(G,E)),M((G,E), (H,E)))。

3 实例分析

例2假设一个房地产商有三种房子，这三种房子所具有的特性均以参数集

E={e1,e2,e3,e4,e5,e6}={面积大，结构好，价钱高，质量好，周围交通差，周围绿化好}表示，我们的论域U中仅包含两个元素，即“赞成”和“反对”，可表示为U={赞成，反对}。

现有一人打算在此处买一套房子，专家对最完美的房屋给出的Vague软集(F,E)的评价值如表1所示，其它三种房子的Vague软集的评价值分别如表2～4所示：

表1 最完美房子的VSS(U)

表2. 第一种房子的VSS(U)

表3 第二种房子的VSS(U)

表4 第三种房子的VSS(U)

通过计算，可得M((F,E),(G,E))≅0.575;M((F,E),(H,E))≅0.738;M((F,E),(P,E))≅0.517

由于第二种房子与最完美房子的Vague软集的相似度量值最大，故应该买第二种房子。

4 结束语

Molodtsov提出的软集理论为处理不确定信息提供了一种一般的方法，文献[10]首先引入Vague软集的概念，并研究了一些相关的性质，同时提出公开问题即研究Vague软集的潜在应用。本文在此基础上，给出了Vague软集的相似度量的公理化定义，并给出了一种计算Vague软集间相似度量的方法，最后通过一个实例说明了Vague软集的相似度量在模糊多目标决策系统中的应用。希望这些工作日后能成为Vague软集理论应用的有力工具。

[1]Zadeh L A.Fuzzy Sets[J].Information and Control,1965,8(3).

[2]Gau W L,Buehrer D J.Vague Sets[J].IEEE Transactions on System, Man and Cybemetics,1993,23(2).

[3]Deschrijver G,Kerre E E.On the Relationship between Some Exten⁃sions of Fuzzy Set Theory[J].Fuzzy Sets and Systems,2003,133(2).

[4]Deschrijver G,Kerre E E.On the Composition of Intuitionistic Fuzzy Relations[J].Fuzzy Sets and Systems,2003,136(3).

[5]Zhang Q S,Jiang S Y,Jia B G,et al.Some Information Measures for In⁃ terval-valued Intuitionistic Fuzzy Set[J].Information Sciences,2010,180 (24).

[6]Kumar A,Yadav S.P,Kumar S.Fuzzy Reliability of A Marine Power Plant Using Interval Valued Vague Sets[J].International Journal of Ap⁃plied Science and Engineering,2006,4(1).

[7]Molodtsovd D.Soft Set Theory—First Results[J].Computer and Mathe⁃matics with Applications,1999,37(4).

[8]Xiao Z,Gong K,Xia S,Zou Y.Exclusive Disjunctive Soft Sets[J].Com⁃puters and Mathematics with Applications,2010,59(6).

[9]Qin K,Hong Z.On Soft Equality[J].Journal of Computational and Ap⁃plied Mathematics,2010,234(5).

[10]Xu W,Ma J,Wang S Y,et al.Vague Soft Sets and Their Properties[J]. Computer and Mathematics with Applications,2010,59(2).

[11]王昌,袁敏.Vague软集的一些代数性质[J].计算机工程与应用, 2010,46(13).

[12]王昌.Vague集的模糊熵、相似度量和距离测度的关系[J].计算机科学,2010,37(10).