基于核仁的供应链合作收益分配研究
2012-03-12吴铭峰
吴铭峰
(1.河海大学商学院,南京 210098;2.江苏信息职业技术学院,江苏无锡 214153)
0 引言
供应链合作收益分配的研究,从竞争与合作的角度可以分为竞争性的收益分配和合作性的收益分配。竞争性收益分配的方法包括:按各种资源比例分配;使用委托代理机制进行分配;应用Stackelberg博弈模型、Nash博弈模型进行分配等。竞争性收益分配的方法大都不考虑供应链成员的集体理性、联盟理性和个体理性,供应链成员存在脱离供应链单干,或者部分供应链成员组成新的供应链以期获得更大收益的激励,不利于供应链的长期稳定。合作性收益分配的方法借鉴了合作博弈的思想,以联盟作为分析的单位,强调集体理性、公平和效率,将合作博弈的“解”概念作为收益分配的依据。从现有的文献来看,Shapley值得到较多应用。徐向阳和安景文等[1]在分析多人合作中的费用分摊问题时、赵晓丽和乞建勋[2]在研究煤炭企业合作利益分配问题时均使用了Shapley值作为分析工具。Shapley值是将收益按照参与人的边际贡献率进行分摊,参与人i所应当获得的收益等于该参与人对每一个他所参与的联盟的边际贡献的平均值。Shapley值的应用中存在较多的争议:(1)Shapley值可能不在于核配置中;(2)从福利经济学的角度看,Shapley值体现的是一种功利主义的“公平”;(3)从分配的时机上看,Shapley值法属于事先分配。这些问题的存在使得Shapley值的应用受到很大的限制[3]。而合作博弈中其余“解”的概念均未见应用。
本文尝试将合作博弈另一个重要的“解”概念——核仁,应用到合作收益分配的研究中,以由M个供应商和N个零售商组成的单层供应链为研究对象,在最大化供应链收益的情况下,通过计算核仁对供应链合作收益进行分配,为供应链合作收益分配的研究提供新的思路和方法。
1 问题描述
在市场中存在m个生产商和n个零售商组成的供应链联盟P,生产商根据自身的能力及需求来选择对应的零售商为其销售商品,而零售商通过为生产商提供服务来获取收益。为讨论方便,本文做如下假设:(1)生产商的生产的商品只能通过一个零售来进行销售;(2)零售商所提供的服务是不可分割的,即一个零售商只能同时为一个生产商销售商品。令M表示生产商的集合、N表示零售商的集合。对于每一对生产商i∈M和零售商 j∈N的组合() i,j∈M×N,存在一个正整数aij表示生产商i和销售商j进行合作时所产生的收益,收益矩阵为其中生产商获利为ui,销售商收益为表示生产商i的合作伙伴是销售商j。联盟P的收益由生产商和零售商合作时产生的收益总额决定,即v() P=本文的目标是在最大化供应链收益的情况下,通过计算核仁,将联盟的收益在生产商和零售商之间进行分配。
2 联盟收益最大化模型
在日常生活中经常遇到如下问题:有n项任务,有n个人可承担,由于每人的专长不同,各人完成不同任务的效率也不同,于是产生应指派哪个人去完成哪项任务,使完成n项任务的总效率高(或其他目标)的问题。这样的问题被称为指派问题。
最大化联盟P的收益也可以看作是指派问题,即存在m种商品需要进行销售,有n个零售商可以负责进行完成,由于每个销售商的专长、能力、效率等的不同,就存在指派哪个零售商销售哪种商品可以使得联盟收益最大的问题。
指派问题适用于解决m=n的情况,由上文可知参与供应链联盟的生产商和零售商的人数存在m≠n的可能性,为讨论的方便我们引入虚拟参与人,以数字“0”进行标记,并允许他们出现在任意的生产商和零售商合作组合中,组合表示空组合表示生产商表示零售商,此时供应链联盟。包含虚拟参与人的组合收益为0,即a00=ai0=a0j=0,此时收益矩阵为
最大化收益联盟收益可以转换为如下0-1规划模型
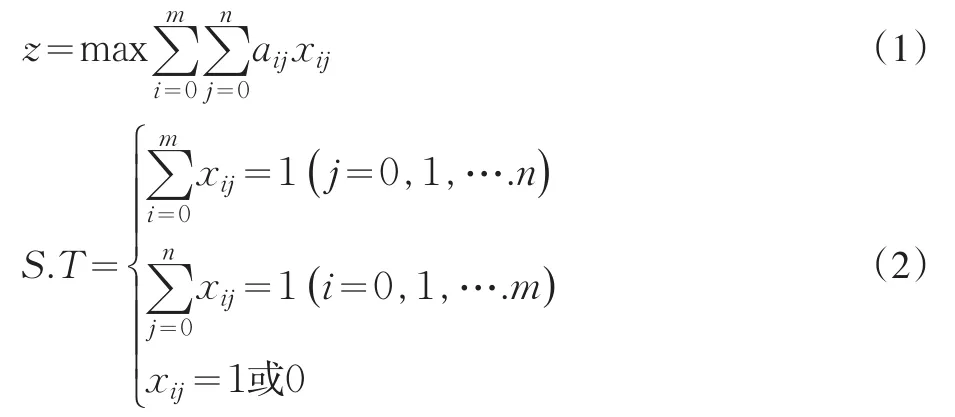
目标函数z的值为联盟P的收益,式(1)表示每个零售商只为一个生产商服务,式(2)表示每个生产商只选择一个零售商销售商品,决策变量xij表示生产商和零售商的合作情况,当xij=1时,组合( ) i,j进行合作,零售商 j完成生产商i的商品销售任务。z取得最大值时联盟P的收益最大。使收益联盟最大的指派称为最优指派σ。
3 供应链合作伙伴收益分配的核仁解
3.1 核仁的定义
核仁(nucleolus)是由Schmeidler首先提出的概念,他定义核仁为在所有满足有效性配置的集合B中,存在唯一配置γ,使得∀x∈B,,则γ被称为博弈的核仁,并证明了每一个合作博弈都存在非空的核仁,当核存在时,核仁必定包括在核中[4]。
Maschler,Peleg和Shapley针对类似于“m个生产商和n个零售商”的双边市场问题给出核仁的另一个定义:令σ为联盟的的最优指派。构建联盟上的分割序列,其中Σ0⊃…⊃Σn+1,得益向量序列X0⊃…⊃Xn+1,则通过如下迭代过程得到核仁[5]:
首先,令Δ0=σ,
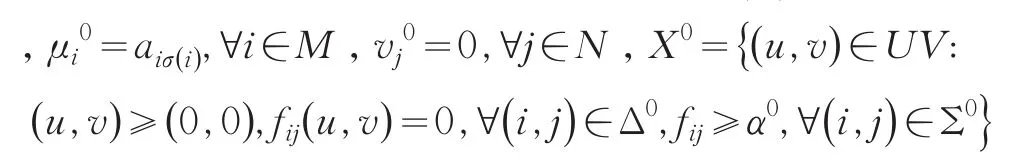
当r=0,1,2,…,n时,回归过程如下:


其中,n是使得Σr≠φ成立时,r的最大值,集合Xn+1是博弈A( ) M,N 的按字典排序的中心。Maschler,Peleg和Shapley证明了如下结论:(1)该博弈的按字典排序中心只有一个点;(2)该博弈的按字典排序中心和博弈的核仁重合[5]。本文今后的讨论与计算中将以Maschler,Peleg和Shapley给出的定义为主。
3.2 核仁解的优点
与Shapley值相比,核仁有着显著的优势:(1)Schmeidler、peleg等先后证明了合作博弈中核仁的存在性,只要合作博弈的核存在,那么核仁必然在核中且唯一[4]。(2)核仁是从平均主义的角度来衡量各个不同的联盟S所能带来的福利,衡量的标准为联盟的剩余e(x ) ,S。令N={ }
1,2,…,n表示参与人集合,v() S表示联盟S中参与人相互合作所能得到的收益,对于∀x∈B以及S⊂N,定义,可见当收益分配为x时,e(x ,S)越小,联盟S的满意度越高。剩余可以理解为给联盟S带来的超过“机会剩余”的额外好处,它通过最大化最小剩余,即来获得最终的收益分配,体现了平均主义的公平性。
3.3 核仁的计算
核仁的计算往往涉及到求解包含多个变量和多个约束方程在内的最小化线性规划问题,在Kohlberg[6]提出的方法中按照剩余的大小给予不同的权重,虽然能够得到解,但是会导致很庞大的线性规划问题。Owen[7]做出了改进但面对n个参与人的问题时,最小化线性规划问题中也包含了2n+1+n个变量和4n+1个约束条件的。与Shapley值相比核仁的计算较为困难。本文通过如下方法求解核仁[8]。
假设σ是联盟的( ) M,N,A 的最优指派。令r=0,


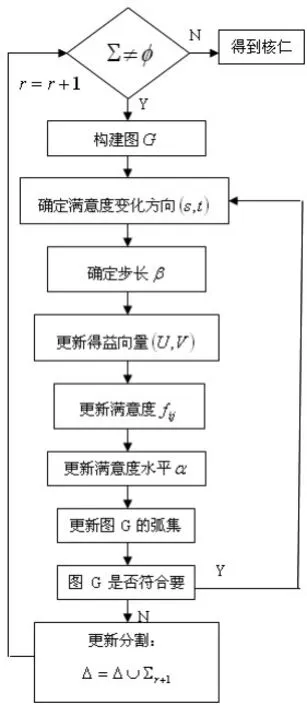
图1 核仁的计算步骤
(ⅰ)对于H中所有没有入弧的点p,令ℓ() p=k。在H中将所有这些点以及由这些点出发的弧全部删去。令k=k+1。重复操作(ⅲ),直到H没有点存在。完成算法(ⅲ)后,令
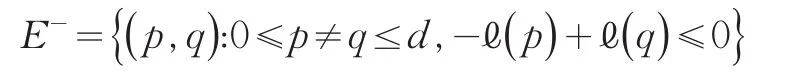
(5)更新收益向量( ) U,V 。在最优指派σ下,生产商i和销售商 j进行合作时所产生收益aij,其中生产商获利为ui,销售商收益为vj=aij-ui,得到收益向量,并根据式进行更新。
(6)更新满意度 fij。满意度 fij表示,在收益向量为时,任意组合的满意程度,满意度依下式改变:
(ⅱ)检验节点0是否有入弧,如果有就将弧的出点融入到节点0,保留其他的弧。也就是,如果,从E删除点p和弧。在上述情况下,如果,那么增加弧删除弧;如果,增加弧删除弧
(ⅲ)图G中是否存在回路,如果存在则将圈中点所有点合成一个点,并继承这些点的所有入弧和出弧,也就是如果,在D中增加一点p,将C中所有点和弧全部删除。
经过(ⅰ)、(ⅱ)两步检验后得到的图G为符合要求的图。
(9)更新分割Σ=ΣΣr+1,Δ=Δ∪Σr+1。
(10)当Σ≠φ成立时,得到的收益( ) U,V ,即为最大化联盟收益时,生产商和零售商的核仁。
4 结论
本文使用合作博弈的核仁解,对包含m个生产商和n个零售商的供应链联盟的合作收益分配问题进行了分析。通过实证分析可以看到,本文使用的方法能够实现预期目标,在最大化联盟收益的情况下,求得合作博弈的和核仁解,将收益在联盟成员之间进行分配,体现了平均主义的公平性,为供应链合作收益分配问题的研究提供了新的方法。在今后的研究中,将放宽对生产商和销售商合作伙伴数目的限制,使问题更贴近实际。
[1]Schmeidler D.The Nucleolus of a Characteristic Function Game[J].SI⁃AM J.Appl.Math,1969,(17).
[2]Maschler M,Peleg B,Shapley LS.Geometric Propertise of the Kernel,Nu⁃cleolus,and Related Solution Concepts[J].Mathematics of Operations Research,1979,(4).
[3]Kohlberg E.The Nucleolus as a Solution of a Minimization Problem[J]. SIAM J.Appl.Math,1972,(23).
[4]Owen G.A Note on the Nucleolus[J].International Journal of Game The⁃ory,1974,(3).
[5]Tamas Solymosi.An Algorithm for Finding the Nucleolus of Assignment Games[J].International Journal of Game Theory,1994,(23).
[6]马世华,王鹏.基于Shapley值的供应链合作伙伴间收益分配机制[J].工业工程与管理,2006,(4).
[7]徐向阳.供应链管理中风险分担与利益分配机制研究[J].华中科技大学学报,2004,(5).
[8]赵晓丽,乞建勋.供应链不同合作模式下合作利益分配机制研究—以煤电企业供应链为例[J].中国管理科学,2007,(8).
