PAC-3拦截弹六自由度反导建模与拦截仿真分析
2012-03-03刘芳陈万春
刘芳,陈万春
(北京航空航天大学宇航学院,北京 100191)
引言
本文针对PAC-3拦截弹拦截战术弹道导弹的特点,进行了六自由度动力学建模[4],并对拦截弹初、中、末制导3个飞行状态分别设计了不同的导引控制策略[5-8]。利用VC 6.0软件进行了面向对象的全弹道拦截仿真程序设计,面向对象的程序设计方法可实现多拦截弹拦截目标的功能,并为拦截仿真程序向攻防对抗大系统内嵌入提供了便利条件。然后,对惯性再入目标进行了多拦截弹拦截仿真,给出了拦截曲线及姿控发动机消耗等仿真结果。最后,通过5 000次单拦截弹拦截仿真结果,利用支持向量机(SVM)方法得到了拦截弹的可拦截布防区结果。
1 拦截弹模型的建立
1.1 弹体六自由度模型
对于滚转导弹来说,弹体坐标系上的动态会不断变化。为便于控制器的设计,将导弹各动态表示在半弹体坐标系上,其x轴与弹体坐标系重合,y轴垂直于地面坐标系的xOz平面。在半弹体坐标系上导弹绕质心转动的动力学方程为:

式中,下标b表示半弹体坐标系;Mxb0,Myb0,Mzb0为拦截弹非控制力矩;,为力矩系数对舵偏角δxb,δyb,δzb的偏导数;其它符号的含义见文献[4]。
为了便于利用动态逆方法设计导弹自动驾驶仪,避免最小相位情况的发生,将导弹质心运动的动力学方程表示为半弹体坐标系上的气动角形式:


1.2 拦截弹与目标相对运动模型
导弹与目标相对运动模型建立在惯性坐标系中。两者之间距离的3个分量为:

式中,下标t,m分别表示目标和拦截弹。
则导弹与目标的距离和相对速度为:

1.3 制导系统模型
PAC-3导弹系统采用的复合制导体制为:初段程序自控,中段指令修正,末段弹上主动制导。
总体规划层面,应强调总量控制及布局引导。在总体规划的绿色生态专项规划内容中,建立全市近期绿色建筑发展总量预测,提出规划期末绿色建筑与新建建筑比指标,同时研究全市绿色建筑重点发展区域及绿色生态示范区建设目标。
初制导:采用自主式程序制导。PAC-3导弹采取38°固定仰角发射的方案,出筒时速度矢量很可能没有指向预测命中点,因此需要将导弹速度矢量调整到发射点与预测命中点连线上。由于初制导段导弹动压低,因此使用姿控发动机进行初转弯控制。同时,为了不影响末端复合控制,对姿态修正加上约束条件,即当导弹相对预测命中点的视线偏差角θT≤0.5°、导弹横向角速度|Ω|≤5(°)/s时,停止姿控发动机的修正,初制导结束。
中制导:进行指令修正制导,导弹以30 r/min的速度绕弹体轴自旋。交战控制站(ECS)既跟踪测量目标,又跟踪导弹,每隔一定时间,进行弹道预报,再结合导弹信息,计算预测命中点,将其作为中制导段引导目标点,控制导弹飞向预测命中点,以便实施中、末制导交接班。
末制导:根据PAC-3 Ka波段主动导引头的特性,弹目相对距离小于等于10 km时导弹转入末制导段。此时主动雷达导引头启动,导弹自旋速度提高到180 r/min,弹上计算机自行处理目标数据,控制导弹飞向目标。末制导段按先后顺序分为两个阶段:气动控制段和直接力/气动力复合控制段。导弹在气动控制段实时估算剩余飞行时间tgo,当tgo减至1 s且导引头位于跟踪模式时转入复合控制段。
1.4 自动驾驶仪模型
由于角速度的响应速度远大于气动角,因此应用二时间尺度假设,将系统动态分为快动态和慢动态,快动态为弹体旋转角速度,慢动态为气动角。则导弹自动驾驶仪可分两个回路设计:外回路动态逆控制气动角,生成角速度指令传递给内回路执行;内回路动态逆控制角速度,生成舵偏角指令传递给弹体执行,如图1所示。
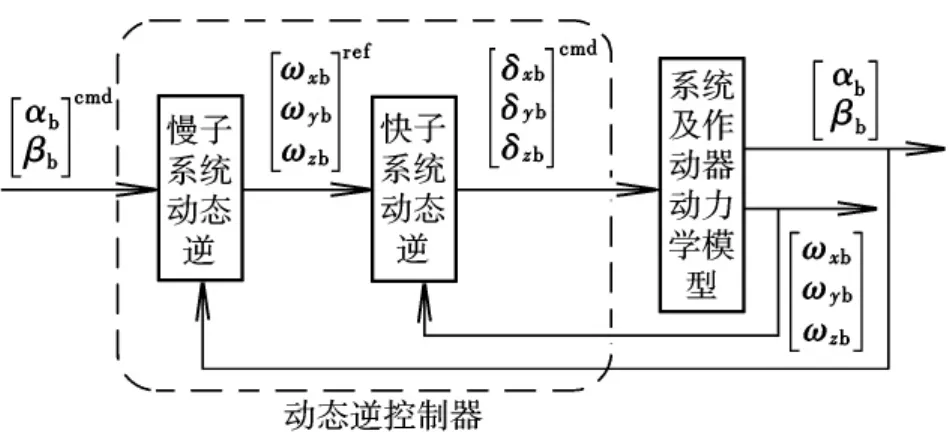
图1 二时间尺度动态逆控制器
首先设计内回路快子系统动态逆,设角速度变化率的期望值为:

式中,ωrefb为角速度参考值;τ1为角速度期望动态的时间常数。由式(1)可得内回路控制律为:
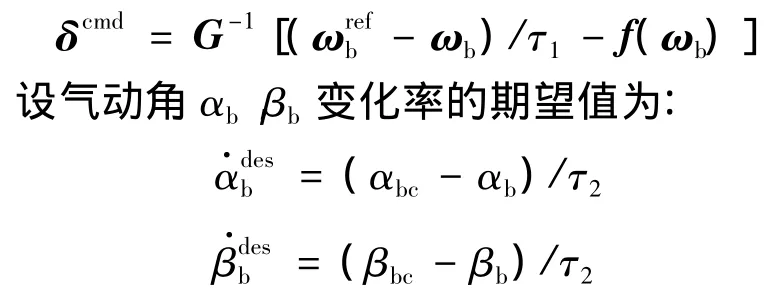
式中,下标c表示指令值;τ2为气动角期望动态的时间常数。由于角速度的响应速度远大于气动角,因此 τ2> τ1,所以设 τ2=kτ1(k 为大于 1 的常数)。由式(2)可得外回路慢子系统控制律为:
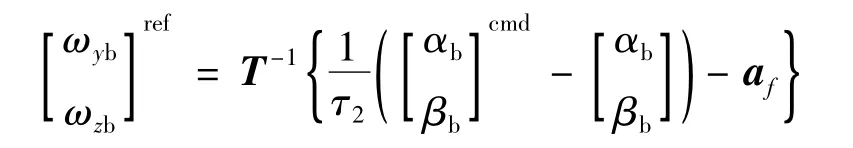
由于导弹在高空或低速情况下动压较小,不能产生需要的控制力矩,所以考虑将所需的控制力矩分配给气动舵和姿控发动机。弹体前端的180个姿控发动机数量有限,所以只在初制导段和末制导段才使用姿控发动机。由于姿控发动机从点火到燃料耗尽过程中推力不可调,因此要保持姿控发动机和气动舵同时工作,形成直接力与气动力的复合控制,如图2所示。

图2 复合控制器结构图
为了使导弹能够快速机动,在复合控制时,先以姿控发动机为主,使其产生与指令力矩接近的力矩,剩下部分再由气动舵执行,这样可以保证舵偏角不达到饱和,且保持其在姿控发动机工作时有一定的调节幅度。图3为复合控制指令分解策略,判断控制力矩是否大于单个姿控发动机产生的力矩,若大于,则启动侧向力;否则,只使用气动控制。
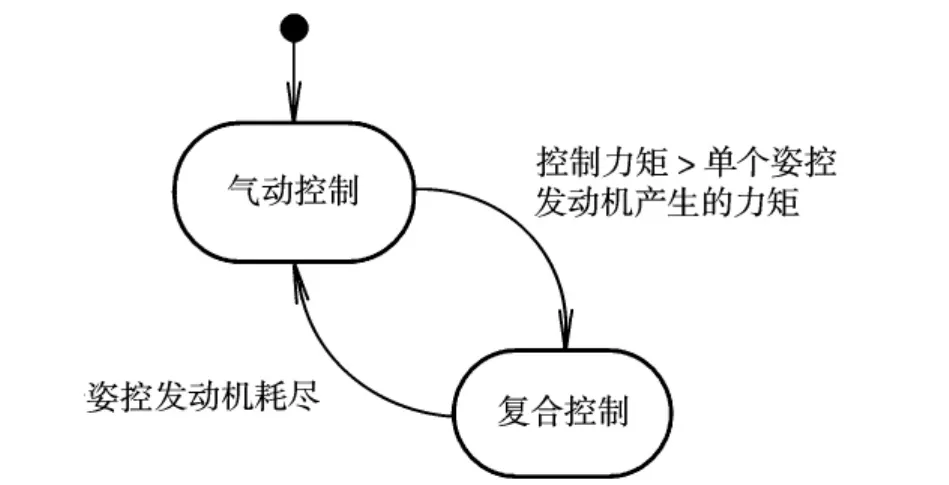
图3 复合控制指令分解策略
2 拦截仿真结果及分析
本文利用VC 6.0软件进行了面向对象的全弹道拦截仿真程序设计。定义PAC-3类,用于拦截弹动力学建模,可声明多个PAC-3对象进行拦截仿真。
在对拦截弹系统建模后,分别对惯性再入TBM目标和拉起下压机动TBM目标进行拦截仿真,分析PAC-3拦截弹拦截弹道导弹的能力。
2.1 多发弹拦截TBM目标算例
导弹初始速度为30 m/s,初始俯仰角为38°,初始气动角为0°;自动驾驶仪慢系统时间常数为0.12 s,快系统时间常数为0.04 s。对惯性再入TBM目标进行拦截仿真。仿真过程中,使用五阶多项式拟合方法进行弹道预报,再利用平均速度法,通过估计剩余飞行时间并利用预报弹道来确定预测命中点。
拦截弹初始位置和发射准备时间tr如表1所示。首先对惯性再入TBM目标进行拦截仿真,目标以50°角再入,落速为1 738.63 m/s。当拦截弹在落点坐标系x轴50 km位置时,地面雷达发现目标,拦截弹准备发射。

表1 拦截弹初始位置和发射准备时间
图4为拦截惯性再入TBM目标三维交战图。图5为3个拦截弹姿控发动机使用情况示意图。姿控发动机呈5行、36列排布,深色区域表示发动机已使用。3个拦截弹的拦截结果如表2所示。

图4 拦截惯性再入TBM目标三维交战图

图5 拦截惯性再入TBM目标姿控发动机消耗示意图

表2 拦截惯性再入TBM结果
2.2 拦截弹可拦截发射点计算
为了得到更全面的拦截仿真结果,调整拦截弹布置点(初始位置),在以保护点(目标落点)为圆心、60 km为半径的圆形区域内,搜索拦截弹对惯性再入目标的可拦截布防区。在拦截仿真结果中,以脱靶量3 m为可拦截标准,剔除了脱靶量大于3 m的情况,将得到的可拦截发射点边界通过支持向量机(SVM)方法进行训练处理,得到拦截弹对不同落角、落速惯性再入目标的可拦截布防区。
图6为目标落速约1 740 m/s时,拦截弹对4种落角目标的可拦截布防区。由图可见,对于相同速度下的惯性再入目标,落角越大,拦截弹的可拦截布防区越大,且布防区在保护点(目标落点)后部范围越大。
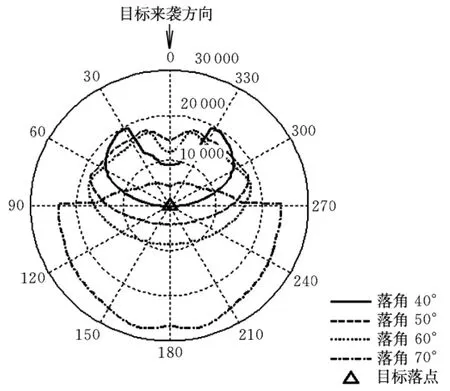
图6 对不同落角惯性再入目标的可拦截布防区
图7为目标落角约50°时,拦截弹对不同落速目标的可拦截布防区。由图可见,在相同落角情况下,不同目标落速对可拦截布防区的大小影响不大;目标落速越大,拦截弹可拦截布防区相对保护点(目标落点)位置越靠前。

图7 对不同落速惯性再入目标的可拦截布防区
3 结束语
本文针对PAC-3拦截弹自旋、复合控制等特点,根据初、中、末制导3个飞行状态,分别设计了不同的导引控制策略。利用VC 6.0软件进行了面向对象的全弹道拦截仿真程序设计,对惯性再入TBM目标进行了多发拦截弹六自由度拦截仿真,并给出了拦截弹对惯性再入目标的可拦截布防区。结果表明,本文建立的拦截弹模型解决了自旋弹的耦合问题,导引控制策略符合PAC-3拦截弹的特性,仿真软件实现了多拦截弹拦截目标的全弹道仿真功能,验证了本文建立的PAC-3拦截弹模型的正确性,该项研究为攻防对抗系统仿真及PAC-3拦截弹性能分析奠定了基础。
[1] 北京航天情报与信息研究所.世界防空反导导弹手册[M].北京:中国宇航出版社,2010:518-522.
[2] O’Reilly P,Walters E.The Patriot PAC-3 missile program—an affordable integration approach [R].ADA319957,1997.
[3] McMillin W C,O’Reilly P.An affordable approach to early cruisemissile defense[R].ADA320130,1996.
[4] 周慧钟,李忠应,王瑾玫.有翼导弹飞行动力学[M].北京:北京航空航天大学出版社,1983:27-47.
[5] 邹晖,陈万春,殷兴良.自旋导弹的反馈线化控制器设计[J].弹箭与制导学报,2004,24(1):228-234.
[6] 邹晖,陈万春,殷兴良.具有侧向脉冲推力的旋转导弹建模与控制研究[J].系统工程与电子技术,2005,27(4):667-691.
[7] 邹晖,陈万春,王鹏,等.敏捷导弹气动力/侧向推力复合控制特性分析研究[J].北京航空航天大学学报,2004,30(3):192-196.
[8] Liu Fang,Chen Wanchun.Controller design for spinning missile with the actuator limit[C]//Wu Fan.Advanced Materials Research Volumes.Switzerland:Trans Tech Publications,2012:45-51.
