紊流风场下的无人机飞行状态卡尔曼滤波估计

周健，王新民，魏宏珅

(西北工业大学自动化学院，陕西西安 710129)

引言

无人机在飞行时会受到各种扰动的影响，其中最重要的影响来自大气紊流［1］。大气紊流的存在会导致飞行速度随机改变，使得测量得到的飞行速度不能直接用于飞行速度控制器的设计。在对象模型确定的情况下，卡尔曼滤波器是针对带有随机噪声信号进行最优滤波的一种有效算法，具有较好的动态和抗干扰性能，能够实现在线状态估计［2-3］。但卡尔曼滤波是在动态噪声和观测噪声均为白噪声的情况下推导出来的［4］，而大气紊流是一种非周期的随机过程，为有色噪声，如果将其当作白噪声处理，势必会影响滤波精度。

本文通过建立符合紊流风场相关特性的有色噪声模型，介绍了一种动态噪声为有色噪声的卡尔曼滤波算法;设计了基于有色噪声的无人机飞行速度卡尔曼滤波器，通过对有色噪声白化处理，构造无人机的状态方程和量测方程，用来估计真实的飞行速度，并给出了相应的计算方法和仿真结果。

1 紊流风场有色噪声建模

在无人机飞行特性仿真分析中，模拟随机风不仅要具有随机性的特征，而且还要符合紊流风场模型的频谱特性和相关特性。紊流风场的模拟原理是将白噪声通过成型滤波器得到符合一定功率谱的有色噪声。为了研究无人机在紊流风扰动中的飞行速度响应特性，需先建立紊流风场模型，本文采用连续大气紊流Dryden模型，其纵向时间频谱函数可表示为［5］:

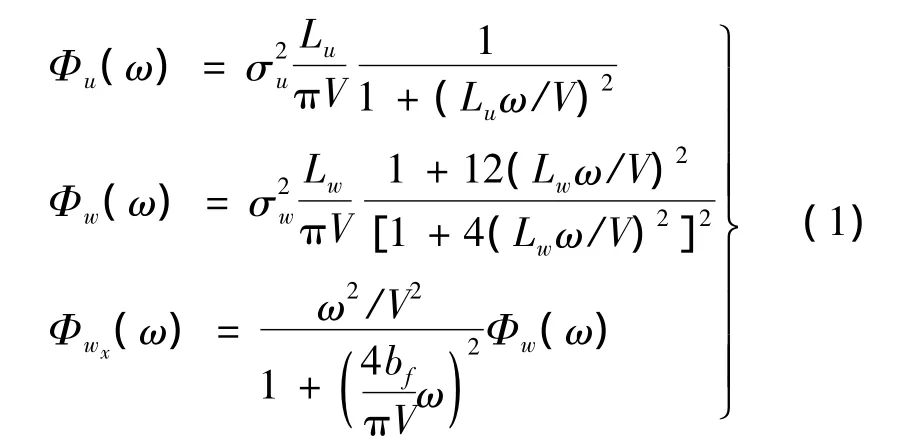
式中，ω 为时间频率;Lu，Lw为紊流尺度;σu，σw为紊流强度;bf为机翼展长;Φu(ω)为紊流轴向速度uw的功率谱密度;Φw(ω)为紊流垂向速度ww的功率谱密度;Φwx(ω)为紊流垂向速度沿飞行方向梯度∂ww/∂x的功率谱密度。

根据线性系统白噪声输入与紊流速度输出的关系，令随机输入r(t)为单位白噪声(即Φrr(ω)=1)，输出频谱为:

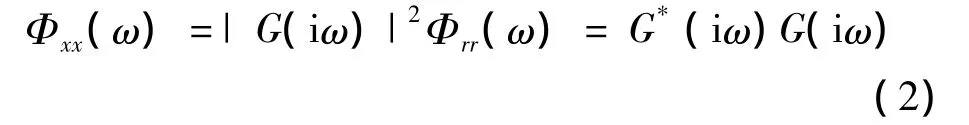
只需将给定的输出频谱Φxx(ω)按式(2)分解就可得到成型滤波器的传递函数G(s)。Dryden模型纵向成型滤波器传递函数G(s)表示如下:

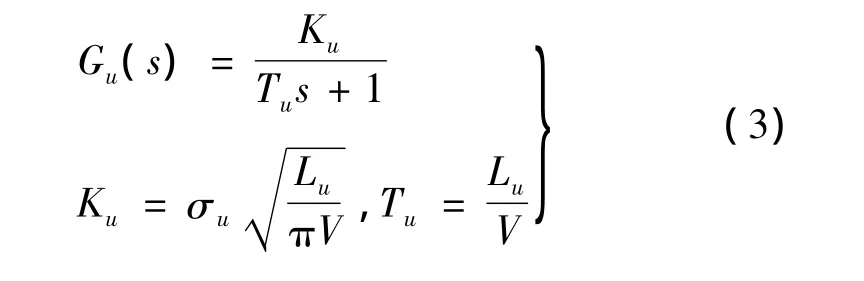
取采样时间间隔为h，对式(6)和式(7)进行离散化，生成的离散序列如式(8)～式(10)所示:

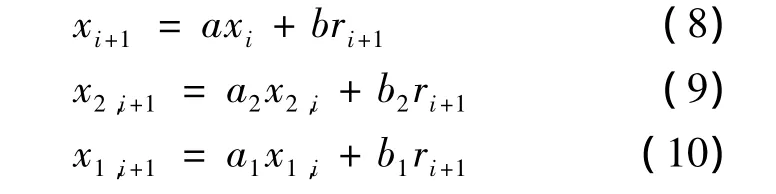
式(9)与式(10)之差就是所需要的紊流信号。其中，ri+1是均值为0、标准差为1的高斯白噪声序列。时间序列各系数求解公式分别为:

2 卡尔曼滤波原理

对于所研究的无人机系统，考虑其离散时间随机状态模型:

式中，Φk，k－1为 tk－1时刻到 tk时刻的一步转移矩阵;Hk为量测矩阵;Γk－1为动态噪声驱动阵;Xk－1为状态向量;Zk为量测向量;εk－1为动态噪声向量;ηk为量测噪声向量。假定系统初态、动态噪声和量测噪声都是均值为零的高斯白噪声。

k－1时刻状态Xk－1的最优线性滤波的递推公式为:

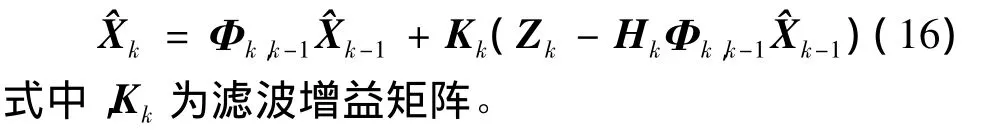
以上的卡尔曼滤波原理是在假定动态噪声和量测噪声为白噪声情况下进行推导的，而实际模型中得到的状态方程和量测方程往往附加着有色噪声。根据理论分析，将紊流风场看作无人机系统的动态噪声，选取动态噪声为有色噪声的卡尔曼滤波器对无人机飞行速度进行估计。量测噪声认为是由速度测量传感器自身引起的，假定为白噪声。

3 有色噪声卡尔曼滤波飞行速度估计

紊流风场时间序列是通过成型滤波器将白噪声转化为有色噪声。在动态噪声是有色噪声的情况下，需要对有色噪声建立数学模型，并将有色噪声白色化，从而就可以使用卡尔曼滤波器对速度状态进行估计［6］。考虑系统噪声为有色噪声而量测噪声为白噪声的无人机，其纵向长周期运动方程为:

式(23)、式(24)符合卡尔曼滤波基本条件。按照卡尔曼滤波方程就可以对无人机飞行速度进行实时估计。

4 仿真验证和分析

以某型无人机为研究对象，将紊流风场加入无人机小扰动方程中，得到紊流风扰动情况下飞行速度响应和理论模型输出的比较结果如图1所示。

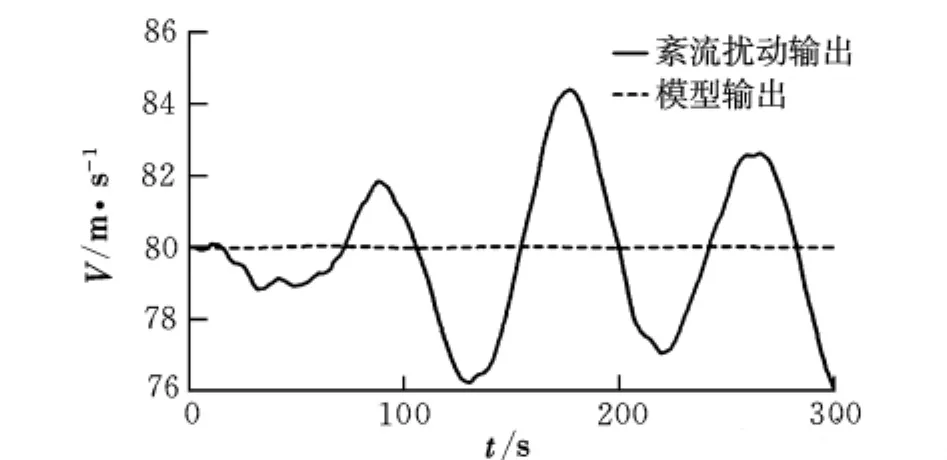
图1 无人机紊流风场下飞行速度响应

从图1中可以看出，无人机飞行速度在紊流风场的影响下有8 m左右的非周期变化，紊流风场对飞行速度的影响较大，无法满足飞行速度控制的输入精度要求。

图2为采用卡尔曼滤波器估计后的飞行速度与紊流风场干扰下的输出结果比较。从图2中可以看出，所设计的滤波器能有效降低紊流风场对飞行速度的影响。

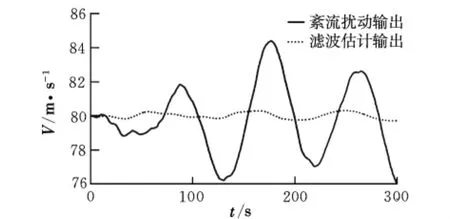
图2 紊流风场下卡尔曼滤波估计的飞行速度

图3给出了滤波估计的飞行速度与实际模型输出的速度残差曲线。

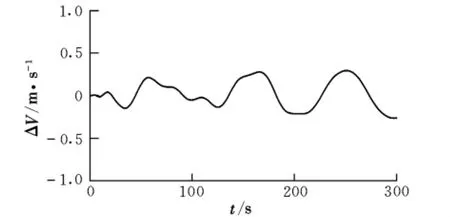
图3 滤波估计输出残差

从图3中可以看出，使用卡尔曼滤波器对飞行速度进行估计具有较小的输出残差，其残差范围在±0.4 m以内，这表明本方法所设计的卡尔曼滤波器能够抑制紊流风对飞行速度的影响，可较准确地估计出紊流风场下真实的飞行速度。

5 结束语

本文针对减小紊流风场对无人机飞行速度影响的问题，通过建立紊流风场有色噪声模型并对其进行数值仿真，验证了所设计的紊流风场模型能够反映真实环境下的风场特性。在模型确定的情况下，设计了动态噪声为有色噪声的卡尔曼滤波器对飞行速度进行估计。研究表明，估计的飞行速度能够较准确地反映真实的飞行速度，能够满足实际飞行中对速度控制的输入精度要求。

［1］ 杨秋艳，王立新.大气紊流环境下的纵向飞行参数响应分析［J］.飞行力学，2009，27(1):20-23.

［2］ 孟凡军，徐国柱.基于卡尔曼滤波器的扰动补偿控制研究［J］.航空科学技术，2010，(3):39-41.

［3］ 赵元峰，唐永哲，赵宝庆.飞机迎角在垂直阵风干扰中的卡尔曼滤波估计［J］.飞行力学，2006，24(3):53-55.

［4］ 崔希璋，於宗俦，陶本藻，等.广义测量平差［M］.北京:测绘出版社，1982.

［5］ 肖业伦，金长江.大气扰动中的飞行原理［M］.北京:国防工业出版社，1993.

［6］ 苏滢滢，蒋心怡，沈斌.有色噪声的实时滤波处理［J］.计算机与数字工程，2008，36(4):143-145.