基于标准特征多项式的横侧向飞控系统设计

2012-03-03吕旸万小朋李爱军徐丽娜

飞行力学 2012年2期

吕旸，万小朋，李爱军，徐丽娜

(1.西北工业大学航空学院，陕西西安 710072;2.西北工业大学自动化学院，陕西西安 710072)

引言

控制律是飞行控制系统设计中的一个非常重要的问题。目前，在飞行控制系统设计的最初阶段，控制律的设计最常用的方法是PID控制方法，但其存在效率低下的缺陷，在很大程度上依赖于设计人员的经验。随着飞行器性能的提高，飞行控制系统也越来越复杂，经典PID控制方法已经成为制约飞行控制系统设计的一个瓶颈。标准特征多项式方法只从数学计算方面进行研究，大大简化了飞行控制系统的设计，是一种标准化的设计方法［1-7］。常见的标准特征多项式有牛顿二项式标准型、Бaттepвopт标准型、ISE准则标准型和ITAE准则标准型等。采用标准特征多项式法，可以使得飞机自动控制系统控制律的设计变得简单化、清晰化。

本文基于标准特征多项式法及其应用的研究成果，对某型飞机横侧向倾斜姿态稳定和航向保持控制进行了标准特征多项式法设计，给出的仿真效果证明了标准特征多项式法对飞机自动控制系统设计的有效性、高效性。

1 基于标准特征多项式的飞控系统设计

本节讨论应用标准特征多项式设计飞行控制系统的方法［2-7］。一般控制系统由控制器和控制对象按负反馈原理建立。设控制器的传递函数为G1(s)，被控对象的传递函数为G2(s)，从而控制系统的闭环传递函数为:

对于4阶、5阶等系统，其控制器设计方法与上述方法相似。

标准特征多项式的参数ω0值的选择具有较大的简便性，如果知道系统的阶次，并给定闭环系统的调节时间ts，由ω0ts=τ就可以确定ω0。但是，如果事先不给出系统的动态性能指标，ω0的选择就有较大的范围，可以根据具体情况而定。

2 倾斜姿态保持/控制模态控制律的设计与仿真

该模态是对飞机的滚转角进行稳定和控制，系统性能要求是:以给定滚转角φg进行盘旋时，精度不低于±1°;其他各参量的曲线平滑，能够快速进入稳定。

以Boeing 707-321飞机滚转角控制系统的控制律设计为例。外回路是滚转角φ反馈回路，内回路是滚转角速率φ·反馈回路。

其控制律的形式为:

巡航速度V0=241 m/s时，飞机数学模型为:

图1为Boeing 707-321飞机基于标准系数法的倾斜姿态保持/控制模态系统框图。

图1 倾斜姿态保持/控制系统框图

选择式(16)和式(17)两个线性无关的方程进行求解，通过变换ω0的值，使求得的两个参数值尽量满足式(15)和式(18)即可。通过计算，选择ω0=2，此时求得的参数值为:Kφ= －54.0504，Kφ·=－64.6652。

仿真中，φg=10°，δa饱和限制在 ±25°。图 2 为Boeing 707-321飞机基于标准系数法的倾斜姿态保持/控制模态的阶跃响应曲线。

由图2可以看出，滚转角曲线能够跟踪滚转角指令信号，并且超调量为0，调节时间为ts=5.26 s，时域响应过渡过程时间和超调量均满足要求，并且能够满足有关飞行品质的要求。

通过计算得到系统的特征多项式为:

图2 倾斜姿态保持/控制模态阶跃响应曲线

3 航向保持/控制回路设计

航向控制回路性能要求是:以给定航向角ψg进行定向飞行时，ψ的精度不低于±1°;其他各参量的曲线平衡，且能快速稳定。

将航向偏差信号同时送入副翼通道和方向舵通道，两个通道的控制律分别为:

副翼控制结构如图3所示。

图3 副翼控制结构框图

飞机航向保持/控制模态控制律结构如上，它以航向角ψ反馈回路为外回路，滚转角φ反馈回路为内回路。

仍然以Boeing 707-321飞机巡航飞行为例，飞机以给定的偏航角进行定航向飞行。

通过计算得到系统的特征多项式为:

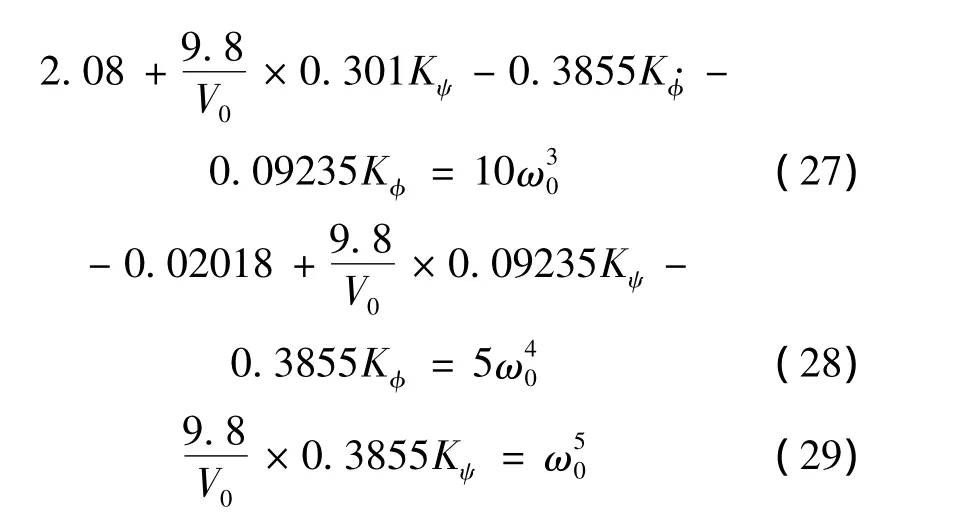
有5个方程、3个待求参数，选择式(26)～式(28)进行求解，通过变换ω0的值，使求得的3个参数值尽量满足式(25)和式(29)即可。由于V0=241 m/s，通过计算，选择 ω0=1.35，此时求得的参数值为:Kψ=169.6836，Kφ·= － 43.1029，Kφ=－41.4799，KH·= －6.1127。

仿真中，ψg=3°，δr饱和限制在 ± 25°。仿真曲线如图4所示。

由图4可以看出，偏航角曲线能够跟踪偏航角指令信号，并且超调量为0，调节时间为ts=6.75 s，时域响应过渡过程时间和超调量均满足要求，并且能够满足有关飞行品质的要求。