多参数控制的全频数字积分器及其稳定性设计

王金鹏，袁 晓

(四川大学电子信息学院，四川成都 610064)

0 引言

微积分运算是一种基本的数学运算，在信号处理领域有广泛的运用［1－2］。数字积分器作为一种重要的器件，在控制，生物工程，雷达等方面有着重要的作用［2－5］。数字积分器在数字电路中是基本的元件，特别是近年数字信号应用的迅速发展，对数字积分器的应用越来越广泛。通过无限脉冲响应(infinite impulse response，IIR)滤波器设计来得到数字积分器的方法目前主要有2种方法:①通过直接推导数值积分的逼近公式来得到数字积分器，如Newton－Cotes规则与Adams－Moulton规则所直接推导出的数字积分器;②将2种性能较好的数字积分器进行线性组合，得到逼近效果好的数字积分器［2－14］。

通过IIR滤波器设计方法设计的数字积分器，传统常使用的数值积分是Newton－Cotes规则，这类积分运算的传输函数满足

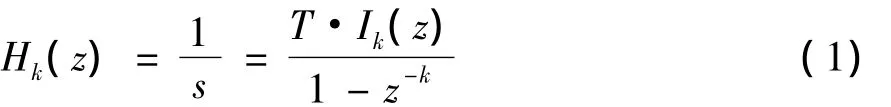
(1)式中:Hk(z)是k阶的Newton－Cotes数值积分器，k是数字积分器的阶数;T是采样周期;Ik(z)是k阶数字积分器的多项式分子。

在Newton－Cotes规则中，数值积分的逼近精度随着阶数 k 的增加而增高［6－9］，但是由 Newton－Cotes规则设计的数字积分器并不完全满足这一规律，因为随着积分函数的阶数k增大，传输函数Hk(z)的极点pi增多，在幅频上会出现很多的冲激，这严重影响着积分器的性能和逼近效果。在设计数字积分器时应当选取适当的阶数k，既要保证新积分器的逼近精度，又要保证其性能。

本文提出一类多参数控制的数字积分器的设计方法，设置参数的选取，得到了幅频精度很高的数字积分器，并进行稳定性分析及稳定性优化。

1 优异的低阶数字积分器

1.1 Al-Alaoui一阶数字积分器

Al－Alaoui考虑将梯形积分器和矩形积分器按照一定的线性规则来构造逼近性能更好的数字积分器，这就是 Al－Alaoui一阶积分器［10－11］。其构造方法如下

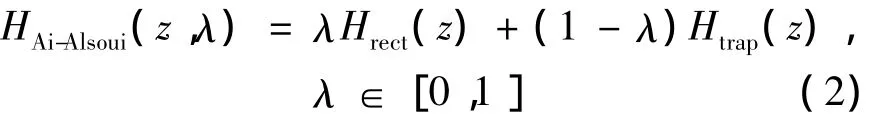
(2)式中:HAi－Alsoui(z，λ)是 Ai－Alsoui的一阶积分器传输函数;Hrect(z)是矩形积分器的传输函数。

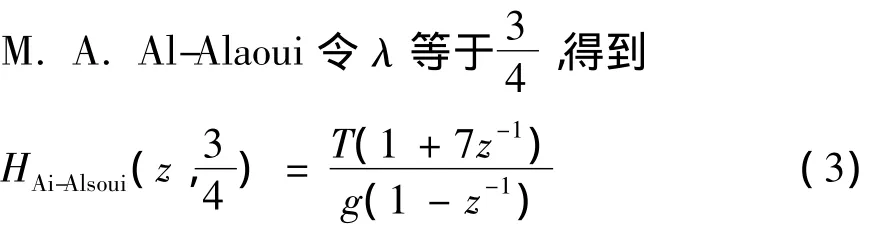
1.2 SKG数字积分器

A.M.Schneider使用 Adams－Moulton 数值积分函数［16，19－20］，得到了一类新的数值积分器［16，20］。得到 的 数 值 积 分 器 叫 SKG(schneider－kaneshigegroutage)积分器，该积分器的传输函数为

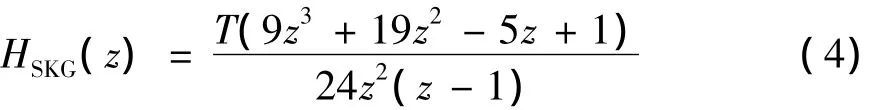
(4)式中:HSKG(z)是SKG积分器的传输函数。

1.3 Gupta宽频数字积分器

Maneesha Gupta也是利用Al－Alaoui的线性组合方法构造出了宽频数字积分器［15］，如(5)式，该积分器是由梯形积分器和SKG积分器的线性组合构造而成。

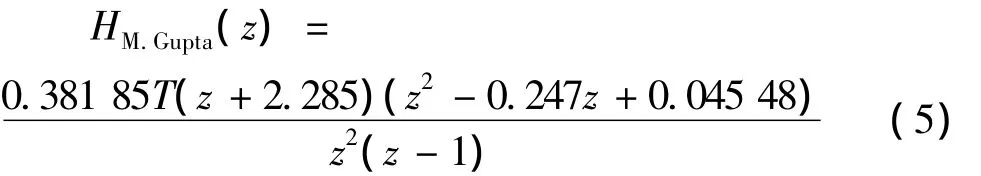
(5)式中:HM.Gupta(z)是Gupta宽频数字积分器的传输函数。

这3类数值积分器的精度都是比较高的，如图1所示，对y轴取对数后，可以得到:Al－Alaoui积分器在低频和中频效果比较好，但是在高频部分效果很差;SKG数值积分器在低频和高频部分逼近效果好，但是在中频部分效果比较差;M.Gupta宽频数值积分器在整个频带内逼近效果都比较好。

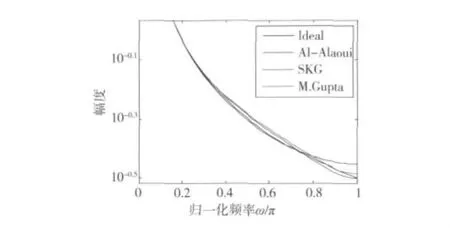
图 1 T=1，Al－Alaoui，SKG 和 M.Gupta 宽频积分器和理想积分器的幅频图Fig.1 Magnitude responses of the ideal，Al－ Alaoui，SKG and M.Gupta wideband integrator

2 新的数字积分器设计与性能分析

2.1 多控制参数的数字积分器

目前，比较精确的积分器有Gupta宽频积分器和Al－Alaoui一阶积分器，都是利用2种数字积分器的线性组合来构造新的数字积分器。

我们定义一个线性组合基本公式为

(7)式中:HNew(z，λ1，λ2，λ3)是该类数字积分器的传输函数;λ1，λ2，λ3∈［0，1］。选择不同的 λ1，λ2，λ3参数值，可以得到一类数目众多的数字积分器。

2.2 控制参数的选取

要得到在整个频带内逼近效果好的数字积分器，控制参数的选取应该满足一定的原则。(8)式中:ε(ω)是绝对幅度误差函数;Hid(ejω)是理想积分器的传输函数。

定义积分器的绝对幅度误差面积［15］为

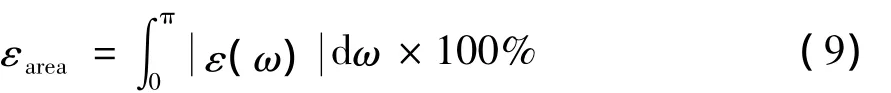
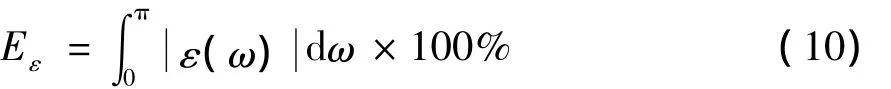
(10)式中，Eε是积分器的绝对幅度误差能量。

全频数字积分器的控制参数选取原则:选取适当的 λ1，λ2，λ3，使 εarea小于 1，Eε在 10－4数量级之下，并且要让ε(ω)在整个频带内控制在0.02以内(Al－Alaoui一阶积分器的低频部分和M.Gupta宽频数值积分器的高频部分都能保证的误差如图2所示)。这样就可以得到全频带的数字积分器。

按照上面的原则设计数字积分器，通过实验不断改变3个参数λ1，λ2，λ3的值，得到一组使数字积分器逼近效果好的参数:λ1=0.97，λ2=0.29，λ3=0.7。

将这3个参数代入(7)式中，得到该新数字积分器的传输函数为

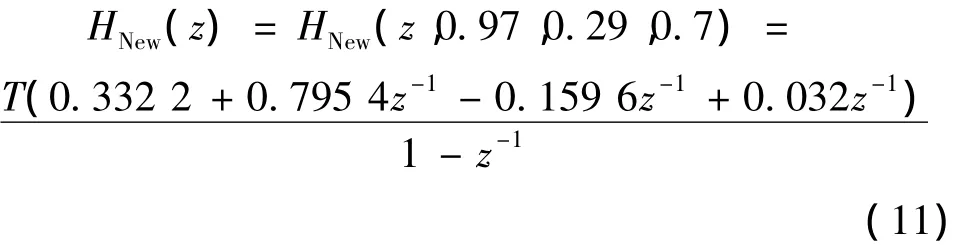
(9)式中，εarea是积分器的绝对幅度误差面积。

定义积分器的绝对幅度误差能量［12］为

(11)式中，HNew(z)即所设计的全频数字积分器。

2.3 性能分析

对新设计的数字积分器进行误差分析，主要是对于该积分器对理想积分器的绝对幅度误差ε(ω)、绝对幅度误差面积εarea和绝对幅度误差能量进行分析。

Al－Alaoui一阶数字积分器，M.Gupta 宽频数字积分器，SKG积分器和新构造的数字积分器的绝对幅度误差曲线如图2所示。可以看出，Al－Alaoui一阶积分器在高频部分(0.8πω≤π)逼近效果很差;SKG数值积分器在中频部分(0.3πω≤0.8π)效果比较差;M.Gupta宽频数值积分器在整个频带内逼近效果较好，且当0≤ω≤π时，绝对幅度误差εM.Gupts(ω)小于0. 03;而新设计的数字积分器当0≤ω≤π 时，有 εNew(ω)0.015，在整个频带内比 Al－Alaoui一阶数字积分器、M.Gupta宽频数字积分器和SKG数字积分器逼近效果更好。

这些积分器对理想积分器的绝对幅度误差面积εares和绝对幅度误差能量Eε如表1所示。可以很明确地知道，新设计的积分器的绝对幅度误差和绝对幅度误差能量在一个频率周期内比Maneesha Gupta宽频数字积分器、SKG数字积分器和Al－Alaoui一阶积分器小了一个数量级。由此可知，新设计的数字积分器有更小的误差，更加逼近理想积分器，拥有很高的幅频精度。

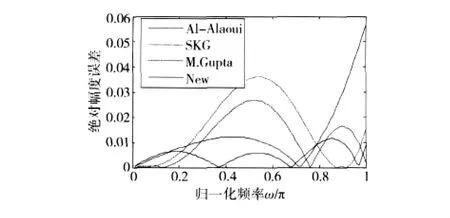
图2 T=1时，4种数字积分器的绝对幅度误差图Fig.2 Absolutemagnitude errors of the four types integrator with T=1

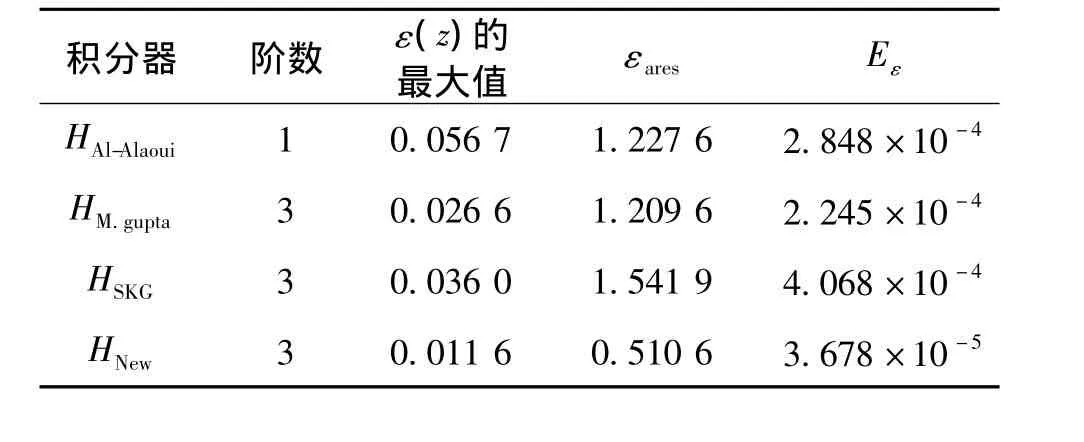
表1 T=1时，4种数字积分器的最大绝对幅度误差值、绝对幅度误差面积和绝对幅度误差能量比较Tab.1 Maximum absolutemagnitude errors，the absolutemagnitude errors area and energe of the four types integrator with T=1

3 数字积分器的稳定性分析

根据Al－Alaoui提出的积分器稳定性设计方法［12，18］，进行稳定性的设计。

①得到积分器的传输函数1/s。数字积分器本身就是对模拟积分器的逼近，由新积分器的传输函数如(11)式，根据积分器的性质可以得到

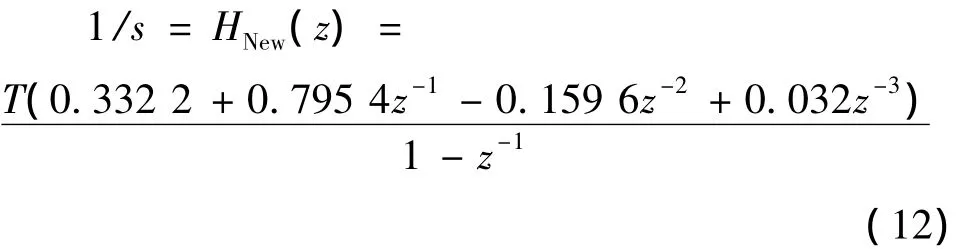
(12)式中:1/s是理想积分器的传输函数。

②转化为s的函数，将其描述为 s－to－z的方式，那么

(15)式中:数字积分器就是设计的稳定数字积分器。图3为T=3，全频数字积分器，稳定性设计后的数字积分器及理想数字积分器的幅频图，对y轴取对数，可以清晰的看到，稳定性处理后的数字积分器的逼近性能有所减低。

4 结束语

利用各数值积分器的线性组合构造新的积分器，该积分器在幅频上更加逼近理想积分器，在整个频带内都有很好的逼近效果。这就使得在工程上运用新的数字积分器可以得到更加精确的积分运算，同时，这种线性构造积分器的方法也能扩展构造数字积分器的方法。然后对该积分器进行了稳定性分析，进行了稳定性的优化。

数字积分器的发展迅速，但是仍然面临很多挑战，如何同时增强数字积分器的逼近性和稳定性，高性能的分数阶积分数字积分器设计，分数阶积分的数字积分器性能判断，数字控制系统分析理论如何渗入数字积分器设计之中等，在信息科学中，这一研究方向一定会出现良好的前景和丰硕的成果。

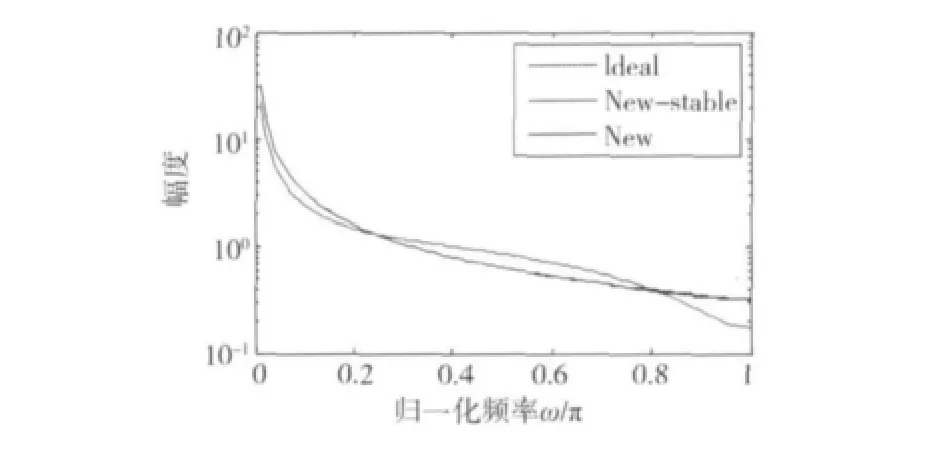
图3 T=1时，全频数字积分器，稳定性设计后的数字积分器，及理想数字积分器的幅频图Fig.3 Magnitude of the ideal integrator，unstable and stable full spectrum band integrator whit T=1

［1］袁晓，张红雨，余厥邦.分数导数与数字微分器设计［J］.电子学报，2004，32(10):1658－1665.

YUAN Xiao，ZHANG Hong－yu，YU Jue－bang.Fractional－Order Derivative and Design of Fractional Digital Differentiators［J］.Acta Electronica Sinica，2004，32(10):1658－1665.

［2］TSENG C C.Digital Integrator Design Using Recursive Romberg Integration Rule and Fractional Sample Delay［C］//Circuits and Systems，2007.ISCAS 2007.IEEE International Symposium，New Orleans:IEEE Press.2007:2726－2729.

［3］TSENG CC.Digital IIR Integrator Design Using Richardson Extrapolation and Fractional Delay［J］.IEEE Transactions on circuits and systems－I:Regular Papers.2008，55(8):2300－2309.

［4］TSENG Chien－cheng，LEE Su－ling.Design of digital IIR Integrator Using Discrete Hartley Transform Interpolation Method［C］//Circuits and Systems，2009.ISCAS 2009.IEEE International Symposium on，Taipei:IEEE Press，2009:2181－2184.

［5］TSENG Chien－cheng.Closed－Form Design of Digital IIR Integrators Using Numerical Integration Rules and Fractional Sample Delays［J］.IEEE Transactions on circuits and systems－ I:Regular Papers.2007，54(3):643－655.

［6］WILLIAM H P，SAUL A T，WILLIAM T V，et al.Flannery.Numerical Recipes－The Art of Scientific Computing，3nd ed［M］.New York:Cambridge University Press，2007.

［7］ENDRE S，DAVID F M.An Introduction to Numerical Analysis［M］.New York:Cambridge University Press，2003.

［8］STEVEN T K.Numerical Analysis Using MATLAB and Spreadsheets Second Edition［M］.Orchard Publications.2004.

［9］AL－ALOUIM A.Novel Class of Digital Integrators and Differentiators［J］.IEEE transactions on Signal Processing.2009，pp(99):1－1.

［10］AL－ALOUIM A.Al－Alaoui operator and the new transformation polynomials for discretization of analogue systems［J］.Electrical Engineering，2008，90(6):455－467.

［11］AL－ALOUIM A.Al－Alaoui operator and the α－approximation for descretization of analog systems［J］.Facta Univ.Electrical Engineering，2006，19(1):143－146.

［12］M.A.Al－Alaoui.Class of digital integrators and differentiators［J］.IET Signal Process，2011，5(2):251－260.

［13］AL－ALOUIM A.Using fractional delay to control the magnitudes and phases of integrators and differentiators［J］.IET Signal Process，2007，1(2):107－119.

［14］AL－ALOUI M A.Novel approach to analog to digital transforms［J］.IEEE Trans.Circuits Syst.I，Fundam.Theory App.，2007，54(2):338－350.

［15］GUPTA M，JAIN M，KUMAR B.Wideband Digital Integrator［C］//Multimedia，Signal Processing and Communication Technologies，2009.IMPACT 2009.International，Aligarh:IEEE Press，2009:106－108.

［16］ALAN M S，KANESHIGE JT，GROUTAGE FD.Higher Order s－to－z Mapping Functions and Their Application in Digitizing Continuous－Time Filters［J］.Proceedings of the IEEE，1991，79(11):1661－1674

［17］NAM Q N.A New Approach for the Design ofWideband Digital Integrator and Differentiator［J］，Circuits and Systems II，2006，53(9):936－940，2006.

［18］AL－ALOUIM A.Novel Stable Higher Order s－to－z Transforms［J］.IEEE Transaction on circuits and systems－I:Fundam.Theory App.，2001，48(11):1326－1329.

［19］杨大地，郑兴武.一类特殊的Adams—Moulton公式［J］.重庆工学院学报:自然科学版:2007，21(10)，10－17.

YANF Da－di，ZHENG Xing－wu.Class of Special Adams－Moulton Formulas［J］.Journal of Chongqing Institute of Technology:Natural Science Edition:2007，21(10)，10－17.

［20］ALAN M S，JAMESA A，IHAB SB.Accuracy and Stability of Discrete－Time Filters Generated by Higher－Order s－to－z Mapping Functions［J］.IEEE Transactions on Automatic Control.1994，39(2):435－441.

(编辑:刘 勇)