光学非球面超精密磨削的微振动对成形精度影响研究

张学忱，曹国华，聂风明，吴庆堂

(1.长春理工大学 机电工程学院，吉林 长春130022;2.长春设备工艺研究所，吉林 长春130022)

0 引言

随着现代空间技术的发展和光学系统成像质量要求的不断提高，非球面光学系统设计与制造技术越来越得到国内外研究者和企业的重视。目前高精度大中口径非球面超精密磨削加工技术成为国内外研究的重点领域，非球面超精密磨削加工的面型精度直接关系到研抛的效率和非球面的光学质量。超精密磨削是多种因素综合作用的微米级加工技术，加工过程中产生的微振动，使工件表面形成微振动波纹和形状误差，会严重影响加工的面型精度，并加剧砂轮的磨损，降低磨削效率［1-2］。近年来国内外研究者开展了解决或降低微振动的研究，试图找出各种因素与加工过程中微振动的关系和补偿技术来提高磨削精度［3-4］。Li 等［5］建立了脆性光学材料轮廓磨削加工的振动模型，研究了磨削刚度与振动的关系;张翊等［6］建立了轴对称非球面磨削中砂轮与工件加工时的振动数学模型，估计了砂轮振动频率和幅值变化和工件主轴频率及加工进给速度变化对工件表面质量的影响趋势。杨小璠等［7］分析了超精密磨削时砂轮振动和工件主轴振动产生的原因及对工件表面质量产生的影响，在数控车床刀架上设计了一套微小振动试验系统，通过激振器使3 个方向产生模拟精密磨床上砂轮X 轴、Z 轴和Y 轴的微小振动，分析了系统各向微振动叠加后总的位移响应和位移响应误差。本文通过分析非球面磨削时砂轮轴和磨床主轴微振动对加工精度的影响，建立了砂轮轴和磨床主轴的径向振动和轴向振动对磨削非球面面型精度影响的数学模型，提出了微振动位移动态测量方法，对砂轮轴转速、主轴转速、砂轮轴和磨床主轴静压轴承油压的选择，确定磨削工艺参数，降低表面波纹度。

1 微振动对成形精度影响分析

轴对称非球面光学元件超精密磨削加工过程中，由于轴及轴上零件材质分布不均、制造和安装误差等因素的影响，磨床砂轮轴和主轴的不平衡量使砂轮轴和主轴产生弯曲振动﹑扭转振动﹑纵向振动，引起磨削砂轮和装夹在主轴上的被磨非球面元件的径向和轴向微位移，从而影响磨削成形精度和表面波纹度。设支撑砂轮轴和主轴的液体静压轴承的径向刚度无限大，把砂轮轴和主轴的不平衡质量等效到安装砂轮和工件的轴端，则砂轮轴、主轴的径向微振动位移为

式中:e 为质心与轴向的偏心距;ω 为轴的角速度;k为轴的弯曲刚度。

图1为大中口径非球面超精密磨床的砂轮轴和主轴的微振动引起的磨削表面轮廓的原理简图。采用包络法磨削加工非球面，首先是粗磨，将毛坯磨成一个比较接近要求的面形，然后精磨。非球面光学元件磨削加工中砂轮轴在X、Y 方向上按二次曲线方程移动和旋转，非球面元件的主轴装夹平面绕Y坐标旋转，由于砂轮侧母线是直线或是圆弧曲线，为保证砂轮磨削点不变，装载砂轮的转台必须与X、Y联动，保证砂轮磨削点k 与非球面面型相切，进行高速磨削加工得到非球面。设磨削点k 在x1o1y1中砂轮轴o1x1与主轴径向OX 的夹角为α，砂轮半径方向o1y1与OX 夹角为β，设砂轮径向微振动位移为a1，轴向微振动位移为b1.非球面磨削过程中砂轮径向和轴向微振动位移在XOY 坐标系中引起的径向偏差rx和轴向偏差ry如(2)式及非球面的球面半径偏差Δr1如(3)式。

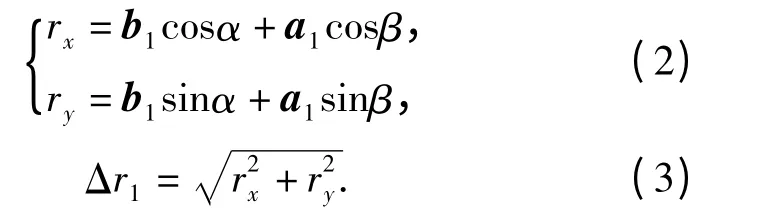
同理，在XOY 坐标系中设磨床主轴轴向微振动位移为a2，径向微振动位移为b2，磨床主轴微振动引起的非球面球面半径偏差Δr2如下式:

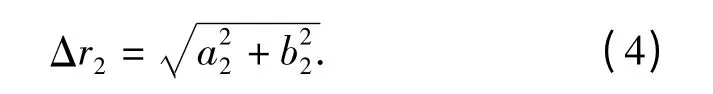
由砂轮轴和磨床主轴微振动引起的非球面球面综合偏差Δr 如下式:

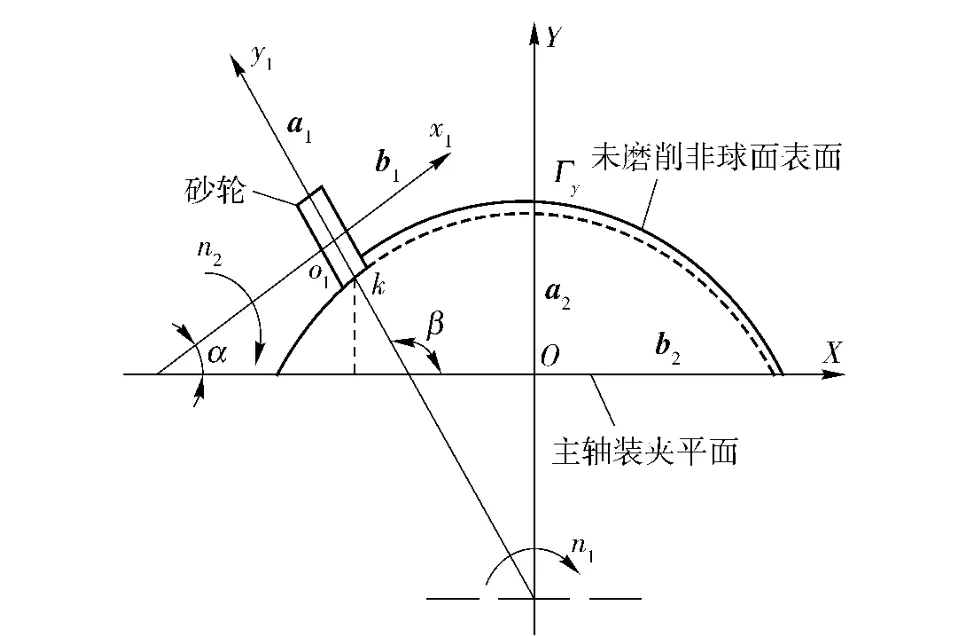
图1 砂轮轴和主轴的微振动引起表面轮廓精度的原理图Fig.1 Diagram of the surface profile precision caused by grinding wheel and spindle micro-vibration

2 微振动位移测量原理及装置

激光测量技术可非接触精确测量被测物体的位置、位移等变化，主要应用于检测物体的位移、厚度、振动、距离、直径等几何量的测量［8-9］。激光位移测量技术按测量原理分为激光三角测量法和激光回波分析法，激光三角测量法具有非接触、测量点小、分辨率高、结构简单、可用于实时在线快速测量的优点，一般适用于高精度、短距离的测量，而激光回波分析法则用于远距离测量。本文采用激光三角法测量砂轮轴和主轴的微振动，其测量原理如图2所示，半导体激光器LD 发出的激光经透镜L1 聚焦，使激光光斑垂直照射到被测轴表面而形成物光点，轴表面形成的反射和散射激光经接收透镜L2 会聚到CCD 原件上而形成像光点。一般采用发射光轴与被测表面重复的入射方式，当被测物体与三角法测头之间发生相对位移时，其轴上的物光点沿入射方向发生位移X，并引起像光点在CCD 上发生位移X'，使CCD 输出信号变化，通过检测CCD 输出信号的变化被测轴的微振动位移如下式:

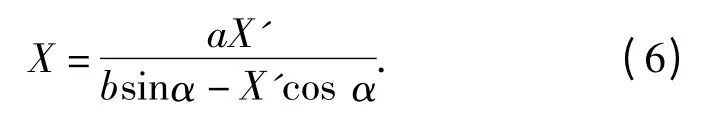
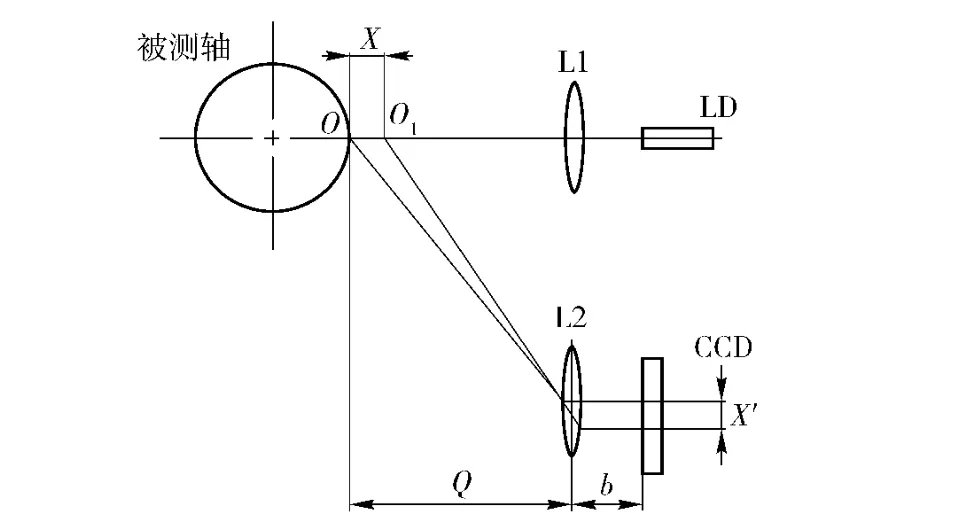
图2 激光三角位移测量原理Fig.2 Laser triangulation measurement principle diagram

微振动位移的动态测量装置由高精度ZS -HLDS2 激光位移传感器和传感器固定支架、磁力表座和测量分析软件组成。测量范围为±1 mm，激光光斑大小为1 mm×20 μm，分辨率为0.02 μm，测量精度为± 0.1 μm，采样周期为110 μs、500 μs、2.2 ms、4.4 ms.利用微振动位移动态测量装置在所研制的大中口径非球面超精密磨削机床上进行了砂轮轴和主轴的微振动测量。该磨床可磨削平面、球面、非球面等元件，加工直径可达0.5 m;机床采用大理石床身，磨床主轴和砂轮轴采用液体静压轴承支撑，液体静压轴承的静压支撑刚度为1 800 N/μm.经静态测量砂轮轴的径向误差小于0.075 μm，轴向误差小于0.05 μm，磨床主轴的径向误差小于0.078 μm，轴向误差小于0.051 μm，转台的回转精度小于0.05 μm，砂轮回转精度低于1 μm，图3为砂轮轴微振动位移测试安装方式。

图3 砂轮轴微振动位移测试安装方式Fig.3 The installation method of wheel axis micro-vibration displacement test

3 主轴和砂轮轴微振动位移结果分析

超精密非球面磨削机床的主轴和砂轮轴采用液体静压轴承支撑，液体静压轴承的油压决定其支撑刚度，而油压和轴的转速匹配是否合适直接影响微振动位移。本文利用图3所示微振动位移动态测量装置测得砂轮轴在油压为0.8、1.1、1.3 MPa 时，转速为800、900、1 000、1 100、1 200、1 300、1 400、1 500 r/min 时的径向微振动位移如图4所示，轴向微振动位移如图5所示。可见随着砂轮轴转速的增加，砂轮轴径向和轴向微振动位移降低，转速从800 r/min 变化到1 500 r/min 时，保持液体静压轴承油压不变，径向振动变化在1.5 μm 以内，轴向振动变化在0.2 μm 以内;当砂轮轴转速为1 400 r/min时，液体静压轴承油压在0.8 MPa 时，砂轮的轴向和径向振动都达到最小值。

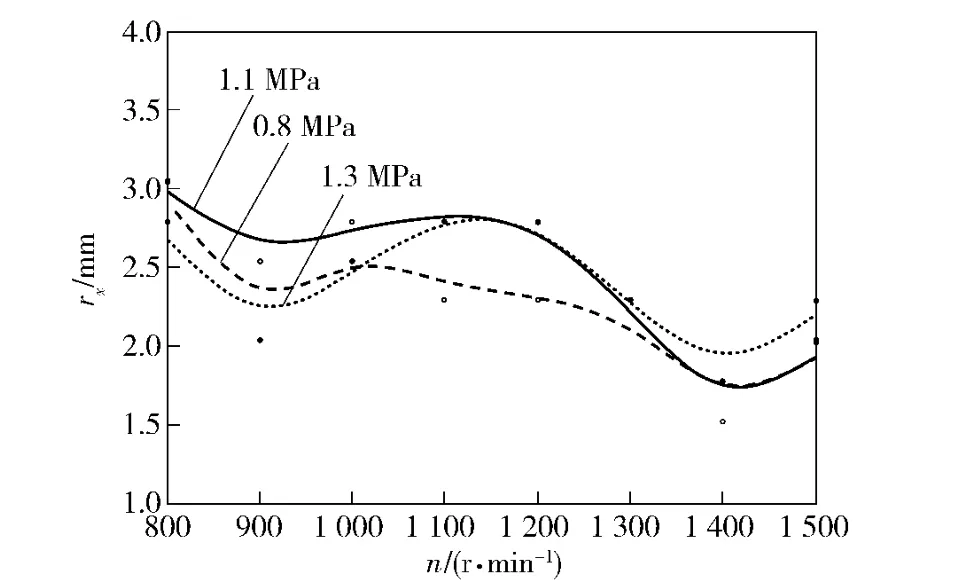
图4 砂轮轴径向振动幅值Fig.4 The radial vibration amplitude of wheel shaft

磨床主轴轴向安装有装夹被磨削非球面光学元件的装夹平面，该平面为刮研面，且主轴轴向微振动位移很小。因此本文测得主轴在油压0.8、1.1、1.3 MPa 时，转速分别为50、60、70、80、90、100、110、120 r/min 时的径向微振动位移如图6所示。可见随着主轴转速的增加，主轴径向微振动位移降低，转速从50 r/min 变化到120 r/min 时，保持液体静压轴承油压不变，径向振动变化在1 μm 以内;当主轴转速为100 r/min 时，液体静压轴承油压在1.1 MPa时，主轴的径向振动达到最小值。

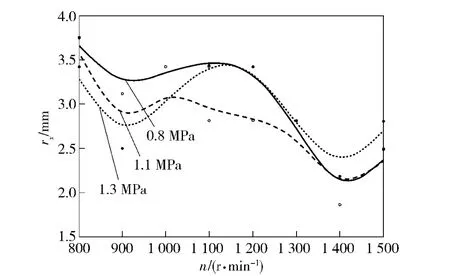
图5 砂轮轴轴向振动幅值Fig.5 The axial vibration amplitude of wheel spindle

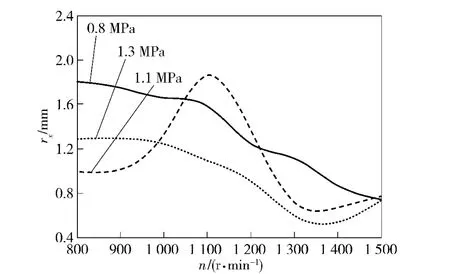
图6 磨床主轴径向振动幅值Fig.6 The radial vibration amplitude of grinder spindle

4 结论

本文系统研究了非球面超精密磨削过程中砂轮轴和磨床主轴微振动对加工精度的影响，建立了砂轮轴和磨床主轴的径向微振动和轴向微振动对磨削非球面面型精度影响的数学模型，并分析了砂轮轴和磨床主轴转速、砂轮轴静压轴承和磨床主轴静压轴承油压对砂轮轴和磨床主轴的径向微振动的影响，给出了该磨床磨削非球面的合理工艺参数为:主轴100 r/min，油压1.1 MPa;砂轮轴1 400 r/min，油压1.1 MPa.提出的主轴和砂轮轴的微振动位移动态测量方法，对合理选择砂轮轴和主轴转速及砂轮轴和磨床主轴静压轴承油压，合理确定磨削工艺参数，提高磨削成形精度具有学术和工程应用价值。

References)

［1］ 杨福兴.大口径平面光学元件超精密加工技术的研究［J］.光学技术，2004，1:27 -29.YANG Fu-xing.Large diameter plane optical element ultra-precision processing technology［J］.Optical Technique，2004，1:27 -29.(in Chinese)

［2］ Huang H，Guo Y B.Research on aspheric machining system error compensation and experiment eliminate the error wave area［J］.International Journal of Computer Applications Technology，2007，29(7):150 -154.

［3］ Zhan Jian-ming，Yu Si-hai.Study on error compensation of machining force in aspheric surfaces polishing by profile-adaptive hybrid movement-force control［J］.International Journal of Advanced Manufacturing Technology，2011，54:879 -885.

［4］ Sazedur Rahman M，Saleh T，Lim H S，et al.Development of an on-machine profile measurement system in ELID grinding for machining aspheric surface with software compensation［J］.International Journal of Machine Tools ＆ Manufacture，2008，48:887 -895.

［5］ Li Y，Gracewski S M，Funkenbusch P D，et al.Analysis of chatter in contour grinding of optical materials［J］.International Journal of Machine Tools ＆ Manufacture，2002，42:1095 -1103.

［6］ 张翊，郭隐彪，庄司克雄.微小振动影响超精密非球面加工精度的研究［J］.金刚石与磨料磨具工程，2003，(3):17-20.ZHANG Yi，GUO Yin-biao，Syoji Katsuo.Influence of chatter vibration on the ultra precision machining accuracy of aspheric surface［J］.Diamond and Abrasives Engineering，2003，(3):17 -20.(in Chinese)

［7］ 杨小璠，郑琳，郭隐彪.超精密磨削加工微小振动模拟系统研究［J］.组合机床与自动化加工技术，2004，(6):17 -20.YANG Xiao-fan，ZHENG Lin，GUO Yin-biao.Ultra-precision grinding machining small vibration simulation system research［J］.Modular Machine Tool ＆ Automatic Manufacturing Technique，2004，(6):17 -20.(in Chinese)

［8］ 吴剑锋，王文，陈子辰.激光三角法测量误差分析与精度提高研究［J］.机电工程，2003，5:89 -91.WU Jian-feng，WANG Wen，CHEN Zi-chen.Laser triangulation measurement error analysis and the accuracy enhance［J］.Journal of Mechanical and Electrical Engineering，2003，5:89 -91.(in Chinese)

［9］ Usanov D A，Skripal A V.Quantum Electronics Measurement of micro-and nanovibrations and displacements using semiconductor laser autodynes［J］.Quantum Electronics，2011，41(1):86-94.