车载微光瞄准镜电子稳像技术研究

宗艳桃，蒋晓瑜，汪熙，纪红霞，赵锴

(1.装甲兵工程学院 控制工程系，北京100072;2.61135 部队，北京102211)

0 引言

“下反”稳像火控系统利用陀螺仪的定轴性直接稳定瞄准镜主光路下部的反射棱镜，实现了视场在方位向和高低向的稳定，具有结构简单、经济性较好等优点。但是，当“下反”稳像火控系统嵌入微光夜视功能时，新的光路难以通过反射棱镜，车体行进时微光图像会随着火炮振动在瞄准分化周围晃动［1-2］。

电子稳像(EIS)是指利用稳像算法对图像的抖动进行补偿，获得视觉上稳定的图像序列的技术，其实现流程如图1所示。运动矢量估计对电子稳像的精度和速度影响最大［3-6］，主要有两种方法:一种是利用运动估计算法从图像中提取;另一种是利用传感器直接测量。前者需要占用较长的计算时间，尤其当图像抖动剧烈或存在运动目标等复杂情况时，电子稳像的实时性和准确性受到很大影响;后者实时性强，但稳像精度受限于传感器精度和模型误差。

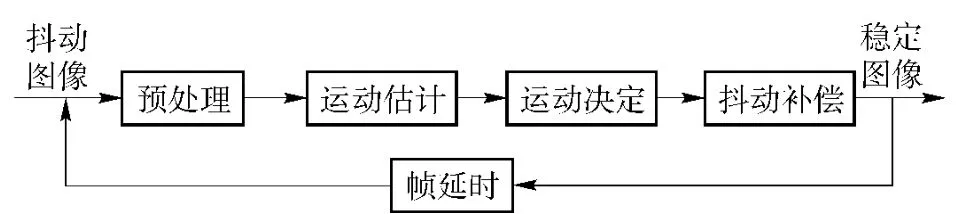
图1 电子稳像实现流程Fig.1 Electronic image stabilization implementation procedure

“下反”稳像火控系统安装了两自由度陀螺仪，因此在其基础上增加了块匹配电子稳像算法，来实现对微光图像的快速高精度稳定，提高乘员夜间观察瞄准目标的能力。

1 电子稳像系统总体设计

电子稳像系统主要由微光瞄准镜视频采集模块、陀螺仪信号采集模块、DSP 电子稳像模块、视频显示模块4 部分组成，其总体结构如图2所示。

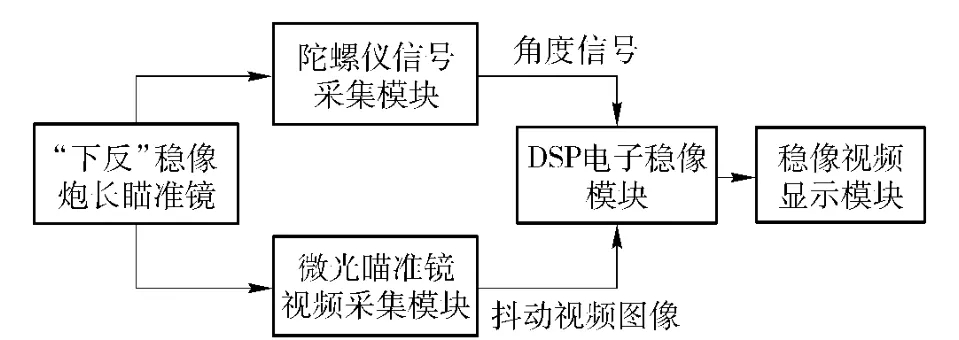
图2 微光稳像系统的总体结构Fig.2 Low-light-level image stabilization system overall structure

电子稳像直接对视频图像进行处理，因此首先需要对微光瞄准镜作必要的改造，利用视频采集模块获取微光图像，将其转化为数字视频信号。视频采集模块直接安装在微光瞄准镜的护眼圈螺纹上，摄像机的入瞳与瞄准镜的出瞳一致保证了图像质量，同时联接牢靠，且便于降级使用。稳像后的视频图像通过视频显示模块输出，乘员直接观察液晶屏，更加方便轻松。为便于安装，将陀螺仪信号采集模块、DSP 电子稳像模块、视频显示模块集成在稳像器盒中，结构紧凑，可以直接安装在瞄准镜支架上。

陀螺仪在工作过程中，由于自身机械结构摩擦不平衡力矩等因素的影响，难以避免的存在随机抖动，对长焦距成像系统产生较大影响;同时还存在车辆水平振动的影响以及图像运动模型误差。这些误差都会造成微光图像在经过补偿后仍存在一定抖动，需要进一步采用稳像算法对图像进行稳定。

稳像系统工作流程如下:

1)陀螺仪信号采集模块将信号传递给DSP 电子稳像模块，转换为图像运动矢量的初始估计值。

2)块匹配算法在其基础上对当前图像和参考图像进行搜索匹配，获得运动矢量的精确值。

3)然后电子稳像程序根据图像运动模型，对图像的抖动进行补偿，稳定后的微光图像通过视频显示模块输出给炮手。

2 基于陀螺仪的运动矢量初始估计

在炮长微光瞄准镜中的图像进行稳像补偿之前，首先需要分析瞄准镜运动和图像运动的对应关系，进而确定合适的图像变换模型以及陀螺仪角度信号与图像运动矢量的比例系数。

2.1 陀螺仪估计运动矢量模型分析

在三维计算机图形学的研究中，摄像机成像应采用透镜成像模型，几何关系称为透视投影.为了简化问题的处理同时又满足应用的需要，常用小孔成像模型来代替透镜成像模型［7］。

在图3中，OXYZ 表示摄像机坐标系，oxy 表示摄像机成像面坐标系，摄像机视轴指向Z 轴方向。设世界坐标系内的一个景物点P 的坐标为(X1，Y1，Z1)，其投影在成像面上的像点p 的坐标为(x1，y1)，f 为摄像机的焦距。根据小孔成像原理，像点与景物点坐标有如下近似关系式:

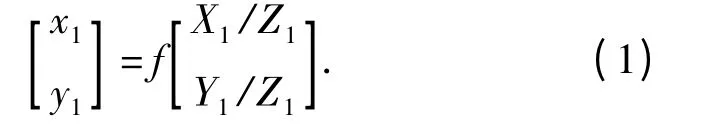
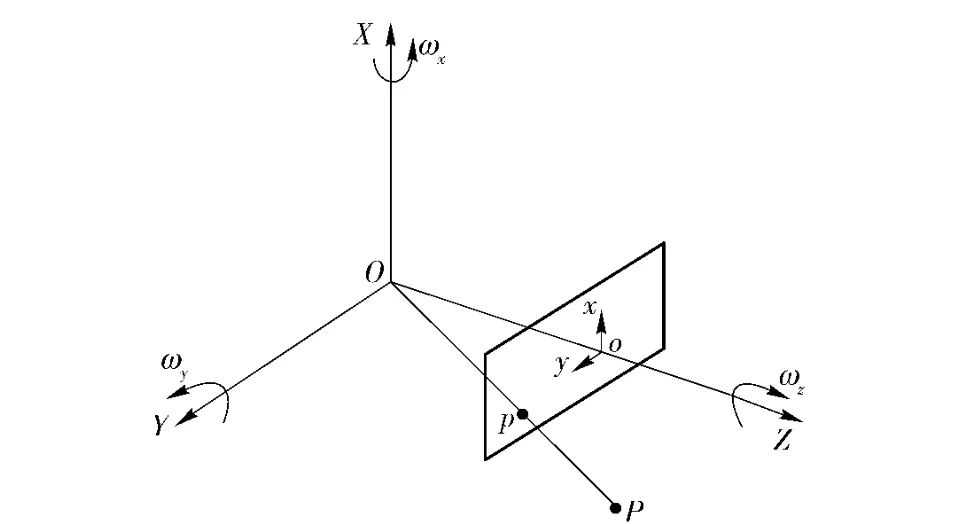
图3 摄像机投影成像示意图Fig.3 Camera projection diagrammatic sketch

当摄像机绕坐标轴发生旋转时，P 点在摄像机坐标系中的坐标变换公式为

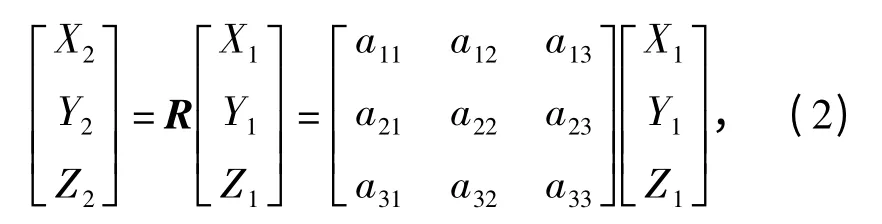
式中:(X2，Y2，Z2)为P 点在新摄像机坐标系中的坐标;R 为旋转余弦矩阵;aij为矩阵各元素值。首先考虑瞄准镜绕单一轴旋转对图像运动产生的影响，设瞄准镜绕X 轴在水平方向转动角度θ，得到

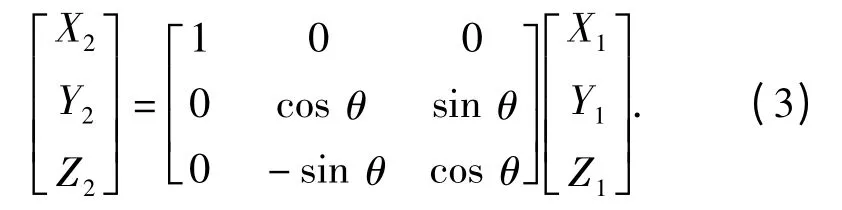
将(3)式带入(1)式，得到像点p 坐标变化公式为

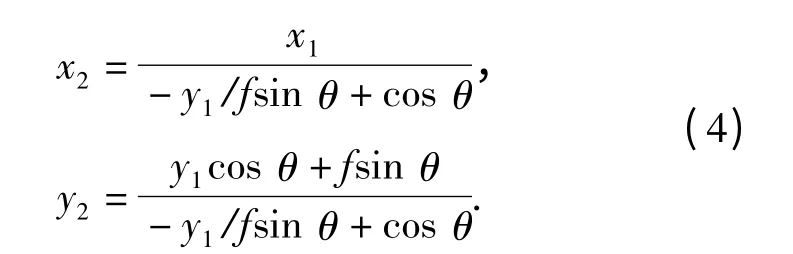
(x2，y2)表示摄像机旋转后景物点P 在像平面上所成像点的坐标。微光瞄准系统y/f≪1，且θ ＜5°时，(4)式可以近似为

同理，当随摄像机同时绕X 轴和Y 轴转动时，P点在像面坐标系中的坐标变换公式为

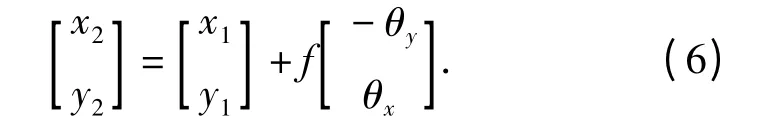
上式表示的图像运动模型符合平移变换模型，这种模型考虑了大多数情况下摄像机绕x 轴和y 轴的旋转对图像运动所起的主要作用，图像在水平面上发生整体平移，具有全局统一性，且图像特性(角度、对称性、内部结构)无任何改变，是一种刚性变换。由于(6)式利用的是陀螺仪的角度信号，在电子稳像算法中还需要将其进行必要的转换，才能作为图像的运动矢量。

2.2 陀螺仪信号的标定

陀螺仪信号的标定就是确定图像偏移量(单位:像素)与陀螺仪信号(单位:度)之间的比例系数，从而将陀螺仪测量的角度值转化为对应的图像运动矢量。

在实际稳像工况下，瞄准镜和摄像系统参数固定，因此设图像运动矢量与陀螺仪角度值之间的比例系数为常数k，其转化表达式可以写为

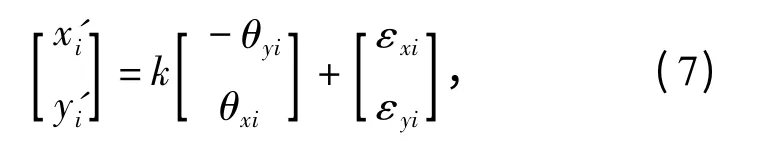
式中:(x'i，y'i)T为图像运动矢量的真实值，可以利用块匹配全搜索算法精确求得，i 为图像的帧数;(εxi，εyi)T为误差引起的陀螺仪信号转化为图像运动矢量后与真实值的残差，可以假设为零均值正态分布的高斯白噪声。如果记:a = (- θy1，θx1，…，- θyn，θxn)T，b=(x'1，y'1，…，x'n，y'n)T，则利用最小二乘法可求得:

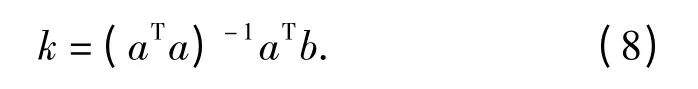
在电子稳像算法中，将k 作为常值变量乘以陀螺仪角度值，得到的就是图像运动矢量的初始估计值。

3 基于块匹配的电子稳像算法

3.1 块匹配运动估计原理

块匹配算法直接利用图像块进行相似度匹配，获得图像的全局运动矢量，是运动估计中一种简单而精确的算法［8-9］。块匹配法通常以图像的灰度值作为特征，在当前帧的搜索窗口内搜索到与参考帧中图像块灰度偏差最小的图像块，并将此图像块的位移值作为图像的全局运动矢量:如图4中，第k 帧图像中大小为M×N 参考块的中心像素坐标为(x1，y1)，在第k +1 帧图像中搜索得到的最佳匹配块的中心像素坐标为(x2，y2)，求二者之差即为图像的全局运动矢量(Tx，Ty).

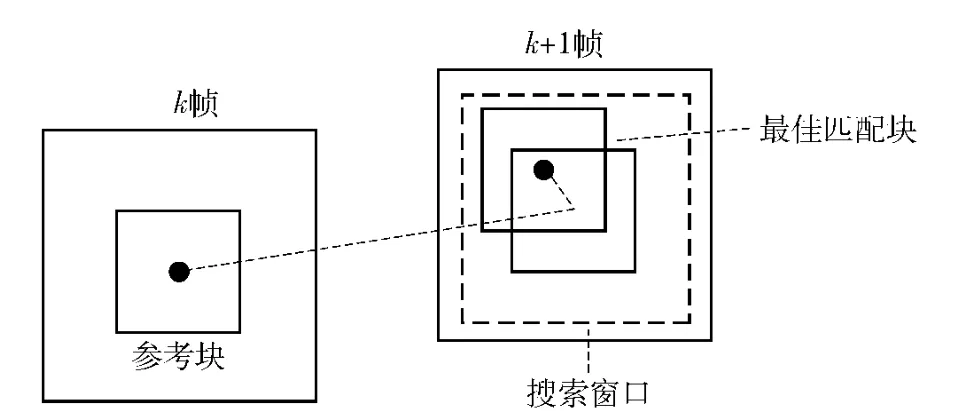
图4 块匹配运动估计原理图Fig.4 Block matching motion estimation schematic diagram

3.2 图像运动模型与匹配准则

块匹配算法多用在图像旋转角度较小且不考虑人为缩放的情况下，图像运动模型通常选择平移变换模型，与陀螺仪运动估计模型相一致。块匹配对图像运动矢量的精确估计在陀螺仪运动矢量初始估计的基础上对各种误差导致的图像残余抖动矢量进行精确估计。代入(6)式，得到图像运动模型为

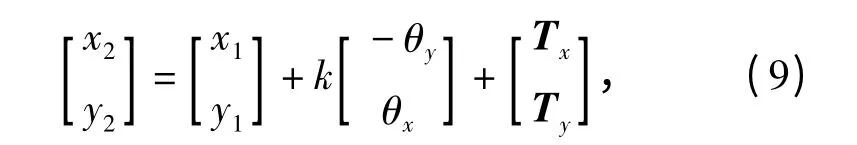
式中Tx、Ty分别表示图像在x 轴和y 轴方向残余抖动矢量。

匹配准则用于衡量两个块的相似度，不同的匹配准则，其计算效率是不一样的。目前常用的3 种匹配准则分别是:最小平均绝对差准则(MAD)、最小均方误差准则(MSE)和最多匹配像素数量(NMP)准则。实践证明，同等图像质量下，上述3种匹配准则对运动估计匹配精度的影响不是很大。由于MAD 不需要做乘法运算，硬件消耗低，兼顾了算法的速度和精确性，最适合于实时要求高的电子稳像系统。实际中常直接用最小绝对差和准则(SAD)来代替MAD，其定义为

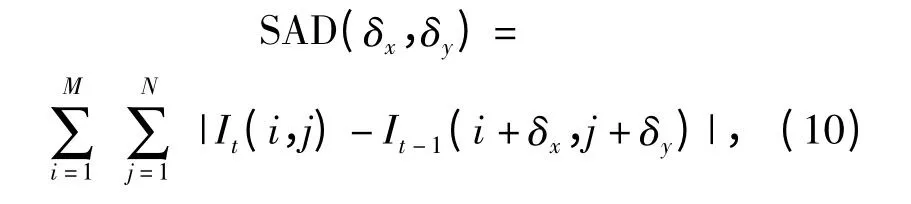
式中:M 和N 为图像块的长与宽;I(i，j)为坐标为(i，j)的像点的灰度值;(δx，δy)为运动矢量的集合。当SAD(δx，δy)达到最小值时，则此点就是所求的最佳匹配点，图像的全局运动矢量值表示为

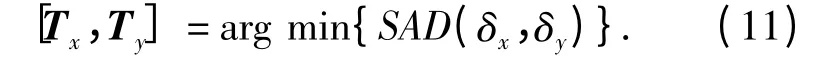
3.3 改进的菱形搜索算法

搜索方法是影响块匹配运动矢量估计速度和精度的主要因素。全搜索(FS)法虽然精度最高，但庞大的计算量限制了其在实时电子稳像算法中的应用。菱形搜索(DS)法是基于中心偏置的多级搜索方法，是目前最优秀的快速算法之一。DS 法首先利用大菱形模板进行粗搜索，当前位置SAD 最小的点将成为大菱形模板的下一个搜索中心，直至大菱形模板的中心成为SAD 最小的点;然后利用小菱形模板进一步精搜索，确定最佳匹配点位置。大菱形模板包含9 个搜索点，小菱形模板包含4 个搜索点，如图5所示。

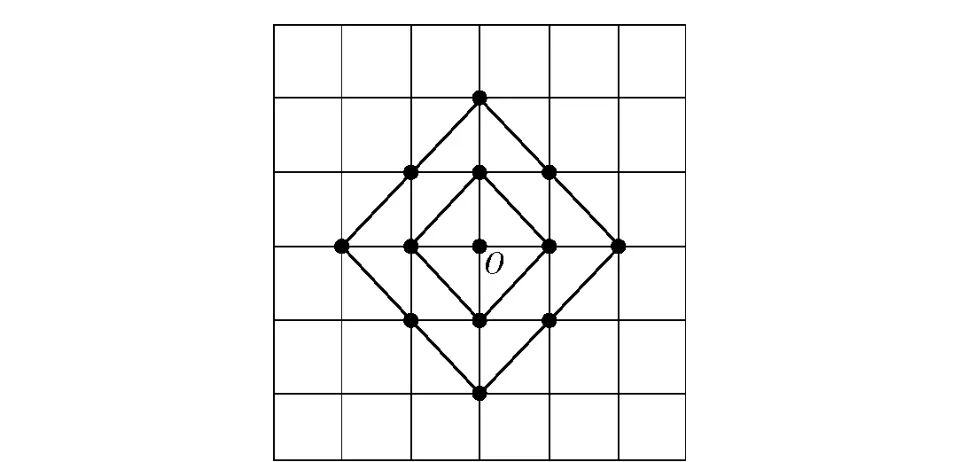
图5 菱形搜索模板Fig.5 Diamond search template

在粗搜索过程中，大菱形模板总是朝着SAD值最小点的方向前进，每次前进的距离最大为两个像素。微光图像的特点是噪声大，图像对比度差，部分位置9 个点的SAD 变化相对平坦，易使搜索停留在局部极小值点处，出现误匹配，如图6所示。

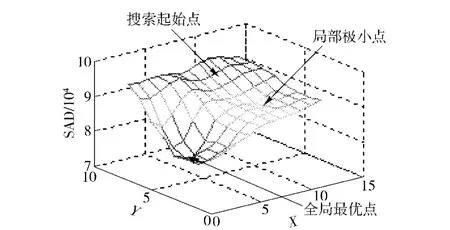
图6 菱形搜索误匹配示意图Fig.6 Matching error of diamond search diagrammatic sketch

针对DS 法的不足，提出一种基于对称校验的改进DS 法，其基本原理为:以全局最优点为几何中心，与其距离相等的各点的SAD 值应差别不大，且近似对称分布。具体方法为:在获得粗搜索匹配点后，首先以搜索起始点A 和粗匹配点O 为基础，计算等距对称点B、C、D 的坐标，如图7所示。设A 点、O 点坐标分别为(xA，yA)、(xO，yO)，则易求得C 点坐标为

B 点坐标为

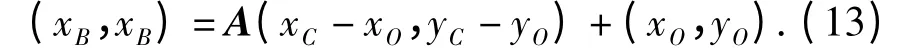
上式中，A 为余弦旋转矩阵，D 点与B 点求解方法相同。

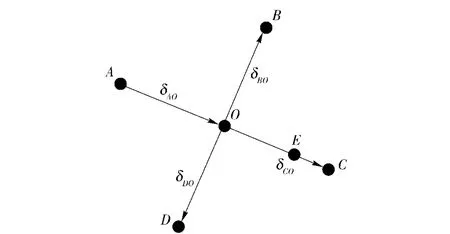
图7 基于对称校验的DS 法示意图Fig.7 Diagrammatic sketch of diamond search based on based on symmetric parity

分别计算B、C、D 各点的SAD 值，若某点与O点的差值明显小于A 点与O 点的差值，例如设置δCO＜3/5δAO，则基于对称校验原理，确定大菱形模板新的搜索中心E 点的坐标为

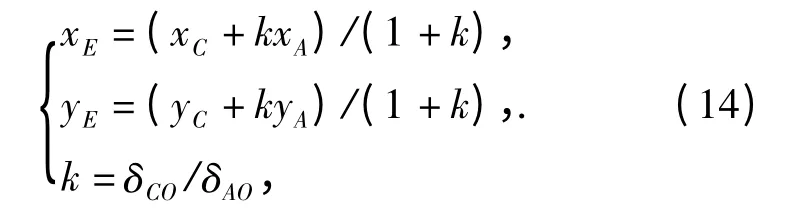
基于对称校验的DS 法具体实现步骤如下:

1)用大菱形模板进行搜索粗匹配点的坐标O，记录A、O 点的SAD 值，并计算两点SAD 值之差δAO.

2)计算B、C、D 点的坐标，并分别计算其SAD值。若其中任一点SAD 值小于O 点，以该点作为大菱形模板搜索的新起始点，返回第1)步;若任意点SAD 值与O 点的差值显著小于A 点与O 点差值，进行第3)步;若3 点SAD 值均大于O 点，跳到第4)步。

3)计算大菱形模板新的搜索中心E 点的坐标，以该点作为大菱形模板的中心，返回第1)步。

4)利用小菱形模板精搜索确定最佳匹配点位置。

分别采用传统DS 法和改进DS 法求解微光图像序列的运动矢量，并与FS 法获得的精确值进行对比，实验结果如表1所示。

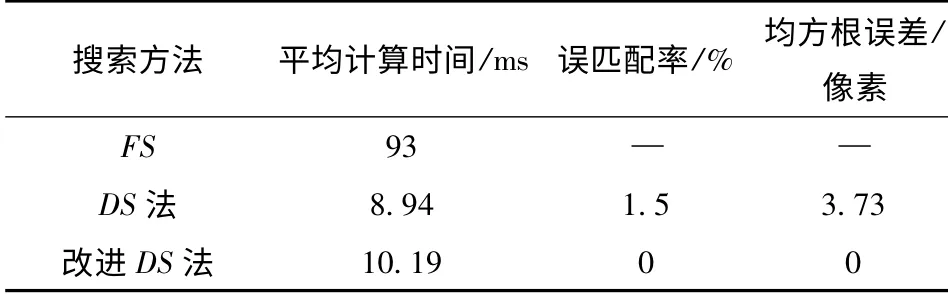
表1 改进DS 法运动矢量估计结果Tab.1 Motion vector estimation result of improved diamond search algorithm

从实验结果可以看出，DS 法大大降低了全搜索法的计算时间，但在微光图像噪声较大、对比度较差的特殊情况下可能陷入局部极小值点而导致误匹配，使运动矢量估计结果出现错误;改进DS 法由于增加了对称校验步骤，计算时间稍长，但有效避免了搜索过程停止在局部极小值点的情况，从总体上提高了算法的准确性。

4 稳像实验与分析

为检验稳像系统的性能，进行了陀螺仪信号标定和微光夜视瞄准镜的电子稳像实验，图8为微光瞄准镜电子稳像样机。

4.1 陀螺仪信号标定实验

图8 微光瞄准镜电子稳像样机Fig.8 Low-light-level telescope image stabilization prototype

利用两轴摇摆实验平台，晃动瞄准镜并实时采集陀螺仪信号和视频图像序列。然后利用块匹配全搜索算法精确确定视频中每一帧图像相对于原始帧(对应陀螺仪数值为原始零位)的运动矢量。利用(8)式求解图像运动矢量与陀螺仪角度值之间的比例系数k，并将陀螺仪信号拟合为图像运动矢量与真实的图像运动矢量进行对比，结果如图9所示。

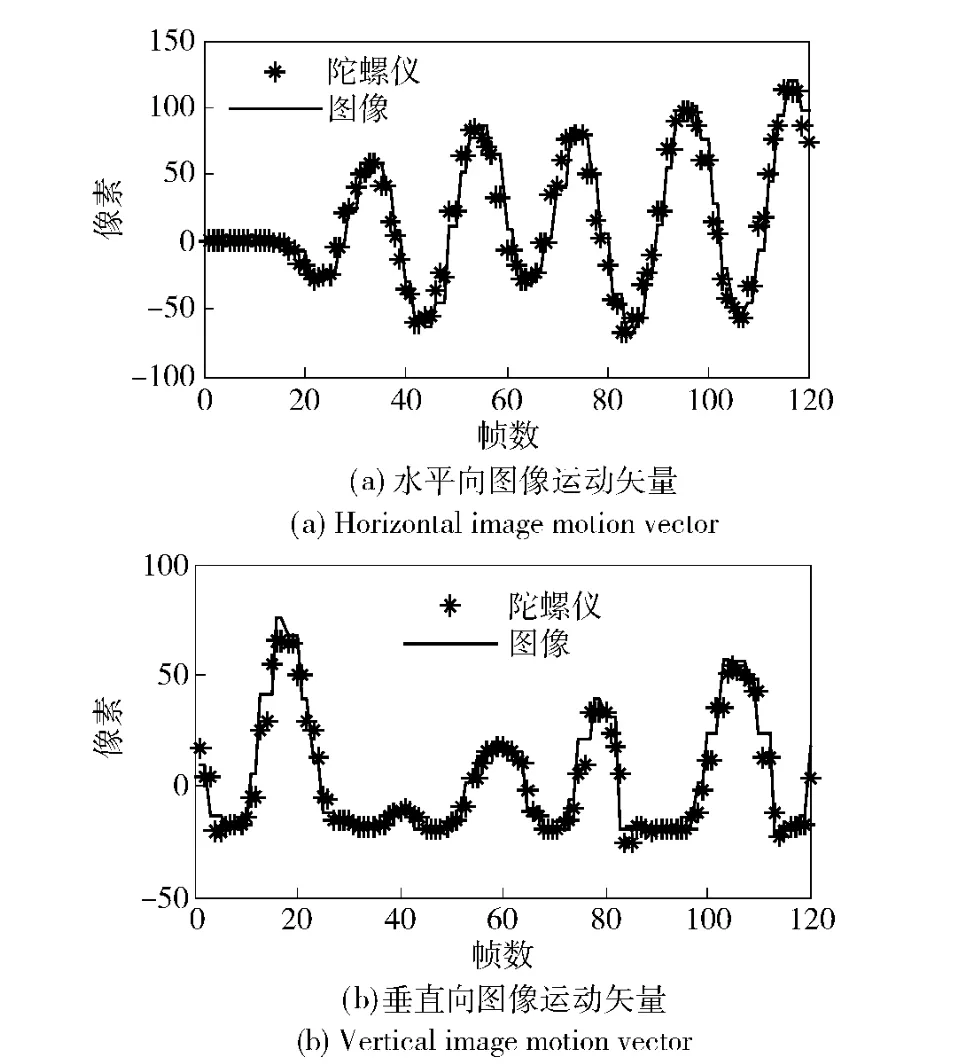
图9 陀螺仪信号的标定Fig.9 Gyro signal calibration

从图9中可以看出，陀螺仪标定的图像运动矢量和真实的图像运动矢量在幅值上具有很好的一致性，可以作为图像运动矢量的初始估计，大大减少了块匹配运算的搜索范围。另一方面，由于陀螺仪信号的随机噪声、车辆水平振动和图像运动模型等误差因素的影响，单独依靠陀螺仪获得的图像运动矢量与真实图像运动矢量之间存在一定残差，且随图像运动矢量的增大而增大，这与前文模型分析结果是一致的。因此单独利用陀螺仪信号很难完全稳定图像的抖动，需要在此基础上进一步求解图像运动矢量的精确值，才能实现对图像的精确稳定。

4.2 稳像效果分析

外界场景实验中，利用电子稳像样机采集微光瞄准镜中的图像，同时利用计算机和视频采集卡采集DSP 电子稳像模块处理前后的视频图像，结果如图10 所示。其中，水平和垂直方向的2 条白色虚线位于图像的相同位置，以此来对比图像中景物是否稳定不动。

图10 微光瞄准镜电子稳像实验Fig.10 Low-light-level telescope image stabilization experiment

电子稳像之前的微光图像序列如图10(a)所示。可以看到，随着微光瞄准镜的随机运动，图像序列中的景物也随之在水平和垂直方向晃动，乘员很难精确跟踪观察的目标，长时间的观察还容易使乘员眼睛疲劳。图10(b)为经过电子稳像处理后，乘员观察到的视频图像序列:虽然微光瞄准镜运动时，乘员观察到的场景也发生了改变，但图像中的景物不再随着瞄准镜的运动而晃动，图像内部结构也没有改变。说明经过电子稳像后，微光瞄准镜中的图像得到了有效的稳定，更加有利于乘员对目标进行观察和瞄准。

电子稳像的效果通常采用峰值信噪比(PSNR)来衡量［10］，其定义如下:

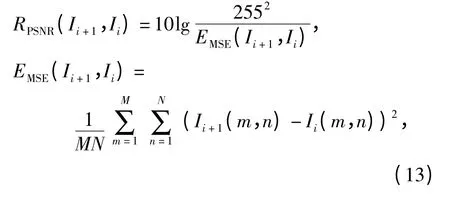
式中Ii(m，n)为第i 帧图像在(m，n)处像素的灰度值。PSNR 作为评价电子稳像算法效果的指标，将两帧图像中重合部分作为有价值“信号”，而不重合部分认为是残留的抖动“噪声”。PSNR 值越高，图像稳定效果越好，当两幅图像完全相同时PSNR 最大。

由图11 可以看到，电子稳像处理后图像序列的PSNR 较稳像之前有了大幅提高，说明了该方法能有效去除图像的抖动，实现对微光图像的稳定。

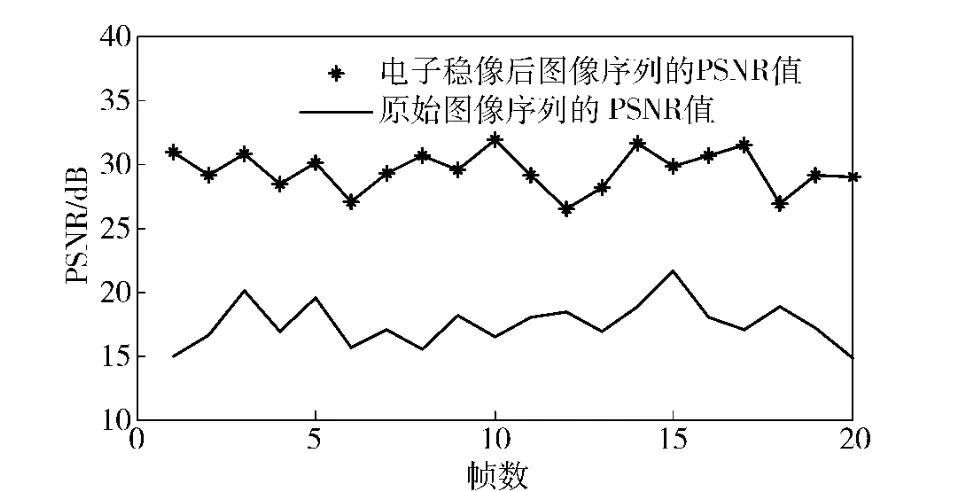
图11 电子稳像前后的峰值信噪比Fig.11 PSNR before and after electronic image stabilization

5 结论

针对“下反”稳像火控系统中微光瞄准镜不能稳像的问题，设计了独立的电子稳像系统。推导了利用陀螺仪信号进行电子稳像的转换模型，并与块匹配算法相结合完成对图像运动矢量的快速精确估计。同时基于对称校验原理改进了传统的DS 法，避免了微光图像中局部极小值点的误匹配。电子稳像实验表明，基于陀螺仪和块匹配的电子稳像技术能够对微光图像进行高精度稳定，有效提高乘员在夜间的观瞄能力。

References)

［1］ 周启煌，常天庆，邱晓波.战车火控系统与指控系统［M］.北京:国防工业出版社，2003:1 -22.ZHOU Qi-huang，CHANG Tian-qing，QIU Xiao-bo.Tank fire control and command control system［M］.Beijing:National Defense Industry Press，2003:1 -22.(in Chinese)

［2］ 朱竞夫，赵碧君，王钦钊.现代坦克火控系统［M］.北京:国防工业出版社，2003:63 -88.ZHU Jing-fu，ZHAO Bi-jun，WANG Qin-zhao.Modern tank fire control system［M］.Beijing:National Defense Industry Press，2003:63 -88.(in Chinese)

［3］ 曾雪莲，尚斐.一种新的快速智能电子稳像方法［J］.兵工学报，2008，29(11):1384 -1388.CENG Xue-lian，SHANG fei.A new fast and intelligent electronic image stabilization method［J］.Acta Armamentarii，2008，29(11):1384 -1388.(in Chinese)

［4］ 王志民，徐晓刚.电子稳像技术综述［J］.中国图象图形学报，2010，15(3):470 -480.WANG Zhi-min，XU Xiao-gang.A survey on electronic image stabilization［J］.Journal of Image and Graphics，2010，15(3):470-480.(in Chinese)

［5］ ZHU S，MA K K.A new diamond search algorithm for fast blockmatching motion estimation［J］.IEEE Trans Image Processing，2000，9(2):287 -290.

［6］ 杜登崇.面向运动场景的电子稳像算法研究［D］.北京:装甲兵工程学院，2009:21 -37.DU Deng-chong.Research on electronic image stabilization algorithms oriented to motion scene［D］.Beijing:Academy of Armored Force Engineering，2009:21 -37.(in Chinese)

［7］ 章毓晋.图像工程(下册)——图像理解［M］.第2 版.北京:清华大学出版社，2007:44 -54.ZHANG Yu-jin.Image engineering(Ⅲ)——image understanding［M］.2nd ed.Beijing:Tsinghua University Press，2007:44 -54.(in Chinese)

［8］ 郭宝龙，朱娟娟，孙伟.电子稳像的分层位平面全局运动估计算法［J］.光子学报，2009，38(11):2993 -2998.GUO Bao-long，ZHU Juan-juan，SUN Wei.Hierarchical bit-plane global motion estimation for image stabilization［J］.Acta Photonica Sinica，2009，38(11):2993 -2998.(in Chinese)

［9］ Hsu S C，Liang S F，Fan K W，et al.A robust in-car digital image stabilization technique［J］.IEEE Transaction on Systems，Man and Cybemetics，2007，37(2):234 -247.

［10］ 朱娟娟.电子稳像理论及其应用研究［D］.西安:西安电子科技大学，2009:121 -123.ZHU Juan-juan.Research on theory and application of electronic image stabilization［D］.Xian:Xidian University，2009:121 -123.(in Chinese)