基于FRFT 的几种典型相位编码信号检测与参数估计

徐会法，胡晓峰，张明智

(1.国防大学信息作战与指挥训练教研部，北京100091;2.海军航空工程学院电子信息工程系，山东烟台264001)

0 引言

多相编码(Frank 码、P1 码、P2 码、P3 码和P4码)信号是一类典型的低截获概率(LPI)雷达信号［1］。它们即具有相位跳变的特征，又具有类似线性调频(LFM)信号的时频特性，采用这类信号的LPI 雷达给雷达侦察接收机带来了新的挑战。如何在低信噪比条件下对这类信号进行检测与参数估计已成为雷达对抗界近几年研究的热点。

文献［1］分别采用Wigner Ville 分布(WVD)、Choi-Williams 分布、正交镜像滤波器组与循环平稳分析方法对多相码信号的检测与参数估计进行了分析。其中，WVD 分布受交叉项的影响，在低信噪比条件下很难提取信号参数;Choi-Williams 分布能够避免交叉项的影响，但是它的时频聚集性有所下降，降低了它的检测与参数估计性能;由于正交镜像滤波器组不具备抑制噪声的功能，正交镜像滤波器组检测算法需要对信号进行消噪处理，它的检测能力取决于信号的消噪效果;多相编码信号在频率—循环频率平面内表现出复杂的图案，从中提取信号参数也十分困难［2］。文献［1］采用在WVD 平面上搜索最大峰值的方法估计多相编码信号的载频，但是该方法易受噪声影响。文献［2］提出了一种基于Radon-Wigner 变换的多相编码信号检测与参数估计算法。文献［3］提出一种基于Radon-Ambiguity 变换的多相编码信号参数估计方法，该方法在搜索模糊函数幅度平面的直线时只需要一维搜索，计算量较小。但是，文献［2 -3］均未讨论多相编码信号载频的估计。文献［4］利用接收的信号与构造的参考信号的调制方式一致时共轭相乘的结果是正弦波这一性质，对多相编码信号的调制方式进行识别，并以该正弦波的频率作为信号载频。但是该算法假设信号的时宽已知，在实际应用中这个参数是未知的，必须通过估计得到［5］。文献［6 -8］也分别利用Wigner Ville 分布、正交镜像滤波器组与Radon-Ambiguity变换对多相编码信号的检测进行了研究。

分数阶Fourier 变换(FRFT)由于其独特的性质，特别适合处理LFM 信号［9］，并且，多相编码信号具有类似LFM 信号的时频特征，所以本文力图利用FRFT 实现多相码信号在低信噪比条件下的检测与参数估计。首先，分析了多相编码信号的时频分布特征;然后，讨论多相编码信号在FRFT 域的频谱分布特征，并且，推导出多相编码信号主要特征参数的估计表达式，最后，提出一种基于FRFT 的多相编码信号检测与参数估计算法。

1 多相编码信号模型与其时频特征

1.1 信号模型

多相编码信号模型［1］为

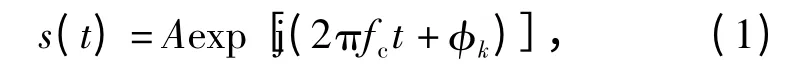
式中:A 为信号幅度;fc为载频;φk为随时间改变的相位调制函数。在一个编码周期T 内，信号的码元数为Nc，码片宽度为tb，则编码周期为

一个周期内发射信号的复包络可以表示为

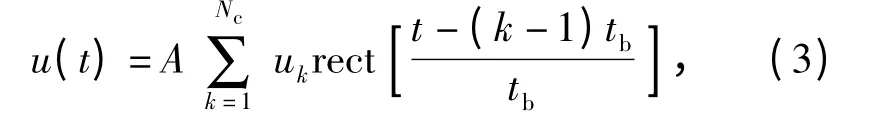
式中:uk=exp［jφk］;rect(·)为单位时宽和幅度的矩形窗。多相编码信号的调制相位φk如表1所示［1］。

表1 多相码信号的调制相位φkTab.1 Modulation phase φk of polyphase codes signals

设接收到的多相编码雷达信号为

式中w(t)是实部和虚部的方差均为σ2的加性复高斯白噪声。

1.2 信号的时频分布特征

下面分析多相编码信号的时频特征。为了避免交叉项的干扰，本文采用Choi-Williams 分布分析多相编码信号的时频分布特征。为了分析方便，假设信号不含噪声。Frank 码、P1 码、P2 码、P3 码和P4码信号的主要参数分别为:载频fc=1 000 Hz，采样频率fs=7 000 Hz，码元宽度tb=0.001 s，码元数Nc=64，编码周期T=Nctb=0.064 s.如图1和2 分别为观测时间Td=T，2T 时，各个信号的时频分布图。

如图3所示为图2(a)，为了分析方便，将其独立表示出来。

由图1和图2可看出，多相编码信号的时频分布与LFM 信号的时频分布相似，在时频平面上呈脊线分布。但是，多相编码信号的时频分布也有自己的特点，比较图1和图2，可以发现多相编码信号的时频分布具有如下特征:

1)一个编码周期的Frank 码和P3 码信号在时频平面上具有2 条主脊线和多条次脊线，而一个编码周期的P1 码、P2 码和P4 码信号在时频平面上具有一条主脊线和多条次脊线;2 个编码周期的Frank码和P3 码信号在时频平面上具有3 条主脊线和多条次脊线，而不是4 条主脊线，这是由于2 个编码周期的相邻2 条主脊线相互叠加造成的，2 个编码周期的P1 码、P2 码和P4 码信号在时频平面上具有2 条主脊线和多条次脊线。即Frank 码和P3码信号的主脊线数为信号的编码周期数+1，P1码、P2 码和P4 码信号的主脊线数为信号的编码周期数。

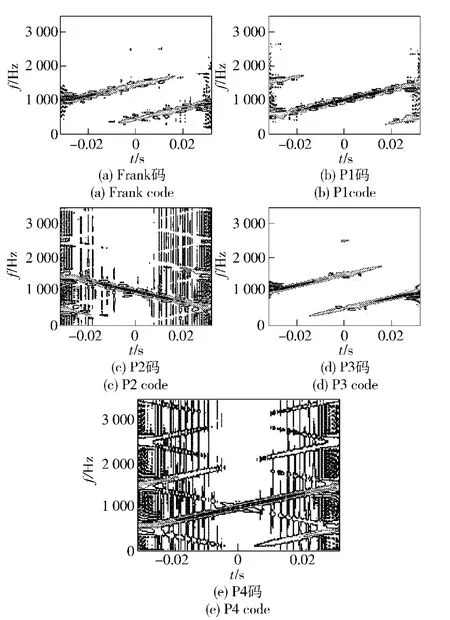
图1 Td =T 时各个信号的Choi-Williams 分布Fig.1 When Td =T，Choi-Williams distribution of polyphase codes signals

2)在时频平面上，多相编码信号的各条脊线之间相互平行，且相邻脊线之间的距离相等。正是这个特征造成了特征1)中的相邻2 个编码周期的脊线相互叠加，在图5中，2 个编码周期的Frank 码信号在其“最佳”分数阶Fourier 域的频谱分布进一步证实了该特征，2 个编码周期的尖锋相互叠加成3 个主峰和一个次峰。

3)多相编码信号在时频平面上的各条主脊线与频率f 轴的交点处频率的平均值等于多相编码信号的载频fc.由图3可以看出，Frank 码信号的载频fc=(f01+f02+f03)/3，其中f01、f02与f03是Frank 码信号在时频平面上的3 条主脊线与频率f 轴的交点处频率值。在图1与图2中，Frank 码、P1 码、P2 码、P3 码和P4 码信号的各条主脊线与频率f 轴的交点处频率的平均值也满足该特征，而且，经大量仿真进一步证实，当多相编码信号的观测时间大于一个编码周期时均具有该特征。多相编码信号在时频平面上的各条次脊线能量很小，对信号检测与参数估计影响不大，可以不用考虑。

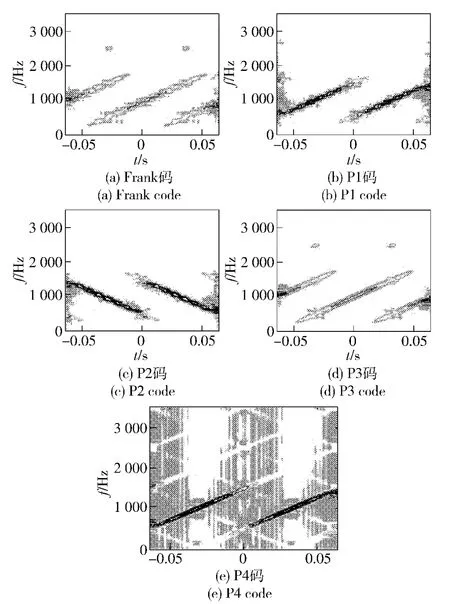
图2 Td =2T 时各个信号的Choi-Williams 分布Fig.2 When Td =2T，Choi-Williams distribution of polyphase codes signals

图3 Td =2T 时Frank 码信号的Choi-Williams 分布Fig.3 When Td =2T，Choi-Williams distribution of Frank code signal

另外，多相编码信号的每条主脊线均可看作一个LFM 信号的脊线，由文献［10］可知，利用FRFT估计得到的LFM 信号的初始频率为该LFM 信号在未经旋转的时频平面上沿其时频分布直线与频率轴交点处的频率。因此，可以利用FRFT 先估计多相编码信号的各条主脊线对应初始频率，进而再求其平均值作为多相编码信号载频的估计值。

2 多相码信号的FRFT

由文献［11］可知，FRFT 可以理解为角为α 的时频面旋转，根据该性质，以Frank 码信号为例，分析多相编码信号在FRFT 域的频谱分布特征。为了比较方便，Frank 码信号的各个参数与第1 节中的参数值相同。关于FRFT 的数值计算，本文采用文献［12 -13］提出的计算方法，信号的量纲归一化采用文献［14］提出的离散尺度变换法。信号的观测时间Td=2T，则信号的时域区间为［-T，T］.Frank 码信号的FRFT 三维分布如图4所示。在(u，α)平面上，Frank 码信号有3 个较高的主尖峰，为信号的主脊线形成的尖锋，3 个主尖峰具有相同的α 坐标，设该坐标值为α0，该角度是该Frank 码信号的“最佳”分数阶旋转角。Frank 码信号在角α0对应的FRFT内的频谱分布如图5所示，其中，3 个主尖峰为信号的3 条主脊线形成的尖峰，相邻2 个尖峰之间的距离均为Δu.

图4 Frank 码信号的FRFT 三维分布图Fig.4 Three-dimensional figure of Frank code signal’s FRFT

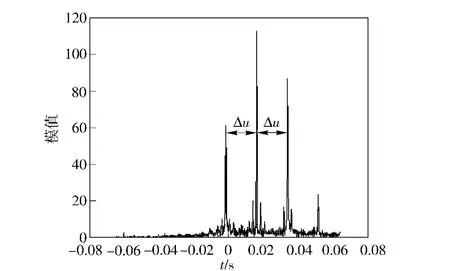
图5 Frank 码信号在角α0 =1.18π/2 的FRFT 域内的频谱图Fig.5 Spectrum of Frank code signal in the FRFT domain with angle α0 =1.18π/2

由图3与图5可知，Frank 码信号的带宽与编码周期分别为

则Frank 码信号的码元宽度与码元数分别为

另外，由文献［10，12 -15］可知，Frank 码信号在时频平面上的各条脊线的斜率，以及各条脊线与频率f 轴交点的频率值分别为

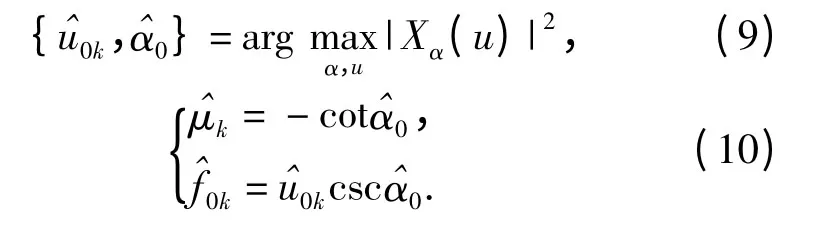
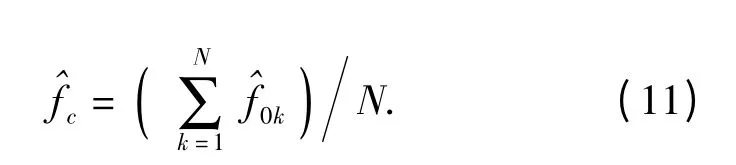
本文首次给出该结论，利用FRFT 来估计多相编码信号的载频。另外，相邻2 个f0k的差的绝对值等于多相编码信号的带宽。

因此，只要检测出多相编码信号在(u，α)平面上的各个主尖峰，并估计出相邻2 个主尖峰之间的距离，以及各个主尖峰对应的初始频率，就可以实现多相编码信号的检测与参数估计。

3 信号检测与参数估计算法

根据上文得到的结论，下面提出一种基于FRFT的多相编码信号检测与参数估计算法:

步骤1 对观测到的多相编码信号分别求旋转角α∈［0，π］的FRFT，信号长度要求包含2 个或2 个以上的编码周期。

步骤2 在平面(u，α)上进行二维搜索，获得最大峰值|Xα0(u01)|2，给定检测门限Th，由虚警概率确定，如果|Xα0(u01)|2＞Th，则说明检测到信号，进入下一步，否则退出。

步骤3 根据最大尖峰|Xα0(u01)|2在平面(u，α)上的坐标，提取信号在角α0时的FRFT 值|Xα0(u0)|2.

步骤4 对|Xα0(u0)|2采用逐次消去法，检测信号包含的所有主尖峰，直至|Xα0(u0)|2小于给定的检测门限。因为信号的能量主要集中在各个主峰上，各个主峰的高度相差不大，次峰包含的能量很小，对信号检测影响很小，所以利用逐次消去法能够检测到信号的各个主峰。

步骤5 对检测到的信号主峰，按照u 坐标由小到大的顺序进行排序，并选取与最大峰值点相邻，且峰值较大的一个峰值点，以该点与最大峰值点之间的距离作为Δu.

步骤6 依次比较两个相邻尖锋间的距离是否满足||u0k-u0k+1| -Δu|≤δ，k =1，2，…，N -1，δ 为一个较小的值，如果不满足，则将该点作为奇异点删除。

步骤7 将检测到的各个主尖峰的坐标信息(^u01，^α0)，…，(u0N，^α0)，带入(10)式与(11)式求得信号的载频估计值，将Δu 与^α0带入(5)式～(8)式求得其他参数的估计值。

对于雷达侦察接收机，信号噪声主要由接收机的内部热噪声产生，可以看作功率不变的加性高斯白噪声，而高斯白噪声在FRFT 域内仍是高斯白噪声。因此，检测门限由噪声在FRFT 域的幅度和虚警概率确定。本文采用如下方法选取Th 值:

1)选取一段与信号长度相同的高斯白噪声，对这段噪声在α∈［0，π］上依次进行FRFT，并取模值平方，然后在参数(u，α)平面上进行二维搜索，获得噪声的最大峰值。

2)对步骤1)重复进行100 次，分别得到各次噪声的最大峰值，从这100 个最大值中，再选取最大值作为虚警概率为Pf=10-2时的Th 值，如果虚警概率取Pf=10-3时，则重复进行1 000 次。

3)为了尽可能选择合理的Th 值，可以多次重复上述过程，然后，再求检测门限的平均值作为最后的Th 值。

4 性能分析与仿真验证

4.1 检测性能分析

信号检测的性能一般由检测器的输出信噪比来评估。由于多相编码信号的FRFT 比较复杂，理论分析FRFT 对多相编码信号的检测性能十分困难。文献［8］通过大量仿真验证，得到多相编码信号的Radon-Ambiguity 峰值与具有同样参数的LFM 信号的Radon-Ambiguity 峰值具有固定的比例关系ω，Frank、P1、P2、P3 与P4 码信号对应的ω 值分别近似等于0.44、0.72、0.73、0.44 和0.77.文献［2］利用Radon-Wigner 变换也得到了相同的结论。由文献［16 -17］可知，Radon-Wigner 变换与FRFT 具有等价性，即一个信号的Wigner 分布在分数阶Fourier域上的直线积分投影就是该信号在此分数阶Fourier 域上的FRFT 模的平方。因此，多相编码信号的FRFT 峰值与具有同样参数的LFM 信号的FRFT 峰值也应该具有类似的比例关系。

由文献［18］可知，对于幅度为A 的复LFM 信号，在附加复高斯白噪声条件下，FRFT 检测器对LFM 信号的输出信噪比为

式中:N 为LFM 信号的观测点数;SNRi= A2/σ20 为信号的输入信噪比，σ20为复高斯白噪声的方差。则FRFT 检测器对多相编码信号的输出信噪比为

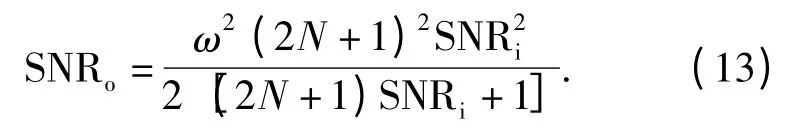
用SNRi1与SNRi2分别表示LFM 与多相编码信号的输入信噪比，SNRo1、SNRo2分别表示对应的FRFT 检测器的输出信噪比。由(12)式～(13)式可得，2 种信号在达到同样检测概率的条件下，即SNRo1=SNRo2时，2 种信号输入信噪比的关系为

当(2N +1)SNRi≫1，对(14)式两边取对数得到用分贝表示的输入信噪比关系［2］如下

由于ω ＜1，所以要达到同样的检测性能，多相编码信号比LFM 信号需要更高的输入信噪比。由4.2节的仿真结果可得，Frank 码信号要达到与LFM 信号相等的检测概率，它的输入信噪比要比LFM 信号的高7 dB，将其带入(15)式，得Frank 码信号的ω≈0.45.该结果与文献［2］得到的结果相同。

4.2 仿真验证

为了验证算法的检测与参数估计性能，取一段包含2 个编码周期的Frank 码信号为仿真对象，按照第3 节中的信号检测与参数估计算法进行仿真验证。信号的各个参数与第4 节中的参数值相同，信号的观测时间为［-T，T］.

设信号被正确检测的判断准则为:信号载频估计值的绝对误差不超过10%，即

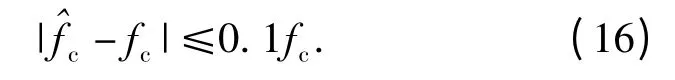
当一次信号检测满足判断准则时，则认为该次检测为正确检测。

下面利用Monte Carlo 法，信噪比从-13 dB 开始，以1 dB 为步长递增至1 dB，每个信噪比条件下模拟200 次。每个信噪比条件下，信号的正确检测概率如图6所示;信号带宽、载频和编码周期估计值的均方根误差(RMSE)如图7所示;信号带宽、载频和编码周期估计值的平均值如表2所示。

图6 当虚警概率Pf =10 -2时，信号的正确检测概率Fig.6 When false alarm probability Pf =10 -2，the signal’s correct detection probability

由图6可以看出，当信噪比大于等于-4 dB 时，该算法具有较好的正确检测概率，当信噪比等于-5 dB 时，正确检测概率降至0.73;Frank 码信号与LFM 信号的检测概率相等时，它们的输入信噪比相差7 dB.由表2和图7可以看出，信噪比为-5 dB时，信号参数的估计值还比较准确，均方根误差仍能保持较小，但是，当信噪比低于-5 dB 时，参数估计值的均方根误差已较大。随着信噪比的增加，信号的正确检测概率逐渐大，参数估计精度越来越大，从而验证了该算法的有效性。

图7 信号各个特征参数估计值的均方根误差Fig.7 The RMSE of signal’s parameters estimation results

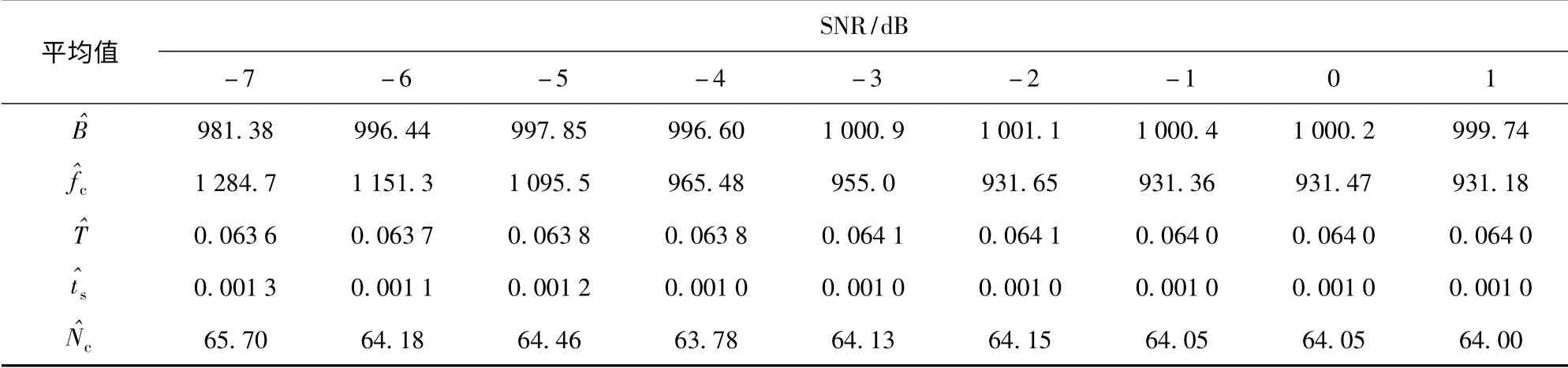
表2 信号的各个参数估计值的平均值Tab.2 Mean results of signal’s parameters estimation results

5 结论

本文分析了多相编码信号的时频分布特征，总结出多相编码信号时频分布的3 个重要特征。然后，讨论了多相编码信号在FRFT 域的频谱分布特征，推导出多相编码信号的各个主要特征参数的估计表达式。提出一种基于FRFT 的多相编码信号检测与估计算法，该算法首次给出一种利用FRFT 估计多相编码信号载频的方法。仿真结果表明，该算法在低信噪比条件下对多相编码信号仍具有较好的检测和参数估计性能。本文为多相编码信号的截获与特征提取提供了一种新方法。

References)

［1］ Pace P E.Detection and classifying low probability of intercept radar，second edition［M］.Boston:Artech House，2009:81 -119，405 -547.

［2］ 徐海源，周一宇，黄知涛，等.一种Frank 码脉压信号的检测与参数估计方法［J］.系统工程与电子技术，2007，29(6):858 -861.XU Hai-yuan，ZHOU Yi-yu，HUANG Zhi-tao，et al.Detection and parameter estimation method for Frank code pulse compression wave-forms［J］.Systems Engineering and Electronics，2007，29(6):858 -861.(in Chinese)

［3］ 徐海源，黄知涛，周一宇.基于Radon 变换的具有线性调频特性的多相编码信号参数估计［J］.信号处理，2008，24(2):172 -176.XU Hai-yuan，HUANG Zhi-tao，ZHOU Yi-yu.Parameter estimation methods for polyphase codes derived from LFM waveforms using the Radon transform［J］.Signal Processing，2008，24(2):172 -176.(in Chinese)

［4］ 邓振淼，刘渝.多相码雷达信号识别与参数估计［J］.电子与信息学报，2009，31(4):781 -785.DENG Zhen-miao，LIU Yu.Recognition and parameters estimation of polyphase-coded radar signals［J］.Journal of Electronics ＆Information Technology，2009，31(4):781 - 785.(in Chinese)

［5］ 邓振淼.雷达信号脉内分析与处理理论及算法研究［D］.南京:南京航空航天大学，2007:66 -89.DENG Zhen-miao.Study on theories and algorithms of intrapulse analysis and processing of radar signals［D］.Nanjing:Nanjing University of Aeronautics and Astronautics，2007:66-89.(in Chinese)

［6］ Milne P R，Pace P E.Wigner distribution detection and analysis of FMCW and P-4 polyphase LPI waveforms［C］∥2002 IEEE International Conference on Acoustics，Speech，and Signal Processing (ICA-SSP 02).Orlando:IEEE，2002:3944 -3947.

［7］ Copeland D B，Pace P E.Detection and analysis of FMCW and P-4 polyphase LPI waveforms using quadrature mirror filter trees［C］∥2002 IEEE International Conference on Acoustics，Speech，and Signal Processing.Orlando:IEEE，2002:3960 -3963.

［8］ Jennison B K.Detection of polyphase pulse compression waveforms using the Radon-ambiguity transform［J］.IEEE Transaction on Aerospace and Electronic Systems，2003，39(1):335 -343.

［9］ 陶然，邓兵，王越.分数阶傅里叶变换及其应用［M］.北京:清华大学出版社，2009:1 -7.TAO Ran，DENG Bing，WANG Yue.Fractional Fourier transform and its application［M］.Beijing:Tsinghua University Press，2009:1 -7.(in Chinese)

［10］ 袁伟明，王敏，吴顺君.对称三角线性调频连续波信号的检测与参数估计［J］.电波科学学报，2005，20(5):594 -597.YUAN Wei-ming，WANG Min，WU Shun-jun.Detection and parameter estimation of symmetrical triangular linear frequency modulation continuous wave signal［J］.Chinese Journal of Radio Science，2005，20(5):594 -597.(in Chinese)

［11］ Almeida L B.The fractional Fourier transform and time-frequency representations［J］.IEEE Transactions on Signal Processing，1994，42(11):3084 -3091.

［12］ Ozaktas H M，Arikan O，Kutay M A，et al.Digital computation of the fractional Fourier transform［J］.IEEE Transactions on Signal Processing，1996，44(9):2141 - 2150.

［13］ Adhemar Bultheel，Héctor E，Martínez Sulbaran.Computation of the fractional Fourier transform［J］.Applied and Computational Harmonic Analysis，2004，16(3):182 -202.

［14］ 赵兴浩，邓兵，陶然.分数阶傅立叶变换数值计算中的量纲归一化［J］.北京理工大学学报，2005，25(4):360 -364.ZHAO Xing-hao，DENG Bing，TAO Ran.Dimensional normalization in the digital computation of the fractional Fourier transform［J］.Transactions of Beijing Institute of Technology，2005，25(4):360 -364.(in Chinese)

［15］ QI Lin，TAO Ran，ZHOU Si-yong，et al.Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform［J］.Science in China:Ser.F，Information Science，2004，47(2):184 -198.

［16］ 张贤达，保铮.非平稳信号分析与处理［M］.北京:国防工业出版社，1998:186 -222.ZHANG Xian-da，BAO Zheng.Non-stationary signal analysis and processing［M］.Beijing:National Defense Industry Press，1998:186 -222.(in Chinese)

［17］ Bernardo L M，Soates O D D.Fractional Fourier transforms and optical systems［J］.Optics Communication，1994，110(5 -6):517 -522.

［18］ 齐林.基于分数阶Fourier 变换的线性调频信号的检测与处理［D］.北京:北京理工大学，2004.QI Lin.Detection and processing of linear frequency modulation signals based on the fractional Fourier transform［D］.Beijing:Beijing Institute of Technology，2004.(in Chinese)