高阻尼混凝土构件阻尼性能研究

汪梦甫，宋兴禹

（湖南大学 土木工程学院，长沙 410082）

近些年来，随着混凝土材料研究的不断深入，高性能混凝土也应运而生。高阻尼混凝土就是其中的一种。所谓高阻尼混凝土就是指通过在混凝土中掺加各种纤维和聚合物增强掺料来得到的具有较高阻尼的混凝土。与普通混凝土相比，高阻尼混凝土具有耗能能力高、抗冲击韧性好的特点［1-4］。现有的结构振动控制技术多是通过在结构中增加阻尼器来提高结构阻尼，从而达到减振的目的。如果将高阻尼混凝土应用在结构中，可以预见，结构阻尼将会有效提高，则可在不附加阻尼装置的前提下达到同样的减振效果。这既可以减少结构造价又可以避免阻尼器的安装维护带来的不便，因此具有广阔的应用前景。Wong等人［5］就强烈建议将其用于建筑结构或构件的振动控制。

国内外对高阻尼混凝土有一定的研究，这些研究（文献［2-9］）采用较为先进的研究方法，探讨不同掺料对混凝土阻尼及力学性能的影响，并试图寻求最合理的掺料配合比，以达到最大可能提高混凝土阻尼比且又不降低或尽量少降低混凝土强度的目标。尽管国内外对高阻尼混凝土构件的研究取得了较多成果，但据我们所掌握的文献资料来看，这些研究的阻尼比仅限于微幅振动的阻尼比，这在一定程度限制了高阻尼混凝土构件的推广与应用。由于混凝土结构大幅振动的环境（如强地震作用）普遍存在，且阻尼比与振动变形关系密切［11-15］，而阻尼产生耗能效应主要出现在大幅振动阶段。为了在工程实用中科学应用高阻尼混凝土，充分发挥高阻尼混凝土在大幅振动阶段的优越性能，研究高阻尼混凝土在大幅振动阶段的阻尼比变化规律与耗能能力十分必要。

基于现有的高阻尼混凝土研究成果，本文从构件角度出发，设计了一组悬臂梁振动实验，测得了钢筋、高阻尼水泥砂浆及高阻尼混凝土等构件在不同振幅下的阻尼比，绘制了构件阻尼比-层间位移角曲线。研究了聚灰比、乳液共混及不同纤维的掺入对高阻尼混凝土悬臂梁力学性能和阻尼性能的影响。在此基础上，提出了高阻尼混凝土构件阻尼比的计算理论与方法。通过与国内外相关研究的比较。

1 试验材料及试验方法

1.1 试验用原材料及配比

采用长沙坪塘水泥厂生产的32.5普通硅酸盐水泥为胶凝材料，分别掺加苯丙乳液（A）、丁苯乳液（B）、钢纤维（S）和聚丙烯纤维（F）配制高阻尼混凝土。骨料采用河沙和卵石。混凝土按C30配制，其中水泥、河沙和卵石的质量比为1∶1.23∶3.04，水灰比均为0.4，配合比见表1。表2给出了试验中采用的钢纤维和聚丙烯纤维的物理力学性能情况。

表1 高阻尼混凝土试件配合比Tab.1 Mix proportion of Concrete

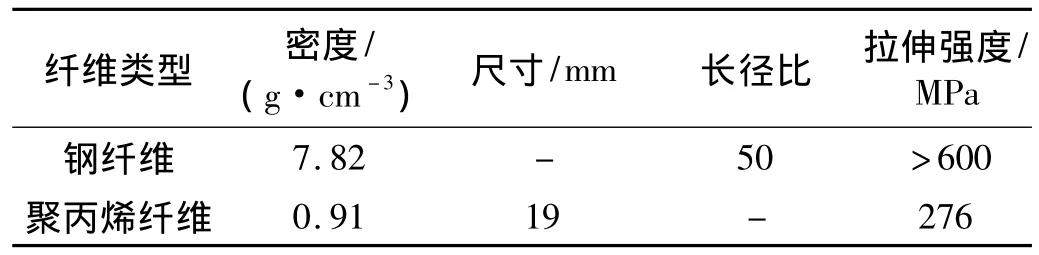
表2 试验所用纤维的性能Tab.2 Properties of fiber

1.2 试件设计及测试方法

由于本试验研究要兼顾研究对象的强度、弹性模量和阻尼三种性能，因此在试验中分别制作了3种试件。对强度及弹性模量试验，根据规范［10］的要求，分别采用150 mm×150 mm×150 mm的立方体试件和150 mm×150 mm×300 mm的棱柱体试件。对于非金属材料混凝土的阻尼性能的试验，目前国内外尚无十分成熟的方法可以借鉴，本文根据现有文献［6-8］的资料采用T型悬臂梁试件，为减小尺度效应的影响，采用大比例试件，测试长度1 000 mm，截面尺寸100 mm×100 mm，用于固定安装的部分长600 mm，截面尺寸为100 mm×100 mm，如图1所示。

对于阻尼比的测试，目前仍然是阻尼研究中的一个难点，这首先是因为阻尼不像密度、强度一样具有明确的物理意义及较好的稳定性，对同一材料采用不同的测试方法可能会得到具有较大离散性的结果；其次因为对产生阻尼的机理尚未完全明确，因此按照不同阻尼模型得到的阻尼结果也会有较大差别。为了使试验结果与现有的研究结果具有较好的对比性，本文仍然采用自由衰减法测量阻尼比。测试时，用地脚锚栓将悬臂梁固定在地槽上，采用高强钢丝悬吊重物法对悬臂梁进行加载，用百分表控制梁的顶点位移，在一定位移时释放钢丝，用DP430记录梁的加速度衰减曲线，通过该曲线就可得到梁在该顶点位移下的阻尼比和频率，试验装置见图1。不断重复上述过程，直到梁破坏为止，便可得到梁从开始到破坏全过程的阻尼变化情况。因为混凝土为脆性材料，所以为了得到梁全过程阻尼变化曲线，必须对梁进行配筋，本试验中梁采用对称配筋，两边均选配3Ф4，抗拉强度为360 MPa，弹性模量为201 GPa，箍筋采用8号铅丝，间距为200 mm。

图1 试件配筋图及加载装置Fig.1 Geometry and reinforcement details of specimens and test set-up

2 受压力学性能测试

混凝土试件的抗压强度和弹性模量均在湖南大学结构实验室完成，试验结果见表3。为了更详细的了解材料的性能，表中同时给出了不同配比混凝土梁对应顶点位移为0.1 mm时的阻尼比。

在抗压强度试验中发现，普通混凝土试块，随着荷载的增加，最后听到“啪”地一声巨响，试块被压碎，表现出明显的脆性，见图2（a）。而掺加了聚合物和纤维的高阻尼混凝土试块的破坏成断裂式，试件破坏是在自由面形成基本平行于压应力方向的裂缝造成，因为在压应力的作用下，在垂直于压应力方向的其它两个方向产生拉应变，当其达到混凝土最大拉应变时，混凝土试件破坏，见图2（b）。纤维的加入不会改变混凝土试块的破坏形式，但大大降低了破坏时裂缝数量及最大裂缝宽度，见图2（c），可见聚合物及纤维的加入对抗震是有利的。

表3 试件受压性能测试结果Tab.3 The test result of the specimens

图2 混凝土典型破坏形式Fig.2 Damage forms of cube

3 弹塑性阻尼比测试

通过本文的阻尼测试装置，可以得到构件在不同振幅下的阻尼比。基于此，本文测试了悬臂梁从完全弹性到开裂直至最终屈服全过程的阻尼比变化情况，并绘制了阻尼比-位移角曲线。为了更全面的了解钢筋以及混凝土对悬臂梁阻尼的影响情况，试验分三部分完成：首先测试不同类型钢筋的阻尼随振幅的变化情况；其次，研究不同聚灰比的砂浆悬臂梁的阻尼随振幅的变化情况；最后研究钢筋混凝土悬臂梁的阻尼随振幅的变化情况。

3.1 钢筋阻尼随位移角的变化

为了更好的了解钢筋自身的阻尼对悬臂梁在塑性阶段阻尼的影响，本文专门测试了三组不同直径，不通长度钢筋的阻尼随振幅的变化情况。试验中所用钢筋的弹性模量为201 GPa，抗拉强度为364 MPa，钢筋的直径分别为12 mm，16 mm和22 mm。每组钢筋分别采用两种不同长度，分别为20cm和40cm。试验时，将钢筋的一端焊接在钢梁上，另一端自由悬臂，在悬臂端安装加速度传感器，通过加速度衰减信号得到钢筋的阻尼，试验结果见图3，其中图3（a）和图3（b）分别表示长度20 cm和40 cm钢筋的阻尼随位移角的变化情况。

3.2 高阻尼砂浆悬臂梁阻尼随位移角的变化

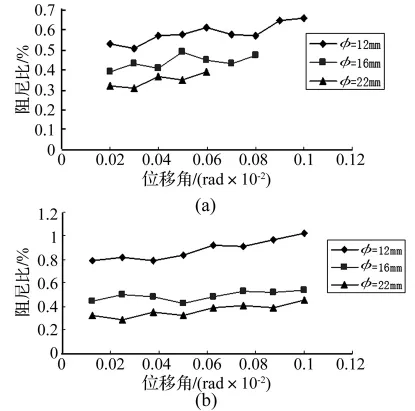
图3 钢筋阻尼值随位移角的变化情况Fig.3 Amplitude-dependent damping characteristics of rebar

因为砂浆同混凝土具有相似的性能，研究砂浆的阻尼性能对研究混凝土具有借鉴意义。本文通过对一组砂浆悬臂梁的在不同顶点位移下自由振动衰减测定，比较了不同聚灰比下水泥砂浆构件阻尼比随振幅的变化情况。试验中采用32.5普通硅酸盐水泥为胶凝材料，采用苯丙乳液为聚合物掺料，细骨料采用ISO标准砂。试验中配制四组砂浆悬臂梁试件，固定水泥和砂的质量比为C/S=1/3，水灰比均为0.4，聚灰比分别为0%，10%，15%，20%，试件编号分别记为 S00，S10，S15，S20。采用T型试件测试阻尼性能，悬臂端尺寸为30 mm×50 mm×300 mm，夹持端尺寸为30 mm×30 mm×100 mm。试验结果见图4。

3.3 高阻尼混凝土悬臂梁阻尼随位移角的变化

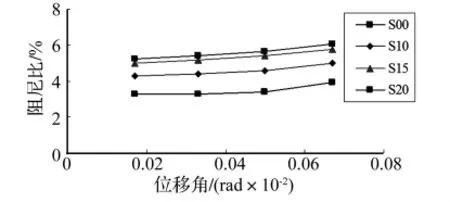
图4 高阻尼水泥砂浆试件阻尼比随位移角的变化情况Fig.4 Amplitude-dependent damping characteristics of mortar cantilever beams

钢筋混凝土悬臂梁阻尼试验同样分为三组，第一组主要考虑聚合物乳液含量的变化对阻尼比的影响，第二组主要考虑两种乳液共混时对阻尼比的影响，第三组主要考虑两种纤维的加入对阻尼比的影响。试验结果见图5～图7，其中（a）图表示弹性阶段的阻尼比变化情况，（b）图表示开裂阶段阻尼比的变化情况。

图5 聚合物含量对阻尼比的影响Fig.5 The effect of polymer-cement ratio on amplitude-dependent damping

图6 乳液共混对阻尼比的影响Fig.6 The effect of latex blend on amplitude-dependent damping

3.4 钢筋混凝土悬臂梁基频随位移角的变化

图7 纤维对阻尼比的影响Fig.7 The effect of fiber on amplitude-dependent damping

在测量悬臂梁的阻尼比随位移角的变化曲线过程中，同时得到了梁的基频随位移角的变化情况。测量梁的基频的变化情况主要出于两方面的考虑：首先，通过基频的变化可以判断构件所处的受力阶段；其次，由结构动力学可知，悬臂梁的基频正比于梁刚度的平方根，所以基频的变化情况反映了构件刚度变化情况。图8给出了悬臂梁基频随位移角的变化情况，其中图8（a）反映了聚灰比对频率的影响，图8（b）反映了纤维对频率的影响。

图8 基频随位移角的变化情况Fig.8 Amplitude-dependent basic frequency characteristics of cantilever beam

4 试验结果分析与讨论

4.1 试验结果分析

从表3可以看出，提高聚灰比可以有效增大混凝土的阻尼比，但同时混凝土的强度和弹性模量会有较大的降低，要兼顾混凝土的强度和阻尼性能，聚灰比要控制在一定的范围内。从试验结果可以看出，最优聚灰比应该控制在10%～15%之间。在聚灰比相同时，采用共混乳液代替单一乳液可以在一定程度上缓解高阻尼混凝土强度和阻尼性能不能兼顾的矛盾。从PAB12，PABS，PABF三组试件试验结果可以发现，纤维的加入对提高混凝土的抗压强度和弹性模量效果不大，但可以提高混凝土在弹性阶段的阻尼性能。同时，从表中还可以看出，聚灰比会影响混凝土的变形能力，且聚灰比越大影响越明显。在聚灰比较小时，影响混凝土的变行能力的主要因素是强度，强度越大变形能力越大；在聚灰比较大时，随着聚灰比的提高，虽然混凝土的强度有较大降低，但峰值应变仍能保持在较大水平，说明聚合物的添加对混凝土的变形能力是有利的。在聚灰比相同时，纤维的加入也可以改善混凝土的变形能力。

从图3可以看出，各组钢筋的阻尼值相对混凝土阻尼值而言均较小，虽然钢筋阻尼比随位移的增大也有所增大，但增幅较小，因此钢筋阻尼比可以认为是一个常值。而从图5～图7可以看出，悬臂梁的阻尼比随着顶点位移的增大而增长，特别在开裂以后，增长更加明显。基于此，本文认为钢筋自身的阻尼对悬臂梁阻尼的影响较小，可以忽略。

从图4可以看出，聚灰比对砂浆的阻尼改善效果较为明显，但聚灰比过大时对阻尼的改善效果会降低，聚灰比的合理数值在10%～15%之间。从图中还可以看出，随着振幅的增大，砂浆阻尼比增大，但开始阶段增长较为平缓，随后增幅变大。本文认为，随振幅的增大，构件内部会出现越来越多的微裂缝，振动时微裂缝之间的摩擦是造成阻尼增大的主要原因。

从悬臂梁阻尼试验的三组曲线可以发现，阻尼比随位移角的增大而增大。在弹性阶段，各组试件的阻尼比随位移的变化幅度相对较小，相对而言，聚灰比较高的混凝土阻尼比随位移增加的幅度更大一些，乳液混合的方法对混凝土阻尼比的变化趋势基本无影响，而在相同条件下加入纤维后阻尼比随位移的增长趋势明显趋于平缓，说明纤维的加入会对阻尼的增长有约束作用。进入开裂阶段后，随位移的增大各组混凝土阻尼比会有大幅提高，且在开裂阶段后期阻尼比的提高尤为明显。从图5（b）可以看出，在开裂阶段的前半段，虽然高聚灰比的混凝土仍表现出较好的阻尼性能，但不同聚灰比混凝土的阻尼比随位移增加的幅度相差不大，在开裂阶段的后半段，不同聚灰比混凝土的阻尼比表现出较大的随机性。从图6（b）可以看出，在聚灰比相同时，采用乳液混合的混凝土同单一乳液混凝土的阻尼比变化趋势相同。从图7（b）可以看出，在聚灰比相同时，纤维的加入对开裂阶段的阻尼比有较大影响，随位移的增大，添加了纤维的混凝土的阻尼比的增长幅度小于未加纤维的，在开裂阶段后期这种趋势更加明显。

从图8可以看出，在弹性阶段，基频基本保持不变；进入开裂阶段后，随位移角的增大，频率开始减少，但减小趋势较为缓慢；在临近屈服阶段，基频会有较大降低。通过频率的变化情况就可以判断构件所处的受力状态。另外，频率的变化还反映了构件刚度的变化。从图中可以看出，虽然乳液的加入会降低构件初始阶段的刚度，但却可以提高构件在临近破坏时的残余刚度，而且随聚灰比的增大，残余刚度提高越多，这对抗震是有利的。从图8（b）可以看出，在聚灰比相同时，纤维的加入对构件刚度的提高是有利的，特别是钢纤维的加入对构件的初始刚度和残余刚度都有较大提高，聚丙烯纤维的加入可以有效提高构件的残余刚度。

4.2 悬臂梁阻尼比三折线模型

通过以上悬臂梁全过程阻尼比的分析，本文认为，构件的阻尼比主要包括两部分：材料阻尼和摩擦阻尼。此处所指的材料阻尼包括混凝土本身各相之间的界面摩擦，钢筋阻尼以及高分子材料通过分子键或物理键所耗散的能量产生的阻尼，摩擦阻尼是指由于混凝土的开裂以及钢筋的粘结滑移产生的阻尼。为了便于研究，本文做以下假定：材料阻尼不随构件振幅的变化而变化，摩擦阻尼是阻尼比增大的主要原因。

在弹性阶段，材料阻尼是构件阻尼的主要来源，只是随着梁位移角的逐渐增大，在梁中会形成一些微裂缝，从而导致摩擦阻尼的影响增大，在宏观上表现为构件的阻尼比增大，直到开裂阶段；在开裂阶段前期，随着裂缝的开展，摩擦阻尼的影响越来越大，但总体上说阻尼比的增长还较为平缓；在开裂阶段后期裂缝开展已经十分明显，构件的阻尼比以摩擦阻尼为主，宏观上表现为阻尼比有较大幅度增长。需要说明的是，虽然钢筋自身的阻尼对混凝土阻尼的影响可以忽略，但是配筋率的影响不能忽略，因为配筋率会影响悬臂梁的开裂与屈服，影响裂缝的发展，最终会影响构件的摩擦阻尼。

将构件的材料阻尼记为ξm，摩擦阻尼记为ξf，则构件的阻尼比可表示为：

构件的开裂位移角，屈服位移角及中值位移角分别记为θc，θy和θz，其中θz=（θc+θy）/2，三个位移角对应的阻尼比分别记为ξc，ξy和ξz，以上述三个点可以将阻尼比-位移曲线分为三个阶段，如图9所示。

记：

由式（1）、式（2）、式（3）可得：

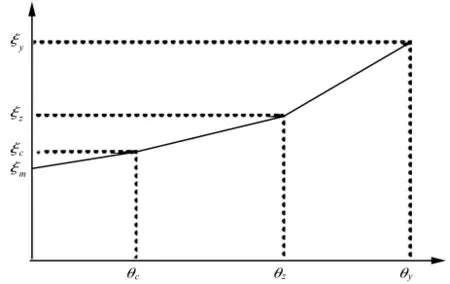
图9 阻尼比三折线模型Fig.9 The trilinear model of damping ratio

只要确定各阶段α、β的值，就可以得到构件的阻尼比。假设α仅与构件本身的配筋及骨料情况有关，可以通过统计的方法得到，根据本文试验结果α取值在1.5～3之间。基于以上假设，只要给出β的计算方法，就可得到各阶段构件阻尼值。对于β的确定，本文对实测数据进行线性拟合，给出了各阶段的计算公式：

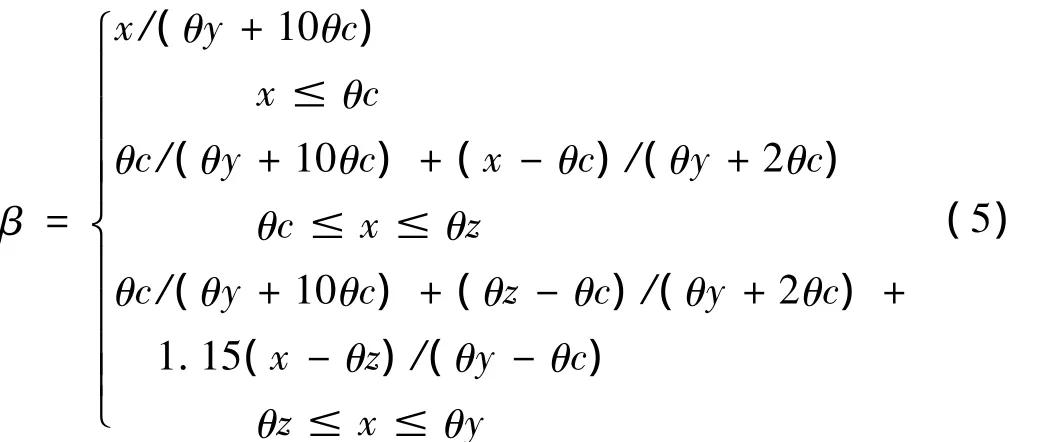
将（5）式带入（4）式，并分别取x值为θc，θy和θz，即可得到开裂位移角，中值位移角和屈服位移角对应的阻尼比，本文根据试验结果近似取θy=10θc，得到如下简化计算公式：

根据式（6）～式（8）可以很容易得到阻尼比随位移的全过程曲线。图10给出了PT和PA12两组悬臂梁的实测曲线与本文提出的三折线模型的对比情况。

从图10可以看出，当α分别取2.5和1.5时，本文所提出的三折线模型曲线与实测曲线符合良好，证明了本文提出的阻尼模型可以在一定程度上反应构件阻尼比在开裂阶段的发展趋势。但同时可以看出，α的取值对本文提出的阻尼模型曲线的影响较大，特别是在开裂阶段后更为明显。本文通过对九组实测曲线和三折线模型的对比发现，当材料阻尼较大时α取小些，当材料阻尼较小时α取大些这样得到的三折线更接近真实曲线。

4.3 三折线模型与现有阻尼比计算公式的对比

目前人们对混凝土材料的阻尼特性并没有充分的认识，国内外关于阻尼研究的重点集中在结构模态阻尼比的实测与计算等方面。

Davenport和 Hill-Carroll［2］以 151 座建筑物的 522个阻尼数据为基础，率先建立了结构基本模态阻尼比计算公式：

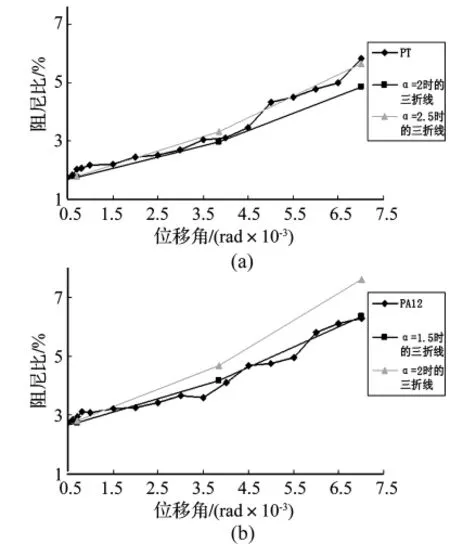
图10 混凝土悬臂梁实测阻尼比曲线与本文模型曲线对比Fig.10 A comparison of damping ratio between the field curve and the trilinear model

式中，Δ为结构顶层位移（单位：mm），H为建筑物高度（单位：m）。

Jeary［13-14］以8座建筑物的86个阻尼数据为基础，建立了与振动幅值相关的三段式阻尼比计算模型，其中，低幅阶段、高幅阶段为常量阻尼比，而中幅阶段阻尼比的计算公式为：

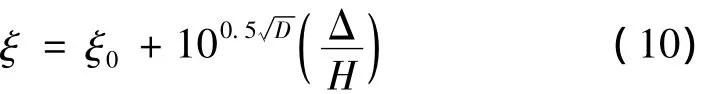
式中，D为建筑物振动方向的平面几何尺度，ξ0为低幅振动时的阻尼比。

上述有关钢筋混凝土结构基本模态阻尼比的计算公式，都是基于建筑物风试验所得模态阻尼比数据为基础，由于这些风脉动引起的振幅很小，因此，这些公式适用于完全弹性钢筋混凝土结构基本模态阻尼比的计算。同时，上述研究都表明，钢筋混凝土结构的模态阻尼比是振幅的函数，振幅越大，阻尼比越大，这与本文试验结果相符。

虽然上述公式是用于计算结构的阻尼比，但对于构件阻尼比的计算也有一定的借鉴意义，因此本文给出了采用上述公式计算的弹性阶段的阻尼比曲线与试验曲线和采用本文曲线计算的对比图，见图11。其中，Jeary曲线中ξ0=ξm，且取其上升段进行比较。

图11 不同阻尼比计算模型曲线对比Fig.11 A comparison of different damping ratio model

从图11可以看出，虽然Davenport曲线和Jeary曲线都是基于建筑物风试验所得模态阻尼比数据为基础的，但都可以反映悬臂梁在弹性阶段的阻尼比随振幅的变化情况。Davenport曲线形式简单且结果唯一，具有较好的适用性，但其仅考虑了振幅的影响，未考虑材料阻尼的影响，因此精确性偏低。Jeary曲线采用三段式阻尼比计算模型，本文在低振幅区段（Δ/H≤0.1×10-3）时，取ξ0=ξm，得到的不同高阻尼混凝土悬臂梁上升段阻尼曲线与实测结果均较为接近，可见，考虑材料阻尼影响后的Jeary曲线比Davenport曲线具有更好的精度。与以上两种阻尼模型相比，本文提出的阻尼模型具有更好的灵活性，当选用合适的计算参数时，可以得到更为准确地阻尼结果。

5 结论

混凝土是建筑结构中使用最广泛的的材料，改善混凝土材料的性能对提高结构的整体性能具有重要作用。基于此，本文配制了九组不同配比的高阻尼混凝土，并对其进行了力学性能及阻尼性能的研究，通过对比分析找到了可同时兼顾混凝土强度及阻尼性能的最优聚灰比的范围在10%～15%之间。这对高阻尼混凝土在工程中的广泛应用具有一定的借鉴意义。

此外，文中还首次测得了构件阻尼比随振幅的变化情况，探讨了阻尼的产生机理和阻尼影响因素，提出了阻尼比全过程的三折线简化模型，给出了简化模型的参数计算公式，通过与国内外相关研究的比较，校验了本文模型的正确性。而现有的设计中仍然采用的是常阻尼比，这与实际情况不符，本文阻尼模型的提出对现有的常阻尼比设计向振幅相关阻尼比设计的发展具有一定的参考价值。

［1］欧进萍，关新春.土木工程的智能结构体系研究与发展［J］.地震工程与工程振动，1999，（2）：21-28.

［2］Fu X L，Chung D D L.Vibration damping admixture for cement［J］.Cement and Concrete Research，1996，26：69-75.

［3］ Fu X L，Li X H，Chung D D L.Improving the vibration damping capacity of cement［J］.Materials Science，1998，33：3601-3605.

［4］Qrak S.Investigation of vibration damping on polymer concrete with polyster resin［J］.Cement and Concrete Research，2000，（30）：171-174.

［5］Wong W C，Fang P，Pan J K.Polymer effects on the vibration damping behavior of cement［J］.Journal of Materals in Civil Engineering，ASCE，2003，554-556.

［6］柯国军，郭长青，胡绍全，等.混凝土阻尼比研究［J］.建筑材料学报，2004，7（1）：35-40.

［7］万泽青，刘 平，施 伟.高阻尼混凝土的试验研究及阻尼机理探讨［J］.混凝土，2007，（7）：37-40.

［8］刘铁军，欧进萍.水泥砂浆强度和阻尼增强掺料及试验［J］.低温建筑技术，2003，（1）：7-9.

［9］钟世云，陈志源，康 勇，等.聚合物乳液共混物及其改性水泥砂浆的力学性能［J］.混凝土与水泥制品，2002，（1）：10-14.

［10］普通混凝土力学性能试验方法标准.GB/T 50081-2002.

［11］尚世英，董至仁.钢筋混凝土构件阻尼值试验研究［J］.工程抗震，1993，12（4）：18-19..

［12］ Davenport A G，Hill-Carroll P.Damping in tall buildings：its variability and treatmentin design［J］.ASCE Spring Convention，Seattle，USA，Building Motion in Wind，1986，42-57.

［13］ Jeary A P.Damping in tall buildings：a mechanism and a predictor［J］.Earthquake Eng.Struct.Dyn，1986，14：733-750.

［14］ Jeary A P.The description and measurement of nonlinear damping in structures［J］.J.Wind Eng.Ind.Aerodyn，1996，59：103-114.

［15］ AIJ（2000）damping in buildings［S］.Architectural Institute of Japan，Tokyo（in Japanese），2000.