转子-轴承系统混沌运动的神经网络反馈控制方法

张顺浩，郑铁生

（1.朝鲜理科大学 数学及力学系，朝鲜平壤恩情区；2.复旦大学 力学与工程科学系，上海 200433）

在具有滑动轴承的转子系统中，油膜力是转子失稳的主要因素之一。当系统某些参数（旋转速度，间隙等）改变时，系统会发生倍周期或概周期分岔直至进入混沌运动。因此研究该类系统的振动特性，稳定性及其控制一直是转子动力学的重要课题。国内外许多文献对该类系统进行了研究。Shen等［1］用基于变分不等方程的油膜力计算方法分析了转子-轴承系统的非线性动力学特性；平衡转子的Hopf分叉，不平衡转子的周期振动，概周期振动和混沌振动。徐小峰和张文［2］指出对于不平衡转子-轴承系统，随着质量偏心的增大，运动变得复杂，随着转速的增大，周期涡动，倍周期分叉，混沌运动交替出现。近年来，应用电磁力作为控制力源的电磁主动控制引起许多学者的重视。Das［3］和 Chen-Chao Fan 等［4］在转轴上设置了电磁激励机，研究了转子-轴承系统振动控制方法。利用转子-轴承系统的周期振动反馈信号和预知的反馈控制强度，实现激励机极线圈电流的PD控制，使转子和极表面之间的电磁力抑制转子周期振动的振幅，但未涉及系统混沌运动的控制。

神经网络已被广泛应用模式识别和图像处理，控制和优化，预报和智能信息管理以及通信空间科学等领域［5-6］。Ramesh 等［7］把神经网络跟 OGY 控制方法和Pyragas的反馈控制方法分别结合，研究了VDP振动子的控制问题。谭文和王耀［8］用人工神经网络，实现了Henon映射混沌运动的控制。Qin等［9］提出了一个用BP神经网络控制混沌举动的方法。这些方法所针对的非线性方程具有解析式简单，目的状态明确的特点，因此其混沌运动也易于控制。

本文将Pyragas的反馈控制方法［10-11］和神经网络结合，在反馈控制强度的计算上采用间接误差计算的BP算法和自适应学习率的BP算法结合而形成的改进型BP神经网络方法，不需要较多的系统先验知识，比如，油膜力的解析表达式，不稳定周期轨道等，因而更能适应工程转子-轴承系统混沌振动控制的实际要求。用此改进型BP神经网络方法研究了一个具有两个自由度的非线性转子-轴承系统的混沌振动控制问题，以神经网络控制代替反馈控制强度的复杂计算过程。即当嵌入在混沌吸引子中的不稳定周期轨道未知的情况下，以系统输出的混沌信号为网络输入，通过神经网络学习追寻滞延反馈控制强度，把反馈控制信号施加到转子上以消除混沌运动，使嵌入在混沌吸引子中的不稳定周期轨道回到稳定周期轨道上。

1 转子－轴承系统的数学模型

Jeffcott刚性转子-轴承系统动力学模型如图1所示。图中，O为轴瓦几何中心，O-x1x2静止坐标系；Oj为轴颈几何中心；Oc为转子质心；G=1/（σm）为无量纲载荷；fx1和fx2分别为无量纲非线性油膜力的水平，垂直分量；ω为转子角速度。

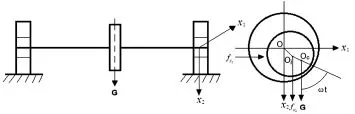
图1 Jeffcott刚性转子-轴承系统动力学模型Fig.1 Configuration of Jeffcott rotor-bearing system

无量纲形式的Jeffcott刚性转子-轴承系统状态方程为：

其中：

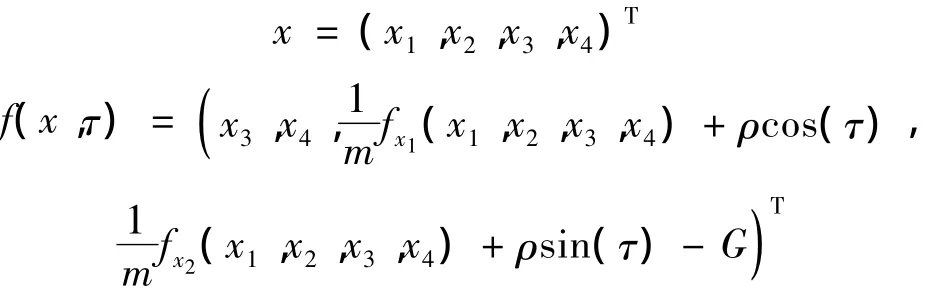
非线性油膜力和，由文献［12-13］确定为：

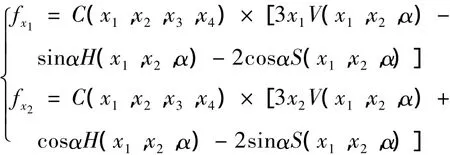
其中：

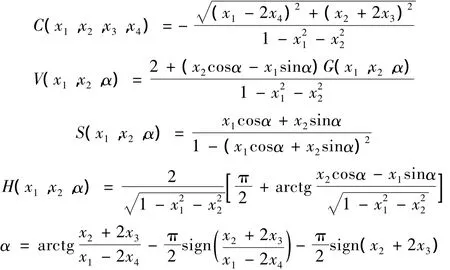
2 控制系统和神经网络学习

根据非线性方程（1），变量x1，x2相互耦合。因此只针对一个变量实施反馈控制，就能达到控制系统振动的目的，这样在实践中也更易于实行。反馈控制采用文献［3-4］方案，如图2所示。设x0（τ）是方程（1）的不稳定周期轨道，并且系统已进入混沌运动x（τ）。我们的目的是通过实施反馈控制，使混沌运动重新回归稳定周期运动。

系统的反馈控制方程可写为：

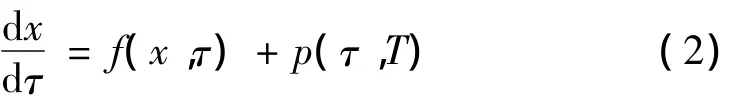
其中Dxf（x0（τ），τ）为非线性函数f（x，τ）的雅可比矩阵，显然它是T周期函数。根据Floquet理论，上述方程（3）有正规解 δx=exp（s，τ）y（τ），其中s为 Floquet指数，函数y（τ）为T周期函数。于是方程（2）中的反馈项为：

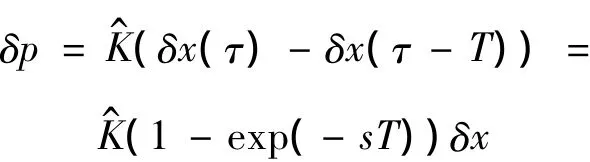
从而得到方程（2）的周期变系数线性微分方程：

该方程的Floquet乘子λ=exp（sT）和反馈强度k之间满足如下关系：

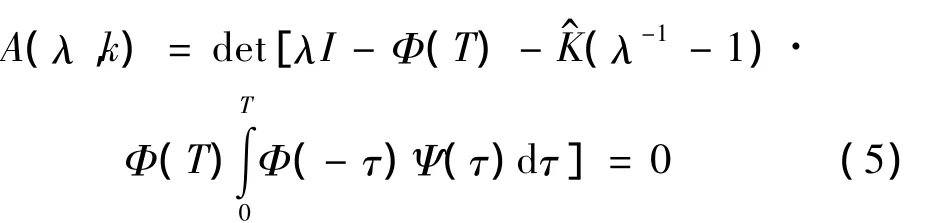
式（5）的Φ，Ψ分别为方程（3）和方程（4）的基本解矩阵，分别由下面的矩阵线性微分方程确定：

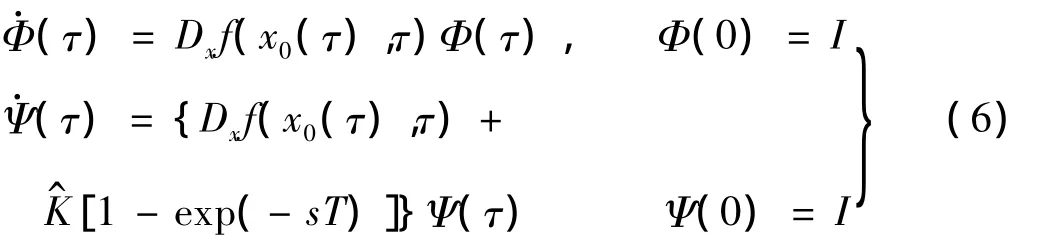
采用神经网络的控制系统的框图和实现方案如图2所示。

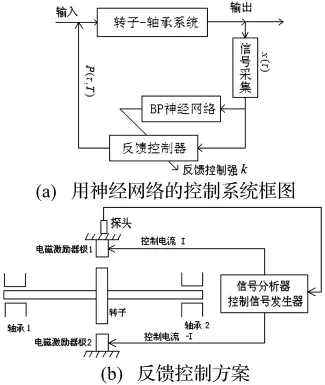
图2 用神经网络的控制系统框图与反馈控制方案Fig.2 Diagram of chaos control system using neural net and feedback control scheme

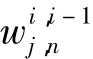
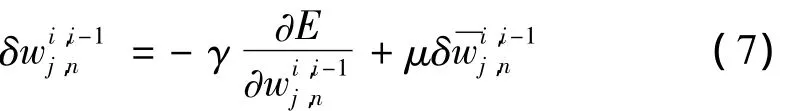
上式中E为输出层的学习误差；0＜μ＜1为惯性系数，可提高收敛速度，抑制寄生振荡，改善动态性能；0＜γ＜1为学习率，为加快算法的收敛速度，令：

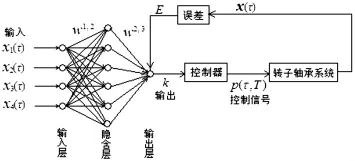
图3 具有2层的BP神经网络的结构和学习Fig.3 Back propagation neural net course

3 数值仿真

取m=70，σ =0.1，由文献［13］可知：当 0.05 ＜ ρ＜0.1时，系统（1）处于周期运动状态；当 0.1＜ρ＜0.245时，处于倍周期分叉状态；当0.245 ＜ρ＜0.26 时，处于概周期运动状态；当0.26＜ρ＜0.37时，处于混沌运动状态；当0.37＜ρ＜0.5时，为周期运动状态。当ρ=0.31 时，x1（τ），x2（τ），的时域波形，功率谱，轴心轨迹分别如图4所示。

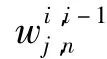
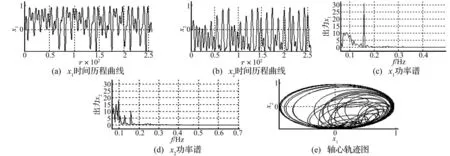
图4 控制前的系统的响应（ρ=0.31）Fig.4 The system response without control（ρ=0.31）

图5 控制x1的过渡期和结束后的系统的响应Fig.5 The system response with control of x1

4 结论

本文采用改进型BP神经网络方法，实现了刚性Jeffcott转子-轴承系统的混沌振动控制。当无量纲偏心为ρ=0.31时，系统进入混沌运动。引入滞延反馈控制，通过间接误差计算的BP神经网络学习方法和自适应学习率BP算法，获得恰当的反馈控制强度，使嵌入在混沌吸引子中的周期为2π的不稳定周期轨道回到稳定周期轨道上。在网络训练过程中，根据转子-轴承系统的输出，自动追寻滞延反馈控制强度。从数值仿真曲线可知，该方法具有控制反应快，所施控制小的特点，控制效果跟控制变量的选择无关。特别是，对工程实际转子-轴承系统，采用电磁激励器控制，对于油膜力无解析表达式，而且不稳定周期轨道未知的场合，该方法尤为有效。

［1］ Shen G Y，Xiao Z H，Zhang W，et al.Nonlinear behavior analysis of a rotor supported on fluid-film bearing［J］.Journal of Vibration and Acousti-cs，2006，128：35-40.

［2］徐小峰，张 文.一种非稳态油膜力模型下刚性转子的分岔和混沌特性［J］.振动工程学报，2000，13（2）：247-253.

［3］Das A S，Nighil M C，Dutt J K.Vibration control and sta-bility analysis of rotor-shaft system with electromagn-eticexciters［J］.Mechanism and Machine Theory，2008，43：1295-1316.

［4］ Fan C C，Pan M C.Fluid-induced instability elimination of rotorbearing system with an electro-magnetic exciter［J］.International Journal of Mechanical Sciences，2010，52：581-589.

［5］Yong K.Theory of intelligent neural network［M］.D.P.R.Korea Pyongyang University of Science Press：Kim Yong Hi，2009.

［6］王耀南.计算智能信息处理技术及其应用［J］.长沙：湖南大学出版社，1999.

［7］Ramesh M，Narayanan S.Chaos control of Bonhoeffer-Van der Pol oscillator using neural networks［J］.Chaos，Solitons and Fractals，2001，12：2395-2405.

［8］谭 文，王 耀.非线性系统混沌运动的神经网络控制［J］.物理学报，2002，51（11）：2463-2466.

［9］ Qin W Y，Yang Y F，Zhang J F.Controlling the chaotic response to a prospective externalsignalusing backpropagation neural networks［J］.Nonlinear Analysis：Real World Application，2009，10：2985-2989.

［10］ Pyragas K.Continuous control of chaos by self-controlling feedback［J］.Phys Lett A，1992，170：421-428.

［11］ Hiroyuki N J.On analytical properties of delayed feedback control of chaos［J］.Phys Lett A，1997，232：207-210.

［12］黄文虎，夏松波，焦映厚，著.旋转机械非线性动力学设计基础理论与方法［J］.北京：科学出版社，2006.

［13］ Adiletta G，Guido A R，Rossi C.Chaotic motions of a rigid rotor in short journal bearings［J］.Nonlinear Dynamics，1996，10：251-269.