进动分解及其在转子动平衡中的应用

雷文平，韩 捷，陈 宏，巩晓赟

（1.郑州大学 振动工程研究所，郑州 450001；2.郑州大学 化工与能源学院，郑州 450001）

影响系数法作为一种主要的转子动平衡方法在工业现场使用广泛［1］.由于影响系数法建立于线性假设的基础之上，在应用过程中仍然存在很多不足之处［2-3］.特别地，当转子支撑的各向刚度存在明显差异时，传统的基于影响系数法的平衡效果不稳定，会受传感器影响，经常发生以下现象：① 传感器安装方向不一样，动平衡效果不一样；② 利用某些特定方向上的传感器会导致最后计算的配重大到无法实施。针对这一问题，屈梁生院士提出了全息动平衡方法［2］，采用双传感器的信息融合方法克服了单传感器的片面性，得到了较好的应用.然而全息动平衡技术建立在模态平衡法的基础上，采用力和力偶分解的原理进行平衡，因而只能进行低阶振型的平衡，对于超二临界的转子的平衡则不适用。本文在分析传统影响系数法的弊端的基础上，采用双传感器信息融合技术，并采用正进动来代替传统不平衡响应进行影响系数法改进，取得了良好的效果。

1 传统影响系数法的弊端

影响系数平衡法涉及以下方程［3］：

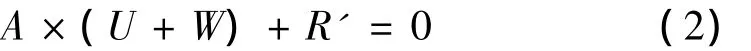
联立方程（1）和方程（2），便可以求出A和U。因此，不平衡响应（R和R'）的准确性决定了平衡结果的准确性。传统方法不平衡响应是采用单方向传感器测量的，对于各向异性转子来说，从同一截面x，y方向传感器测得的不平衡响应往往并不相同。从图1中可以明显看出，x方向响应幅值要大于y方向，尽管x，y方向传感器夹角为90°，其相位差并不为90°。

图1 传感器安装方向与不平衡响应的对应关系Fig.1 The relation between installed direction of sensor and unbalance response

2 工频轨迹的进动分解

按图1的传感器器安装方式，设某测点x，y方向的工频振动分别为：

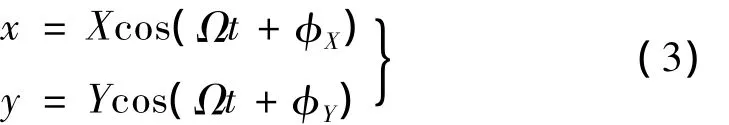
式中，X，Y分别表示在x，y方向检测到的信号幅值；φX、φY表示x，y方向的相位角，Ω表示转速。定义：

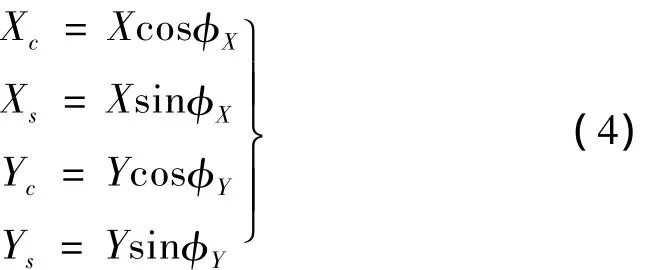
则式（3）可以写成：

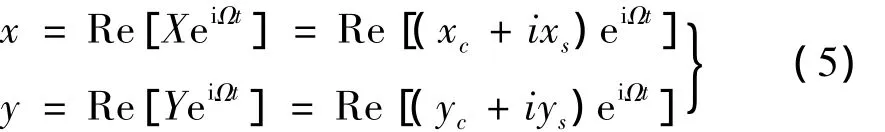
将式（5）消去时间变量t可以得到一个椭圆轨迹，得到：

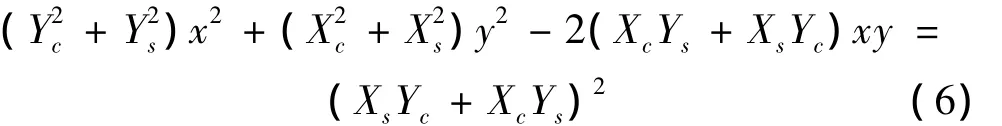
在运动学上，转子沿椭圆轨迹的运动可看作是两个频率相同而进动方向相反的圆轨迹分运动的合成［4-6］：

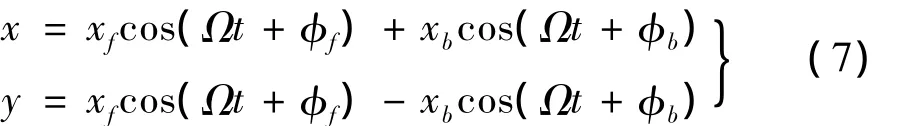
用复平面上的点r（r=x+iy）表示椭圆上的一点，即：

式中：rfc和rbs分别为rf的实部和虚部，rbc和rbs分别为rb的实部和虚部，令φf和φb分别为正进动圆和反进动圆的初始相位角，Rf和Rb分别为rf和rb的模，有：

所以：

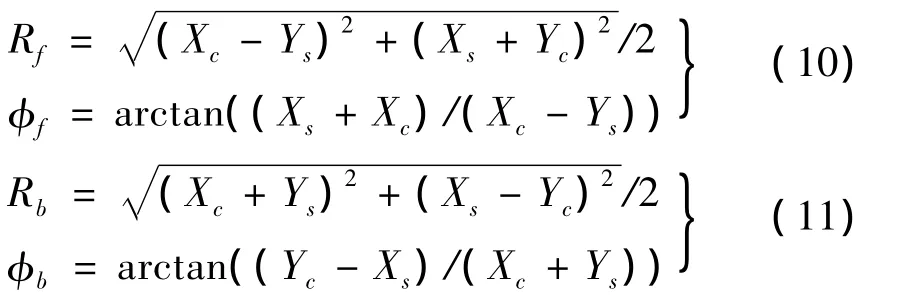
当Rf＞Rb时，转子为正进动，Rf＜Rb时，转子为反进动。当Rf=Rb时转子的涡动轨迹为一直线。椭圆的长半轴RL和短半轴RS与两个进动圆的关系为：

椭圆轨迹的偏心率为：

3 改进影响系数法

由文献［3］可知：转子运转过程中一般为同步正进动，即以正进动分量Rf为主。由式（12）、式（13）可知，随椭圆轨迹的偏心率e的减小，反进动分量Rb越来越小，当e减至0时，Rb也减小为0，可见反进动分量与转子不平衡不存在必然的联系。实际上当转子振动情况比较复杂、轨迹偏心率较大时，由于反进动的存在给转子失衡量的估计带来了不可忽略的干扰，造成了平衡的效率降低［7］。

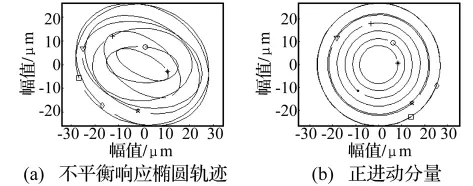
图2 单圆盘转子在不同的不平衡力的作用下的轨迹和正进动分量Fig.2 Whirl orbit and forward precession component of rotor excited by different unbalance force

实验中，在单圆盘转子（具有一定的初始不平衡量）上施加质量为 2 g，角度分别为 0°，45°，90°，135°，180°，225°，270°，315°的不平衡质量后，转子的涡动轨迹和正进动圆轨迹如图2所示。相对于图2（a）中的涡动轨迹来说，正进动分量图2（b）更好地体现了不平衡状态，正进动圆的半径反映了不平衡量的大小，正进动角度反映了不平衡量的相位。

因此，改进影响系数法的基本思路是：将工频正进动圆的幅值Rf作为不平衡响应幅值，正进动相位角φf作为不平衡响应的相位，即新的不平衡响应Rf＜φf成为正进动不平衡响应（Forward Precession Unbalance Response，FPUR），结合影响系数法采用计算机辅助型平衡过程来完成平衡。

4 数值模拟

转子-轴承系统的有限元模型由方程（14）表示［1］：

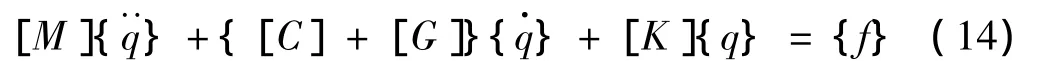
其中：［M］，［C］，［G］，［K］分别表示质量阵、阻尼阵、陀螺阵和刚度阵，Ω表示主轴的旋转角速度，假定转子绕Z轴旋转，{q}=（rX，rY，θX，θY）T表示各个有限元节点的解，rX，rY分别表示X，Y方向的位移，θX，θY为绕X，Y轴的角位移，{f}={u}eiΩt代表不平衡力。在ANSYS中，可以用COMIN214来模拟轴承，它可以模拟各向异性的轴承.轴的模拟采用BEAM188单元，圆盘的模拟采用MASS21单元.建立模型后，可通过谐响应分析解方程（14）求稳态涡动响应［8］。

本文建立的转子-轴承模型如图3所示，盘P1-P5的直径转动惯量和极转动惯量分别为1.54×10-4kg·m2和2.94 ×10-4kg·m2。质量为0.783 kg。轴承特性：kxx=2.63e+6 N·m-1，kyy=1.315e+6 N·m-1，kxy=kyx=-2.63e+5 N·m-1，由于不考虑阻尼影响，cxx=cyy=cxy=0。该模型的主要参数还包括：主轴总长度0.36 m，半径为 0.004 8 m，杨氏模量 2.1e11 N·m-3，泊松比为 0.3，密度为 7 800 kg·m-3。转子的第一，二阶临界转速分别为1 921和7 238 r/min，对应的反进动临界转速分别为1 883和6 472 r/min。沿轴的方向，从左到右，均匀分布13个节点，节点号分别为 S1，S2，…，S13.节点号在图3 中标识.在节点3，5，7，9，11处建立圆盘.为了验证改进方法的动平衡效果，设计了两组实验，分别采用了不同的初始不平衡分布和不同的平衡转速进行转子动平衡的数值模拟，初始不平衡量的分布情况如表1所示，实验1和2的平衡转速分别选为1 200、3 600 r/min，前者低于第一临界转速，后者位于第一、二临界转速之间。

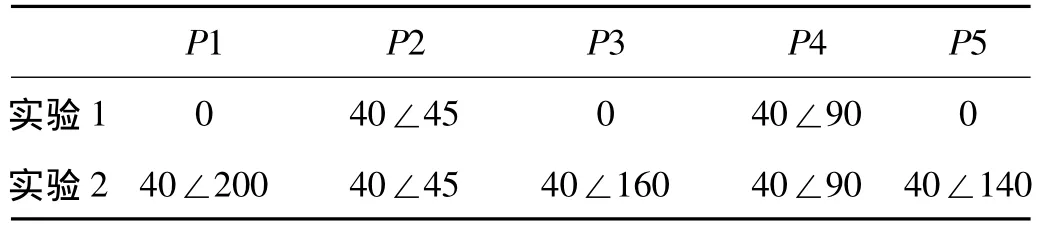
表1 2组实验对应的初始不平衡量（单位：g∠°）Tab.1 Initial unbalance distribution（unit：g∠°）

实验1中典型的平衡数据如表2所示，结果显示改进方法与X，Y单方向计算结果相同，即当校正平面和不平衡平面正好相同的情况下改进方法与传统方法具有相同的结果，同时作者分别用转速2 400，3 600，4 800，6 000和7 200转进行实验，结论均一致.因为采用传统方法时X，Y方向均得出了完全精确的结果，所以改进方法在这种情况下与传统方法是兼容的。

在实验2中，由于平衡分布较为复杂，校正平面仍然选为P2和P4，从表2中可以看出此时，采用X，Y单方向的平衡计算结果不再一致了，显然实验2更接近现场转子的真实情况。由于，改进方法融合了X，Y两个方向的结果。因此从平衡后的结果（表3和图4）看，改进方法优于传统方法。

表2 实验1数据（转速：1 200 r/min）Tab.2 Experimental data 1（rotating speed：1200 r/min）

表3 实验2数据（转速：3 600 r/min）Tab.3 Experimental data 2（rotating speed：3 600 r/min）

图4 平衡前后不同节点振动对比Fig.4 Whirl response before and after balancing

5 实验研究

为了验证改进方法的平衡效果，在BENTLY转子实验台上进行了实验。图5为转子实验台及传感器安装示意图，转子由滑动轴承支撑，支撑的各向刚度存在一定的差异，转子通过挠性联轴节与电机相联，两个圆盘上各均匀分布16个加重小螺纹孔，两个孔之间的夹角为22.5°。沿轴从左至右方向上，两个圆盘分别为P1和P2，在靠近左右连个轴承附近分别安装两对互相垂直的电涡流传感器，分别为S1X，S1Y和S2X，S2Y，K φ为键相传感器。转子第一阶临界转速为1 180 r/min，实验时平衡转速选在1 600 r/min。

表4为双面平衡的实验数据，由于轴承的各向刚度的差异，X，Y方向响应（振幅）差别较大，因而最后的平衡结果差别也比较大，尤其是采用X方向的平衡效果很差，平衡后的残余振动最大，相比较而言，改进方法具有结果客观唯一，其平衡效果最好。

图5 转子实验台模型Fig.5 Illustration of rotor test fig

表4 转子实验台实验数据（转速：1 600 r/min）Tab.4 Experimental data using rotor test fig（rotating speed：1 600 r/min）

6 结论

通过分析和实验研究，得到如下结论：

（1）转子的工频椭圆轨迹可以分解为两个频率相同但旋转方向相反的圆轨迹，分别为正进动圆和反进动圆，工业现场的失衡转子一般处于稳态的同步正进动状态，即正进动分量占主导因素，正进动圆较好地反映了转子的不平衡状态，其半径反映了不平衡量的大小，其初始相位角反映了不平衡量的相位，而反进动分量与转子不平衡不存在直接和必然的联系。

（2）提出一种基于影响系数法的改进平衡方法，该方法采用正进动分量代替传统方法的不平衡响应进行转子平衡。数值模拟结果表明，在忽略任何非线性干扰和测量误差情况下，传统方法和改进方法结果趋于一致，具有兼容性。由于改进方法结合了两个方向传感器的信号，克服传统平衡方法中平衡效果受传感器安装方向影响的弊端，在实际转子平衡中结果客观，唯一，效果更好。具有较好地工程应用价值。

［1］ Kang Y，Lin T W，Chang Y J，et al.Optimal balancing of flexible rotors by minimizing the condition number of influence coefficients［J］.Mechanism and Machine Theory，Mechanism and Machine Theory，2007，43（7）：891-908.

［2］屈梁生，邱 海，徐光华.全息动平衡技术：原理与实践［J］.中国机械工程，1998，9（1）：60-63.

［3］周仁睦.转子动平衡-原理、方法与标准化学工业出版社［M］.北京：化学工业出版社，1992.

［4］钟一谔，何衍宗，王 正，等.转子动力学［M］.北京：清华大学出版社，1987.

［5］韩 捷，石来德.全矢谱技术及工程应用［M］.北京：机械工业出版社，2008.

［6］陈先利，韩 捷.基于全矢谱的旋转机械回转相位及应用研究［J］.机械科学和技术，2008，27（4）：515-519.

［7］廖与禾，郎根峰，屈梁生.平衡目标选择与全息动平衡法的改进研究［J］.热能与动力工程，2008，23（4）：382-386.

［8］ Release 12.0 documentation for ANSYS［M］.SAS IP，Inc.，USA，2009.