基于滚珠丝杠副流畅性的滚珠返向器型线优化设计

姜洪奎，宋现春，李保民，唐文成，朱继生，荣柏松

（1.山东建筑大学 机电学院，济南 250101；2.山东博特精工股份有限公司，山东 济宁 272071）

滚珠丝杠副返向器的滚道型线是影响滚珠丝杠副性能的关键参数。滚珠在循环通过返向器过程中，其受力状态在预紧状态和自由状态之间不断发生突变。由于滚珠在整体滚珠丝杠副中起到动力传输作用，所以滚珠在返向器内的运动循环过程直接影响着整个滚珠丝杠副进给系统的动力学性能。滚珠丝杠副返向器的型线不仅是影响滚珠丝杠副低频噪声的主要因素，也是影响滚珠丝杠副寿命的主要因素［1－3］。

目前广泛应用于高速滚珠丝杠副滚珠返向器类型为端塞式滚珠返向器，围绕其结构形式以及对滚珠丝杠副动力学影响国内外学者已做了大量的有益工作［4－6］：① 返向器的弹性联接。通过改进返向器与螺母之间的弹性联接减少滚珠与返向器之间的冲击达到降低噪声的目的。② 滚珠与返向器的碰撞接触仿真［7－8］。采用多体动力学软件ADAMS对单个滚珠与返向器之间的接触进行动力学仿真。然而，以上述工作存在两方面的问题：① 对于滚珠与滚珠返向器之间的碰撞的研究对象，只限于单个滚珠，而事实上滚珠在返向器内循环运动时，一般排列成滚珠链的形式，因此所建立的模型不能全面反映滚珠在返向器内的循环运动状态。② 返向器滚道型线的设计方法。目前国内返向器的设计一般采用苏联的标准和经验设计，而随着滚珠丝杠副进给速度的提高，越来越需要新的设计方法和理论对返向器的滚道型线进一步优化设计。

本文在滚珠丝杠副运行过程中滚珠与返向器内碰撞接触过程的分析基础上，建立了滚珠与返向器之间的碰撞接触模型，提出了一种滚珠返向器双圆弧滚道型线和优化设计方法，提高了滚珠丝杠副的摩擦力矩的平稳性和效率，为高速滚珠丝杠副的研发提供了理论依据和设计方法，促进了我国装备制造业的发展。

1 滚珠与滚道之间接触碰撞分析

滚珠丝杠副在轴向载荷的作用下，中间元件滚珠分别与螺母、丝杠滚道面接触，以传递载荷，并产生相应的接触变形。研究表明，在滚珠丝杠副平稳运行过程中，滚珠往往在返向器滚道和贯穿孔内排列成首尾相连的滚珠链；滚珠与返向器之间的碰撞是引发滚珠丝杠副进给系统产生低频振动和噪声的主要机制。因此，优化设计返向器滚道型线，需要分析滚道型线对滚珠与返向器之间的碰撞力和循环时产生的阻力的影响。

1.1 滚珠与返向器滚道之间的碰撞接触模型

滚珠进入返向器的过程可以等效为球与圆管内表面之间的碰撞接触模型。在滚珠丝杠副的装配过程中，为了减少滚珠与返向器之间的碰撞，往往要在返向器和螺母之间安装弹性连接件，因此滚珠与循环装置之间的力学模型可以等效为如图1所示的模型。图1中R1为钢球半径，r1和r2分别为返向器圆形截面半径和滚道型线轨迹的曲率半径。

根据赫兹接触理论，接触力与接触刚度之间的关系为：

其中：δ为法向变形量，kh为赫兹接触刚度。

图1 滚珠与返向器碰撞图示和等效模型Fig.1 The contact between ball，returner and the equivalent model

赫兹接触刚度kh可以由以下公式推导得出：

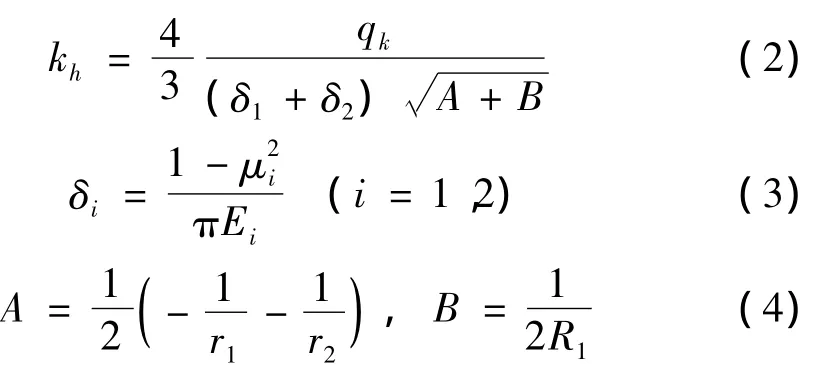
其中：E1，E2，μ1和μ2分别为钢球和返向器两种材料的弹性模量和泊松比。qk为A/B的比值［9］。

考虑到赫兹接触力同时也反作用于钢球，因此根据牛顿第二定律：

考虑到钢球加速度、返向器以及碰撞接触变形区域的相互关系，可以得出：

将等式（1）代入等式（5）可得：

其中，

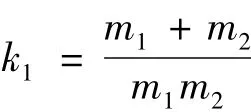
一般情况下，返向器是通过锁紧垫片与螺母之间相互锁紧，所以两者之间的连接刚度较大，因此可以认为ky=∞。滚珠与返向器之间的碰撞过程中，当滚珠速度等于零时，加速度达到最大，也就是返向器发生最大变形量的位置，因此：

将等式（8）代入公式（1），可以得出返向器发生最大变形δm2和同时产生的最大碰撞力Fm2。

由式（2）－式（4）和式（11）可得钢球和返向器之间的碰撞力与滚道型线半径的关系为，

1.2 滚珠链循环力学模型

根据文献［2］，在滚珠丝杠副运行过程中，由于滚珠进入返向器时脱离了螺母滚道的预紧力作用，滚珠之间相互推挤，在返向器内排列成首尾相连的滚珠链。因此滚珠丝杠副平稳运行时返向器内滚珠之间的受力模型简化为图2所示。图2中由于滚珠与滚道之间的几何间隙以及阻力的存在，滚珠1、滚珠3的中心位于半径为r2+e的型线圆上，而滚珠2位于半径r2－e的型线圆上，其中r2为滚道型线半径、e为滚珠半径与滚道截面半径之差。α1、α2、α3、α4分别为滚珠受到的作用力与滚珠中心轨迹水平方向的夹角，由几何相对关系可以计算得出入射角；N1、N2、N3为返向器对滚珠的作用力，FN1、FN2、FN3、F'N1、F'N2、F'N3为滚珠之间的相互接触力，Ff1、Ff2、Ff3为滚珠与返向器之间的摩擦力。

假设滚珠丝杠副平稳运行过程中，滚珠之间的相对位置不变，且沿着滚道型线中心的角速度为ω，以返向器内的滚珠为研究对象，分别建立各个滚珠的力学平衡方程。

图2 滚珠链与返向器碰撞等效模型Fig.1 The contact between ball and returner and the equivalent model

由球1的受力平衡方程可得，

其中，

同理得滚珠2的力学平衡方程：

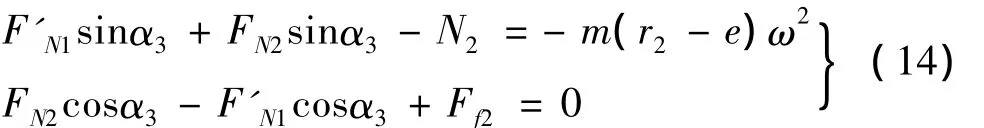
其中：

滚珠3的力学平衡方程：

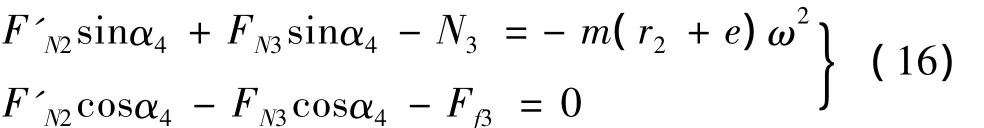
其中：

为描述滚珠在返向滚道内的传动效率，本文做如下定义：设滚珠链初始滚珠受到的有效驱动力与有效阻力的比值为驱阻比η，则如图2所示由球1、球2、球3组成的滚珠链的驱阻比为：

1.3 新型滚道型线

由公式（11）可知滚珠与返向器之间的碰撞力大小与滚道型线半径成反比，同时由式（12）～式（18）可知，滚珠链驱动效率与滚道型线相关。因此对于单圆弧滚道型线，要降低碰撞力的大小必须增大滚道型线的半径。这样必须加大返向器的尺寸，同时也增加了滚道长度和滚珠在返向滚道内的个数。而滚珠数目的增多势必会降低滚珠链的流动效率，增大了滚珠链流动阻力。为了解决这一矛盾，本文提出了双圆弧滚道型线形式如图3。

图3 双圆弧滚道型线示意图Fig.3 The double arc profile of the passage in the ball returner

2 优化方法与分析

2.1 目标函数

优化目的是通过调整滚珠返向器滚道型线的参数，改善滚珠在返向器内的循环特性，降低整体滚珠丝杠副的振动和噪声，提高机床进给系统的动力学性能，因此，选择滚珠返向器流畅性的评价指标——驱阻比和滚珠与返向器碰撞力作为目标函数。由式（12）可知，滚道型线半径越大，则滚珠与返向器之间的碰撞力越小，为了简化计算设目标函数如下：

2.2 设计变量

2.3 约束

循环链滚珠间隙过小将导致循环时滚珠因“挤死”发生卡滞现象，滚珠间隙过大将增大滚珠间的冲击摩擦，使滚珠循环损耗增大并产生较大噪声。因此要确保返向器型线的长度，使得循环链滚珠间隙在0.6～0.8倍滚珠直径范围内［10］。

s0.6为循环滚珠链间隙为0.6倍滚珠直径的滚道型线长度，s0.8为循环滚珠链间隙为0.8倍滚珠直径的滚道型线长度。

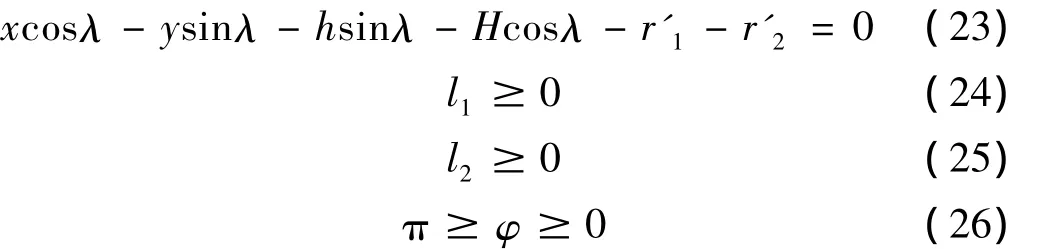
2.4 优化方法和程序设计

遗传算法是以自然选择和遗传理论为基础，将生物进化过程中适者生存与群体内部染色体的随机信息交换机制相结合的高效全局寻优搜索算法。与传统的优化方法相比，遗传算法不需要求出目标函数的导数信息；而是采用概率的、不确定状态的转移规则；尤其适用于较难获得目标函数导数值的优化问题，如带接触的含多构件的装配体优化问题［11］。

图4 优化程序路线Fig.4 The flow chats of the optimal program

根据本文提出优化数学模型的特点，选择遗传算法对目标函数进行求解。具体优化方法的过程见图4。首先将设计变量初始化，选取Matlab中的GA函数作为优化工具，对目标函数进行优化计算。对求得的设计方案进行驱阻比的计算，驱阻比根据公式（12）～式（18）所建立的力学理论模型编制程序计算。通过比较获得最终的最优方案。

3 新型端塞式滚珠返向器优化设计

3.1 返向器结构参数

选取某滚珠丝杠副的端塞式滚珠返向器作为优化设计对象，其滚珠半径rb为2.976 5 mm，螺旋升角λ为9.05°，滚道型线入口点与出口点的水平相对位置H为19.52 mm，竖直相对位置h为6.98 mm，滚道型线的长度上限s0.8为 25.08 mm，下限s0.6为 24.56 mm。设定返向器滚道型线参数初始值如表1所示，利用本文提出的优化方法，确定滚珠返向器滚道型线的最优方案，优化前后的滚珠副滚珠返向器的形状对比如图5所示。由图5可以看出，由于优化后的滚道采用了双圆弧型线，其开口和出口位置的曲率变化相对于优化前更加平滑。

表1 滚珠返向器滚道型线的结构参数Tab.1 Parameters of the passage profile in ball returner

图5 优化前后滚珠返向器的模型对比Fig.5 Comparison among ball returners before and after optimization

3.2 方案分析和论证

为了比较滚珠返向器的设计参数优化前后对整体滚珠丝杠副的性能的影响，本文按照优化前后滚珠返向器的结构参数，利用Pro/Engineer软件建立了滚珠丝杠副的CAD模型，并通过接口导入多体动力学软件ADAMS。根据滚珠丝杠副内部构件之间的运动关系，本文建立了如图6所示的多体动力学仿真模型。如图6所示，两个返向器与螺母固定连接，滚珠之间、滚珠与螺母以及滚珠与丝杠轴之间施加solid to solid接触副，螺母与大地之间施加沿轴向的移动副，所建多体动力学模型的拓扑结构图如图7所示。

图7 滚珠丝杠副的拓扑结构Fig.7 The topography of multi-body dynamical model of the ball screw mechanism

为了减少仿真计算中误差累积，设定滚珠丝杠副的丝杠转速在0 s～0.01 s内保持静止，在0.01 s～0.02 s内加速到3 600 r/min，在 0.02 s～0.04 s内保持固定转速3 600r/min，在0.04 s～0.05 s内减速到 0 r/min。在上述工况下，滚珠返向器优化前后，滚珠丝杠副摩擦力矩变化情况对比如图8所示。安装有滚道型线的，优化后的整体滚珠丝杠副的摩擦力矩变化情况如图8（b）。

设计参数优化前后整体滚珠丝杠副摩擦力矩变化参数的比较如表2所示。

图8 优化前后滚珠丝杠副摩擦力矩的对比Fig.8 Comparison friction torque of the ball screw mechanism before and after optimization

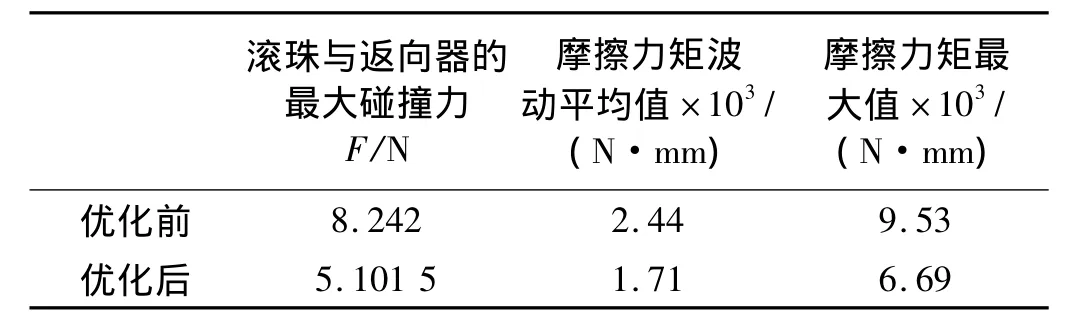
表2 优化前后滚珠丝杠副的摩擦力矩比较Tab.2 Comparison of the ball screw mechanism friction torque before and after optimization

4 结论

（1）运用赫兹接触理论，并考虑滚道型线曲率半径的影响，分析了滚珠与返向器之间的碰撞力与滚道型线几何参数的关系，在此基础上，提出了评价滚珠循环返向的流畅性技术指标——驱阻比。

（2）对目前滚珠返向器滚道型线做出了改进，提出了一种由两相切圆弧组成的滚珠返向器滚道型线，并在滚珠循环返向流畅性的分析基础上，提出了以驱阻比和碰撞为优化设计目标，以双圆弧半径和相对厚度为优化设计变量的滚道型线形状优化方法。

（3）应用该优化模型，对某滚珠返向器滚道进行了优化计算和分析，使得滚珠与返向器之间的接触力降低了38.1%，滚珠丝杠副摩擦力矩的最大值降低了29.8%，摩擦力矩波动平均值降低了29.9%，成功地实现滚珠返向器滚道型线的优化设计，为滚珠返向器的设计和开发提供了可靠的理论依据。

［1］Ninomiya M，Miyaguchi K.Recent technical trends in ball screws［J］.NSK Tech Journal：Motion Control，1998，664：1－3.

［2］Claudio B，Luca L.A general elastic-plastic approach to impact analysis for stress state limit evaluation in ball screw Bearings return system［J］.International Journal of Impact Engineering，2007，34（7）：1272 －1285.

［3］Jui P H，Wu J S，Chiu J Y.Impact failure analysis of recirculating mechanism in ball screw［J］.Engineering Failure Analysis，2004，11：561 －573.

［4］Jiang H K，Song X C，Zhang Z Y.Dynamics analysis and simulation of re-circulating mechanism in ball screw［C］.Proceedings of the 12th International Manufacturing Conference，Xi’an，China，2006：223 －227.

［5］姜洪奎，宋现春.滚珠丝杠副滚珠循环系统的动力学研究和仿真［J］.振动与冲击，2007，26（3）：107－111.

［6］HIWIN.Technical strategy for high-speed ball screw units［J］.Manufacturing Technology ＆ Machine Tool，2003，12：87－88.

［7］程光仁，施祖康，张超鹏.滚珠螺旋传动设计基础［M］.北京：机械工业出版社，1987.

［8］ Song X C， Liu J， Wang Z T，et al. Research and development of test system of combination property of highspeed ball screw unit［J］.Tool Engineering，2005，3：34－36.

［9］Goldsmith W.Impact：the Theory and Physical Behavior of Colliding Solids［M］.London：Edward Arnold Ltd，1960.

［10］饶振纲，王勇卫.滚珠丝杠副及自锁装置［M］.北京：国防工业出版社，1990.

［11］席裕庚，柴天佑，恽为民.遗传算法综述［J］.控制理论与应用，1996，13（6）：697－708.