基于高斯曲率模态差的T梁结构二维损伤识别研究

韩 西，李庆达，钟 厉，杨 科

(1.重庆交通大学土木建筑学院，重庆 400074;2.重庆交通大学 机电与汽车工程学院，重庆 400074)

基于高斯曲率模态差的T梁结构二维损伤识别研究

韩 西1，李庆达1，钟 厉2，杨 科1

(1.重庆交通大学土木建筑学院，重庆 400074;2.重庆交通大学 机电与汽车工程学院，重庆 400074)

曲率模态是识别损伤的敏感指标，基于曲率模态的损伤识别研究大多局限于一维结构。为将曲率模态的损伤识别方法推广到二维结构，提出了基于高斯曲率模态的损伤识别方法，综合考虑二维结构的加速度振型曲面在纵向和横向上的弯曲程度，通过计算结构损伤前后加速度振型的高斯曲率差来判断结构损伤的位置。T梁组合结构的模态试验及试验分析结果验证了该方法的可行性。

高斯曲率;T梁组合结构;损伤识别;二维识别

随着经济的飞速发展，桥梁结构的正常运营日趋重要，同样也关系人们的人身安全。对于桥梁结构的振动，由模态分析理论可知，振动系统的特性可以用固有频率，振型，阻尼等模态参数来描述。由于结构发生损伤将会引起结构振动特性的变化，因此我们可以通过模态分析所得到的模态参数的改变来判断结构损伤和识别损伤位置，归结为数学上的反演问题。

固有频率是基于模态参数的最早的损伤识别方法之一［1］。固有频率虽然容易获得，且识别精度高，但是固有频率是结构的整体属性，不同位置或者不同程度的损伤可能会造成固有频率相同的改变量，有时结构的微小损伤对固有频率的影响不显著。因此，研究表明固有频率一般不作为识别损伤的指标。随后，基于固有频率和模态振型所构建的损伤指标，如柔度矩阵［2］、模态应变能［3］等，均能有效地识别结构的损伤位置。自从Pandey，等［4］提出了曲率模态的概念以后，由于该指标对于损伤的高灵敏性，受到众多学者的极大关注。在胡业平，等［5］的研究中，构建了曲率模态差指标，根据结构损伤前后绝对曲率差曲线定位损伤。

对于板类结构，其损伤的定位需要二维识别，高斯曲率模态差方法对于定位板类结构的损伤和识别损伤程度都是行之有效的方法［6］。笔者在文献［6］提出的高斯曲率模态差的基础上，进一步研究改善措施，实现了二维损伤识别，通过T梁组合结构的试验分析结果验证了该方法的有效性。

1 高斯曲率模态差原理

结构的振动控制方程:

大量研究证明，通过位移振型构建的众多损伤指标，均能有效识别结构的损伤。然而从式(8)看出，加速度频响函数与位移频响函数仅相差一个系数 -1/ω2，因此可望从加速度振型数据中识别结构的损伤。并且，结构的加速度响应也相对容易测得，加速度振型通过对加速度频响函数拟合得到。

二维结构的模态振型在空间上表现为曲面的形式，设二维结构的某阶振型如图1。则振型曲面上任一点 Q［x，y，z(x，y)］的两个主曲率为 k1和 k2，则该点的高斯曲率表示为［8］:

图1 结构的振型曲面Fig.1 Mode shape of structure

实际应用中，利用差分法计算振型曲面上某一点对该位置处x，y方向的各阶偏导数，代入式(9)即可计算出振型曲面在该位置的高斯曲率，通过损伤前后高斯曲率模态差来识别损伤位置。

2 参数的计算与选取

2.1 曲率的计算

基于曲率模态的损伤识别方法，在实际结构的模态分析中，测点布置得越稀疏，模态振型数据量越少，由此产生的曲率模态计算误差就越大，误差甚至有可能大到掩盖损伤，使识别方法失效。因此，笔者在计算T梁组合结构的高斯模态曲率之前，先通过3次样条插值方法对各阶模态振型数据进二维插值处理，旨在减小由于测点不足造成的计算误差。

2.2 模态阶数的选取

目前曲率模态的损伤识别方法，都是在某一阶曲率模态的计算中识别损伤，但是由于模态振型中节点或节线的存在，位于节点或节线处的损伤很有可能在这一阶模态振型中被掩盖。因此，笔者综合考虑了前3阶加速度振型的高斯曲率差值来进行损伤识别。

若第i阶的高斯曲率模态矩阵为Ki，定义由结构的前3阶加速度振型构成的高斯曲率模态差矩阵为:

式中:Kui和Kdi分别为结构损伤前后的第i阶高斯曲率模态矩阵;ai为第i阶模态的权重系数。

通常在结构的振动中，低阶模态起主导作用，且低阶模态的测试精度容易保证。因此，文中取a1=0.4，a2=0.35，a3=0.25。

3 模型试验

3.1 试验方案

在实验室中，用C30混凝土浇筑钢筋混凝土组合T梁模型进行试验研究。全梁长 5.3 m，宽1.5 m，计算跨径为5.1 m，两端简支放置。试验梁的截面尺寸及配筋情况见图2和图3。

图2 试验模型Fig.2 Experimental model

图3 配筋图Fig.3 Reinforcement plans

利用LMS动态测试系统进行信号采集，加速度传感器的布置如图4。

图4 测点布置Fig.4 Arrangement of measuring sensors

在1号梁右侧的1/4跨附近用力锤进行竖向锤击激励。固定敲击点，移动传感器，获得7排17列共119个测点的加速度(响应)信号。采样频率为2 048 Hz，对力信号加Hanning窗，对加速度(响应)信号加指数窗，并且对信号进行5次平均以消除噪声和人为因素造成的影响。最后通过LMS动态测试系统的模态分析模块对加速度频响曲线拟合得到结构的模态参数，最后由损伤前后的加速度振型数据计算得到的高斯曲率模态差识别损伤。

3.2 损伤工况

得到完好结构的模态参数后，利用螺旋千斤顶加载系统对结构的跨中位置加载，使跨中位置及其附近产生不同数量和不同程度的裂缝。笔者考虑了3种损伤工况(表1)，由结构跨中位置附近裂缝的不同发展情况设置损伤工况，各个损伤工况模拟了T梁组合结构在跨中位置处的不同损伤程度。

表1 损伤工况Table 1 Damage case

笔者通过不同的裂缝数量和宽带模拟了结构不同程度的损伤。从表2中可以看出，结构存在损伤时，其固有频率降低了。

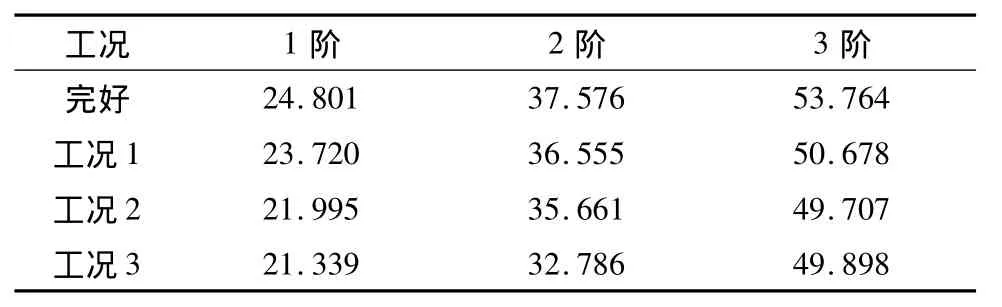
表2 T梁结构各工况的固有频率Table 2 Natural frequency of T-beam in each case /Hz

3.3 损伤识别结果与分析

通过试验获得T梁组合结构的完好和各损伤工况的模态参数后，在MATLAB中编制程序，由式(9)计算出各工况的各阶加速度振型的高斯曲率，最终由式(10)计算高斯曲率模态差矩阵。各工况的损伤识别结果如图5，从竖向的柱状图中可以识别损伤。图中柱状图的大小表示结构损伤前后振型曲面变化的大小，柱状图越大的位置，即越可能存在损伤的位置。

图5 工况1～工况3高斯曲率模态差值Fig.5 Gaussian curvature mode difference of case 1 －3

从工况1的识别结果中看出，如开裂0.1 mm的微小损伤，笔者提出的方法仍然能正确识别出T梁组合结构在跨中附近的损伤，高斯曲率模态差最大值为 2.2E-10。

在增大损伤程度后，最大裂缝宽度为0.2 mm，工况2的识别结果也正确识别了结构的损伤位置，高斯曲率模态差最大值为2.4E-10。随着损伤程度的增加，各阶模态振型在该损伤位置处的改变量增大，得到的高斯曲率模态差值也随之增大。

工况3中进一步模拟结构的裂缝数量和损伤程度继续增加，识别结果也正确显示了结构的损伤信息，并且该工况下识别出的裂缝数量较前两个工况多。此时的高斯曲率模态差最大值增大到了6.45E-10。

4 结论

基于高斯曲率模态差的损伤识别方法，适合二维结构的损伤定位，以T梁组合结构的试验研究验证了该方法的可行性，得出以下结论:

1)结构发生损伤后将引起该损伤处的模态振型改变，笔者提出高斯曲率模态差值损伤指标，将曲率模态的损伤识别方法从一维结构推广到二维结构。

2)通过试验分析结果表明，T梁组合结构的高斯曲率模态差可识别损伤。因此该方法对于二维结构的损伤定位是可行并且有效的。

3)从识别结果中看出，如0.1mm的微小损伤仍然可以正确识别，表明基于高斯曲率模态的损伤识别方法对识别损伤是敏感的。

4)随着损伤程度的增加，高斯曲率模态差最大值也随之增加。结构发生损伤后，非线性因素使结构的振动特性更为复杂。本文的方法尚未能定量描述高斯曲率模态差值与结构损伤程度的关系。

［1］高维成，刘伟，邹经湘.基于结构振动参数变化的损伤探测方法综述［J］.振动与冲击，2004，23(4):1-7.

Gao Weicheng，Liu Wei，Zou Jingxiang.Damage detecyion methods based on changes of vibration parameters:a summary review［J］.Journal of Vibration and Shock，2004，23(4):1-7.

［2］Pandey A K，Biswas M.Damage detection in structures using changes in flexibility［J］.Journal of Sound and Vibration，1994，169(1):3-17.

［3］Cornwell P，Doebling S W，Farrar C R.Application of the strain energy damage detection method to plate-like structures［J］.Journal of Sound and Vibration，1999，224(2):359-374.

［4］Pandey A K，Biswas M，Samman M M.Damage detection from changes in curvature mode shapes［J］.Journal of Sound and Vibration，1991，145(2):321-332.

［5］胡业平，张成海，屠义强.基于曲率模态的结构损伤定位［J］.解放军理工大学学报:自然科学版，2009，10(增刊1):57-63.

Hu Yeping，Zhang Chenghai，Tu Yiqiang.Curvature mode-based structure damage localization［J］.Journal of PLA University of Science and Technology:Natural Science，2009，10(supp1):57-63.

［6］何钦象，杨智春，姜峰，等.薄板损伤检测的高斯曲率模态差方法［J］.振动与冲击，2010，29(7):112-115.

He Qinxiang，Yang Zhichun，Jiang Feng，et al.Damage detection for an elastic thin plate based on Gauss curvature modal difference［J］.Journal of Vibration and Shock，2010，29(7):112-115.

［7］ 李德葆，陆秋海.实验模态分析及其应用［M］.北京:科学出版社，2001:63-67.

［8］ 周振荣，杨文茂，郑高峰，等.微分几何［M］.武汉:武汉大学出版社，2008:49-58.

［9］单德山，李乔，王玉珏.既有多梁式桥梁的损伤识别［J］.重庆交通大学学报:自然科学版，2008，27(7):5-8.

Shan Deshan，Li Qiao，Wang Yujue.Damage identification of existed multi-girders highway bridges［J］.Journal of Chongqing Jiaotong University:Natural Science，2008，27(7):5-8.

［10］刘基正，周志祥，陈波.桥梁损伤检测计算新方法探索［J］.重庆交通大学学报:自然科学版，2007，26(增刊1):25-27.

Liu Jizheng，Zhou Zhixiang，Chen Bo.Exploration of a new method to bridge detection calcualtion［J］.Journal of Chongqing Jiaotong University:Natural Science，2007，26(supp1):25-27.

Study on Two-Dimensional Damage Identification of T-Beam Based on Gaussian Curvature Mode Difference

Han Xi1，Li Qingda1，Zhong Li2，Yang Ke1
(1.School of Civil Engineering＆ Architecture，Chongqing Jiaotong University，Chongqing 400074，China;
2.School of Mechatronics＆ Automotive Engineering，Chongqing Jiaotong University，Chongqing 400074，China)

Curvature mode is a sensitive indicator to identify damage.Most researches on damage identification based on curvature mode are limited to one-dimensional structure.Damage identification based on Gaussian curvature mode was presented to extend curvature mode into two-dimensional structure，considering the degree of bending about two-dimensional structure of acceleration mode shape in the vertical level and horizontal level and locating the position of damage by calculating the Gaussian curvature difference of acceleration mode of structural damage on before and after.Mode test of the combination of T-beam structure and its results analysis show the feasibility of the proposed method.

Gaussian curvature;combination of T-beam structure;damage identification;two-dimensional identification

U441+.4

A

1674-0696(2012)04-0747-04

10.3969/j.issn.1674-0696.2012.04.03

2011-12-14;

2011-12-26

重庆市交通委员会科技项目(701487)

韩 西(1964—)，男，重庆人，教授，博士，主要从事结构力学、振动工程方面的研究。E-mail:xihan@cquc.edu.cn。