曲线钢箱梁多点横向顶推复位研究
2012-02-09江长森江凌乔
邓 娜,江长森,江凌乔
(1.成都理工大学 地球物理学院,四川 成都 610059;2.成都信息工程学院电子实验中心,四川成都 610225;
3.四川中水成勘院工程勘察有限责任公司,四川成都 610072;4.四川省邛崃市公路桥梁工程有限公司,四川邛崃 611530)
曲线钢箱梁多点横向顶推复位研究
邓 娜1,2,江长森3,江凌乔4
(1.成都理工大学 地球物理学院,四川 成都 610059;2.成都信息工程学院电子实验中心,四川成都 610225;
3.四川中水成勘院工程勘察有限责任公司,四川成都 610072;4.四川省邛崃市公路桥梁工程有限公司,四川邛崃 611530)
针对曲梁桥常出现的横向偏移现象,以某独墩单支座的曲线连续钢箱梁桥工程实例,采用通用有限元软件进行了仿真分析,针对曲梁桥的特点,采用竖向顶升和横向顶推相结合的复位方法,优化了顶推复位工序,确定了每点的顶(推)力计算方法。施工实践及运营情况表明,该复位方案合理、可靠。
曲线箱梁;复位施工;竖向顶推;横向顶推
0 引言
曲线梁桥在现代化的公路及城市道路立交中应用很普遍,特别是独墩单铰支座曲线梁桥。但是近几年来发现,这些曲线梁桥在运营过程中,出现了一些梁体滑移甚至翻转的桥梁事故。实际上,连续曲线箱梁桥在使用过程中,由于温度效应、车辆行驶或一些其它影响因素的作用,会产生侧向的变位[1]。由于曲梁的结构特点、支承形式等原因,当外荷载等影响因素消失后,曲梁发生的侧向变位并不能够完全恢复,弯梁在侧向会产生部分不可恢复的残余位移。长期反复作用下,侧向的残余位移就会累积,产生较大的位移,即曲线梁桥的侧向位移问题(国内有专家称之为“横向爬移”现象)。曲梁桥的侧向位移问题轻则导致梁段伸缩缝的剪切破坏,影响其使用寿命;严重的则会出现支承结构破坏、梁体滑移和翻转。如华强立交A匝道独柱曲线梁桥。
顶推施工[2]大量的应用于简支梁,连续梁桥,连续刚构桥等的架梁施工中,即用于梁顺桥向的顶推。在跨度较小的桥梁在发生过大横向位移以致威胁到安全运营时,也可以采用将梁顶起至滑道然后横向顶推至设计位置。这种横向顶推的方法已经在一些桥梁复位得到了应用,但应用于曲线梁的横向顶推施工研究还是比较少见的。由于曲线梁本身复杂的受力和变形性能,导致其在横向顶推施工中的复杂性将远大于直线梁。工程实践及理论[3]证明在顶推施工过程中对梁本身的受力行为影响不大,故笔者主要就已经发生横移危及运营,急需加固的曲线连续钢箱梁进行复位施工安全研究,通过分析横向顶推的施工顺序和施力大小得到优化的复位效果。
1 理论分析
由符拉索夫建立的薄壁圆弧平衡微分方程[4]可知:同直梁桥相比,曲线梁桥[5]的受力特性具有很大不同,即在荷载作用下曲线梁会产生强烈的挠曲扭转耦合反应,其平面弯曲变形是独立的,可以单独进行分析。研究发现,连续独墩单铰支座曲线箱梁桥的横移主要是其在平面内绕跨中固定铰支座旋转角度过大导致梁体滑移和翻转,故梁复位的关键是在不损害梁和墩正常使用性能的情况下使其回到设计位置[3]。由于梁体的变形、变位十分复杂,在3个方向6个自由度均存在不同程度变形、变位,因此梁的复位、校正是整个加固工程的关键。
梁的复位工作分为:顶升梁体;梁体平移;调整坡度;施工抗扭墩墩帽,更换支座;落梁就位,调整支座反力5个施工阶段(图1)。其关键的步骤就是竖向顶梁和水平顶推复位。在此过程中由于支点处约束条件的不同,梁将经历体系的转换。
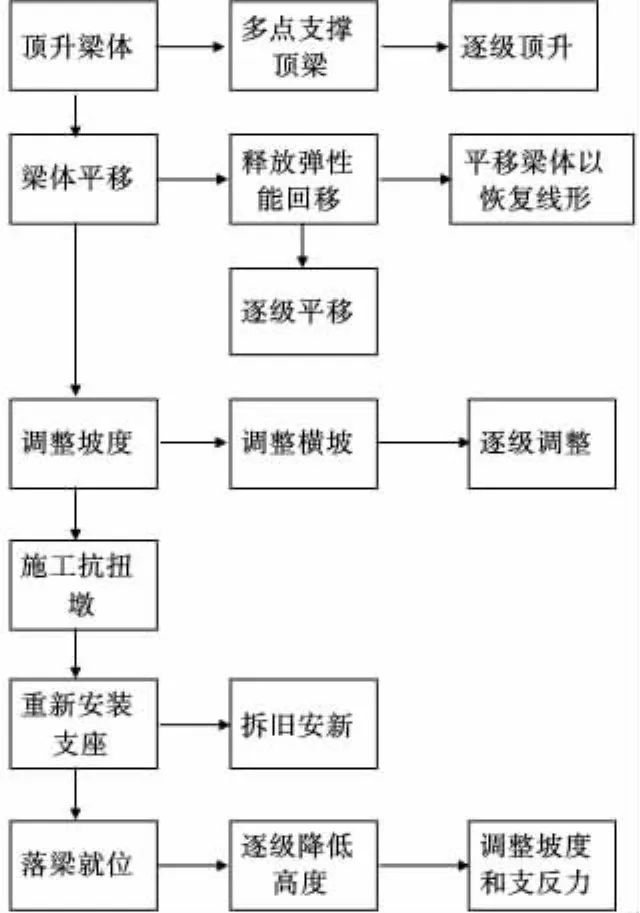
图1 曲线梁顶梁施工流程Fig.1 Processes of curve girder beam construction
1.1 顶梁分析
顶梁过程,即在搭建于既有墩处的临时墩上利用千斤顶将梁顶高离支座到一定高度[6]。对连续梁的顶梁主要有两种方式:多点同时顶起和逐墩顶起。前者主要针对直线梁,而对于曲线梁,由于在空间上梁还要受水平径向力,过大的水平径向力将使千斤顶破坏,采用哪种方式将取决于水平径向力[7]。
笔者将顶梁分为两个状态的迭加,即恒载和支反力共同作用下,向上位移为0的自平衡状态和向上竖向力顶起一段位移的上升状态的迭加。采用结构力学的方法,基于纯扭转理论单根曲线梁法[8]将常见的两端是抗扭支座,中间为点铰支承的N+1跨等截面连续曲线梁作为基本结构进行分析(图2),求出当支承i处有单位向上反力Ri=1作用下基本结构的挠度影响线,由此可得各支承点处的竖向位移wij,进而求得柔度矩阵[k]。

图2 中间为点铰支承的连续曲线梁Fig.2 Continuous curved beams of middle hinge supported
对向上竖向力顶起一段位移的上升状态,由力法原理可得典型方程:

式中:[k]为柔度矩阵;wij为支承j处作用单位支反力Rj=1时,支承i处的竖向位移;[R]为中间支承的竖向顶推力矩阵;[Δ]为各中间支承必需达到的竖向顶推高度矩阵。
考虑自平衡状态,由式(1)可得所需总竖向顶推力为:
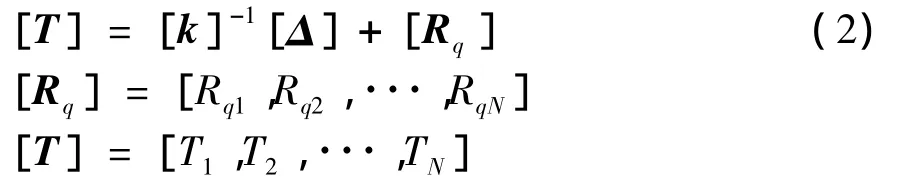
式中:[Rq]为在恒载作用下中间支承的竖向反力矩阵;[T]为中间支承的总竖向顶推力矩阵。
对两端抗扭支座,则可以利用悬臂曲线梁来计算其所需竖向顶推力大小。施工顺序将决定柔度矩阵,如果是逐墩顶起,柔度矩阵将是上三角矩阵,即当 i< j时,wij=0。
1.2 横向顶推梁分析
临时桥墩顶部设平台及横移梁滑道,在平台处设竖向千斤顶将梁体顶起一定高度后置于横移梁滑道上,再用横向千斤顶将已经脱离设计位置的梁体顶推到位。这个过程就是梁的横向顶推,也是复位施工成功的关键,必须综合分析各种因素的影响。当梁体处于滑道上时,梁体的扭转在该处被约束,此时结构已经演变成支承均为抗扭支座的连续曲线梁(图3)。一般认为横桥向的约束主要是摩擦力,这主要是根据直线梁的研究得到的,曲线梁由于恒载和温度荷载作用下在横桥向会产生附加横向力,特别是在跨中固定支座处的横向力是很大的,这在计算横向顶推力时是必须考虑的,即:

表1 恒载作用下横向力Table 1 Lateral force under constant load /kN
Ti=Hfi+Hi=μRqi+Hi(3)
式中:Ti为各支承的横向顶推力;Hfi为各支承处的摩擦力;Hi为各支承处由恒载和温度效应引起的附加横向力;μ为滑道摩擦系数。
2 工程实例分析
哈尔滨市某立交桥为六孔连续钢箱梁,总长221.342 m,钢箱梁跨径为 32.432 m+40 m+50 m+50 m+25 m+23.910 m,其中134.499 m 位于圆曲线上,曲线半径 R=85 m,α =89°20'20″。单箱三室钢箱梁截面底宽2.8 m,顶宽7.9 m,平均梁高1.5 m。设计荷载为城-A级车道荷载,桥面净空为净-7 m,双车道。钢箱梁G13、G19墩是抗扭支座,G14、G15、G17、G18 墩是多向盆式橡胶支座,G16墩固定盆式橡胶支座。
该立交桥于2000年10月竣工通车,运营1年后发现该桥连续钢箱梁出现横向偏移,2年后偏移增大。2002年6月测得偏移量:G19墩向曲线外侧偏移了120 mm,G13墩向曲线内侧偏移了100 mm,即连续钢箱梁绕G16墩出现了扭转现象。2004年8月测量发现:G19墩向曲线外侧偏移了245 mm,G13墩向曲线内侧偏移了150 mm,并有逐年加大趋势(图3)。另外 G17、G18墩偏移量达 350 mm[3]。

图3 原结构变形示意Fig.3 Deformation diagram of the original structure
实际工程中的曲线梁往往是曲直相连的,在理论上求解是非常困难的,一般采取数值方法。对于曲线箱梁一般可以将曲线梁简化成一根圆弧曲杆,采用分段空间直梁模型分析其受力特性,这种模型以空间直梁单元离散曲线梁,用分段的直线近似代替实际的曲线形式,模型自由度较少,计算工作量较小,在工程中得到广泛的应用。
利用大型专业软件MIDAS里空间梁单元建立有限元模型(图4),按照一般曲线钢梁制造工艺平均取1 m为一个单元,以直代曲,共117个单元。

图4 有限元模型Fig.4 Finite element model
2.1 顶梁过程分析
通过软件的计算,分别在中跨各墩处施加一单位力(取1kN),计算各墩的竖向位移,即可得曲线梁在不计恒载工况下的柔度矩阵[k],单位m。

由式(4)柔度矩阵可知曲线梁是很柔的结构,而顶起的位移[Δ]一般很小,取 5 cm,故[k]-1[Δ]≈0。由式(2)知:
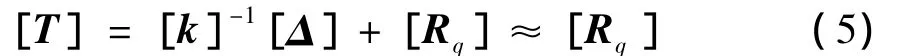
可见,在顶梁过程中只要按支反力来选取所需千斤顶即可。
由于曲梁在自重作用下会产生横向力,所以在顶起过程中,与直梁不同的是,千斤顶在承受竖向荷载同时将受到一个水平向的力。表1为恒载作用下横向力。
由表1可知:桥台支座和直梁端支座的横向力很小,而曲梁段固定支座如G16,承受的横向力最大。所以曲梁顶梁过程不能照搬直梁,必须逐墩逐级顶起,并作好横向固定工作,以免梁滑移造成事故。
由于顶起后梁需要一段时间释放弹性能,这段时间可能就会有温度变化,特别是在北方,昼夜温差大,而温度效应会产生横向力。通过分析各整桥温度分别升温10,20,30℃,降温10,20℃来研究温度效应对曲梁的横向力影响(表2),以力方向向圆弧内为正。

表2 温度荷载作用下横向力Table 2 Lateral force under temperature load /kN
由表2可知:温度作用引起的横向力要比恒载引起的小,而且随着温度升降而增减。
2.2 横向顶推过程分析
在曲梁逐步落到滑道上后,由于跨中G16墩为固定墩,该墩处位置没有改变,故横向顶推将推动梁以固定墩为中心转动到设计位置。在此过程中,一定要对固定墩进行加固,防止墩破坏。由于恒载会产生附加横向力,所以横向顶推力不能仅仅考虑摩擦力,还应加上附加横向力,表3为横向顶推力分析。按一般工程经验摩擦系数取0.1。

表3 横向顶推Table 3 Horizontal push /kN
通过对该桥的复位施工并对支座做相应的限位措施,经过几年运营未出现新问题,情况良好。
3 结论
1)通过对两个状态的迭加分析,对于大跨度大曲率曲梁桥在复位顶起施工过程中,由于结构很柔,竖向顶推力主要考虑支反力,并应采取逐墩顶推。
2)通过恒载,温度效应对顶起施工过程中曲梁横向力分析,发现横向力主要是由恒载产生,温度荷载影响较小。
3)在横向顶推过程中,横向顶推力必须同时考虑摩擦力和由恒载产生的附加横向力。
[1]张秋陵,黄超.小半径曲线箱梁桥预应力效应研究[J].重庆交通大学学报:自然科学版,2010,29(5):674-675.
Zhang Qiuling,Huang Chao.Study on effect of prestressed curved box girder bridge with small radius[J].Journal of Chongqing Jiaotong University:Natural Science,2010,29(5):674-675.
[2]周叶飞,龚静敏.变曲率竖曲线顶推施工钢箱梁局部受力分析[J].重庆交通大学学报:自然科学版,2010,29(3):355-357.
Zhou Yefei,Gong Jingmin.Curvature analysis of local stress for incremental launching construction of vertical curve changes steel box girder[J].Journal of Chongqing Jiaotong University:Natural Science,2010,29(3):355-357.
[3]王新丰.钢箱连续曲线梁桥横向复位技术的研究与实践[D].哈尔滨:哈尔滨工业大学,2007.
[4] 李乔.薄壁曲箱梁的空间分析理论[D].成都:西南交通大学,1988:5-29.
[5]朱强.小半径曲线叠合钢箱梁桥设计要点[J].山西建筑,2011(19):210-211.
Zhu Qiang.The design of small radius curved laminated steel box girder bridge[J].The construction in Shanxi province,2011(19):210-211.
[6]吴选涛,周志祥,曾凡江.曲线梁桥盖梁挡块裂缝分析[J].重庆交通大学学报:自然科学版,2008,27(1):1-4.
Wu Xuantao,Zhou Zhixiang,Zeng Fanjiang.Coping block crack analysis of curved beam bridge[J].Journal of Chongqing Jiaotong University:Natural Science,2008,27(1):1-4.
[7]向中富,卞明智,梁甜甜,等.曲梁在预应力径向分力作用下的受力分析[J].重庆交通大学学报:自然科学版,2008,27(6):5-6.
Xiang Zhongfu,Bian Mingzhi,Liang Tiantian,et al.Stress analysis of curved beam in pre-radial force[J].Journal of Chongqing Jiaotong University Natural Science,2008,27(6):5-6.
Deviation Reinforcement Analysis of Curved Steel Box Girder Bridge
Deng Na1,2,Jiang Changsen3,Jiang Lingqiao4
(1.College of Geophysics,Chengdu University of Technology,Chengdu 610059,Sichuan,China;
2.Electronic Laboratory,Chengdu University of Information Technology,Chengdu 610225,Sichuan,China;
3.Sichuan Hydropower Engineering Investigation Co.,Ltd.,Chengdu 610072,Sichuan,China;
4.Sichuan Highway and Bridge Engineering Co.,Ltd.,Qionglai 611530,Sichuan,China)
The creep deformations of curved girder bridge often occur.This paper makes a deviation rectifying research on lateral and torsional distortion of simple-supported continuous curved steel box girder bridge.By using FEM software MIDAS,the combined construction scheme of vertical and lateral thrusting is determined to rectify the curved beam.The construction process is optimized according to the characteristic of curved beam.Respectively methods are presented to caculate the thrusting force.The construction scheme is proved to be reasonable and practical in the practice.
curved box girder bridge;rectifying construction;vertical thrusting;lateral thrusting
U448.27
A
1674-0696(2012)04-0743-04
10.3969/j.issn.1674-0696.2012.04.02
2011-10-24;
2011-11-21
邓 娜(1980—),女,四川成都人,讲师,博士研究生,主要从事地球探测与信息技术、数字信号的智能处理等研究。E-mail:dn@cuit.edu.cn。
